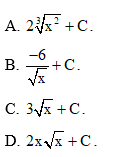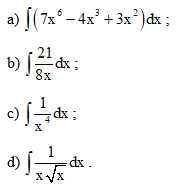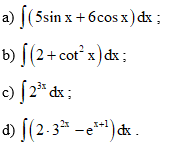Giải SGK Toán 12 Cánh Diều Bài 2: Nguyên hàm của một số hàm số sơ cấp

Câu hỏi khởi động: Một con lắc lò xo dao động điều hòa theo phương ngang trên mặt phẳng không ma sát như Hình 1, có vận tốc tức thời cho bởi v(t) = 4 cos t, trong đó t tính bằng giây và v(t) tính bằng centimét/giây. Tại thời điểm t = 0, con lắc đó ở vị trí cân bằng.

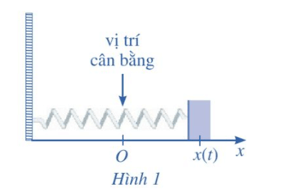
Phương trình chuyển động của con lắc đó được xác định bằng cách nào?

Lời giải:

I. Nguyên hàm của hàm số lũy thừa

Hoạt động 1: Hàm số F(x) = $\frac{1}{2}{x}^2$ có là nguyên hàm của hàm số f(x) = x hay không?

Lời giải:

Hàm số  là nguyên hàm của hàm số vì 

Luyện tập 1: Tìm: $\int \left(x^4-5x^2+1\right)dx$

Lời giải:

Ta có $\int \left(x^4-5x^2+1\right)dx=\int x^{4}dx-\int 5x^{2}dx+\int 1dx$

$=\frac{x^{4+1}}{4+1}-5\cdot \frac{x^{2+1}}{2+1}+x+C=\frac{x^5}{5}-\frac{5x^3}{3}+x+C$

Luyện tập 2: Tìm:

a) $\int x^{\frac{3}{5}}dx$;

b) $\int \frac{1}{\sqrt[4]{4x^3}}dx$

Lời giải:

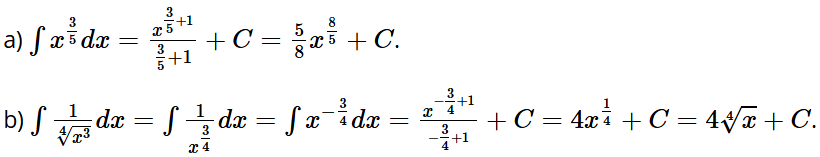
II. Nguyên hàm của hàm số lũy thừa f(x) = $\frac{1}{x}$

Hoạt động 2: 

a) Tính đạo hàm của hàm số y = ln|x| trên khoảng (0; + ∞).

b) Tính đạo hàm của hàm số y = ln|x| trên khoảng (– ∞; 0).

Lời giải:

a)   trên khoảng (0;+∞)

b)  trên khoảng (-∞;0)

Luyện tập 3: Tìm $\int \frac{4}{9x}dx$

Lời giải:

Ta có $\int \frac{4}{9x}dx=\frac{4}{9}\int \frac{1}{x}dx=\frac{4}{9}\ln \left|x\right|+C$

III. Nguyên hàm của hàm số lượng giác

Hoạt động 3: 

a) Hàm số y = – cos x có là nguyên hàm của hàm số y = sin x hay không?

b) Hàm số y = sin x có là nguyên hàm của hàm số y = cos x hay không?

c) Với x ≠ kπ (k ∈ ℤ), hàm số y = – cot x có là nguyên hàm của hàm số $y=\frac{1}{{\sin }^{2}x}$ hay không?

d) Với x ≠ $\frac{\pi }{2}$  + kπ (k ∈ ℤ), hàm số y = tan x có là nguyên hàm của hàm số $y=\frac{1}{{\cos }^{2}x}$  hay không?

Lời giải:

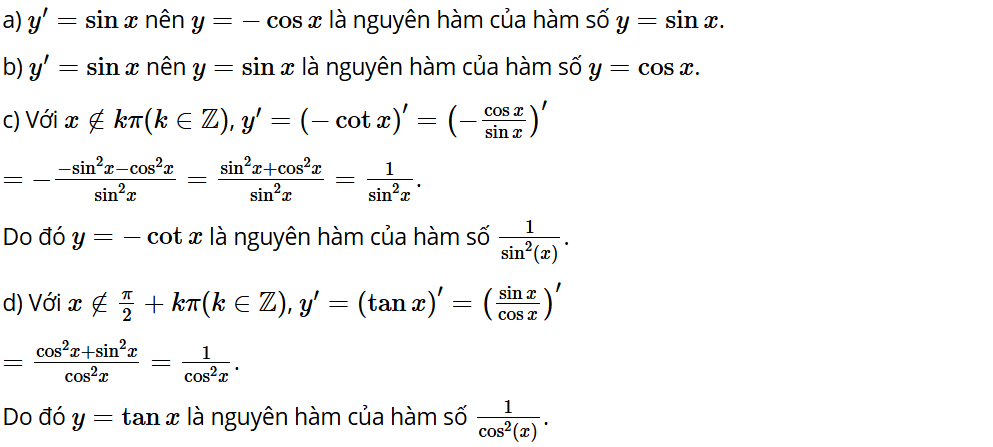
Luyện tập 4: Tìm:

a) $\int 8\sin xdx$

b) $\int \left(2\sin x-5\cos x\right)dx$

Lời giải:

a) $\int 8\sin xdx=8\int \sin xdx=8\cdot \left(-\cos x\right)+C=-8\cos x+C$

b) $\int \left(2\sin x-5\cos x\right)dx=\int 2\sin xdx-\int 5\cos xdx$

$=2\int \sin xdx-5\int \cos xdx=-2\cos x-5\sin x+C$

Luyện tập 5: Tìm:

a) $\int \left(1+{\cot }^{2}x\right)dx$

b) $\int \frac{1}{1+\cos 2x}dx$

Lời giải:

a)

b)

IV. Nguyên hàm của hàm số mũ

Hoạt động 4: Tính đạo hàm của hàm số $F\left(x\right)=\frac{a^x}{\ln a}$ (a > 0, a ≠ 1). Từ đó, nêu một nguyên hàm của hàm số f(x) = ax.

Lời giải:

Với a > 0, a ≠ 1, ta có $F^{\prime }\left(x\right)={\left(\frac{a^x}{\ln a}\right)}^{\prime }=\frac{1}{\ln a}{\left(a^x\right)}^{\prime }=\frac{1}{\ln a}\cdot \left(a^x\cdot \ln a\right)=a^x$ .

Vậy một nguyên hàm của hàm số f(x) = ax là $F\left(x\right)=\frac{a^x}{\ln a}$

Luyện tập 6: Tìm:

a) $\int 4^{x+2}dx$

b) $\int \left(5^{x+2}-e^{x+1}\right)dx$

Lời giải:

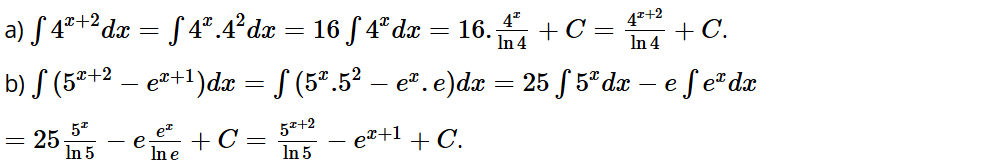
Bài tập

Bài tập 1: $\int \left(2\sin x-3\cos x\right)dx$ bằng:

A. 2cos x – 3sin x + C.

B. 2cos x + 3sin x + C.

C. – 2cos x + 3sin x + C.

D. – 2cos x – 3sin x + C.

Đáp án: D

Ta có $\int \left(2\sin x-3\cos x\right)dx=2\int \sin xdx-3\int \cos xdx=-2\cos x-3\sin x+C$

Bài tập 2: $\int 7^{x}dx$ bằng:

A. 7x ∙ ln7 + C.

B. $\frac{7^{x+1}}{x+1}+C$.

C. $\frac{7^x}{\ln 7}+C$.

D. 7x + C.

Đáp án: C

Bài tập 3: Nguyên hàm của hàm số $f\left(x\right)=\frac{3x}{\sqrt{x}}$ bằng:

Đáp án: D

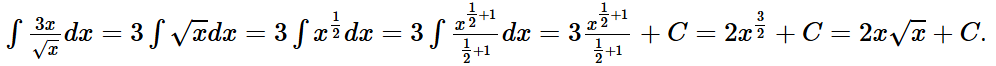
Bài tập 4: Nguyên hàm của hàm số f(x) = 1 – tan2 x bằng:

A. 2 – tan x + C.

B. 2x – tan x + C.

C. $x-\frac{{\tan }^{3}x}{3}+C$.

D. – 2 tan x + C.

Đáp án: B

Ta có $\int \left(1-{\tan }^{2}x\right)dx=\int \left[2-\left(1+{\tan }^{2}x\right)\right]dx$$=\int \left(2-\frac{1}{{\cos }^{2}x}\right)dx$

$=\int 2dx-\int \frac{1}{{\cos }^{2}x}dx$= 2x – tan x + C.

Bài tập 5: Tìm:

Lời giải:

a)

b)

c)

d)

Bài tập 6: Tìm:

Lời giải:

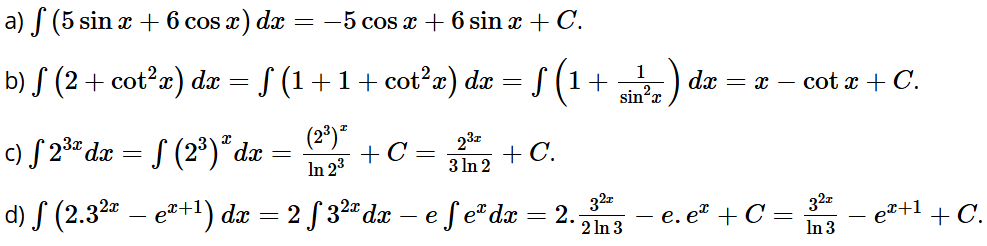
Bài tập 7: Cây cà chua khi trồng có chiều cao 5 cm. Tốc độ tăng chiều cao của cây cà chua sau khi trồng được cho bởi hàm số

v(t) = – 0,1t3 + t2,

trong đó t tính theo tuần, v(t) tính bằng centimét/tuần. Gọi h(t) (tính bằng centimét) là độ cao của cây cà chua ở tuần thứ t (Nguồn: A. Bigalke et aL, Mathematik, Grundkurs ma-1, Cornelsen 2016).

a) Viết công thức xác định hàm số h(t) (t ≥ 0).

b) Giai đoạn tăng trưởng của cây cà chua đó kéo dài bao lâu?

c) Chiều cao tối đa của cây cà chua đó là bao nhiêu centimét?

d) Vào thời điểm cây cà chua đó phát triển nhanh nhất thì cây cà chua cao bao nhiêu centimét?

Lời giải:

a) Hàm số h(t) là một nguyên hàm của hàm số v(t).

Ta có $\int v\left(t\right)dt=\int \left(-0,1t^3+t^2\right)dt=-0,1\int t^{3}dt+\int t^{2}dt=-0,025t^4+\frac{t^3}{3}+C$ .

Suy ra $h\left(t\right)=-0,025t^4+\frac{t^3}{3}+C$ .

Vì cây cà chua khi trồng có chiều cao 5 cm nên h(0) = 5, suy ra C = 5.

Vậy công thức xác định hàm số h(t) là: $h\left(t\right)=-0,025t^4+\frac{t^3}{3}+5\left(t\ge 0\right)$ .

b) Xét hàm số $h\left(t\right)=-0,025t^4+\frac{t^3}{3}+5\left(t\ge 0\right)$ .

Ta có h'(t) = v(t) = – 0,1t3 + t2; h'(t) = 0 khi t = 0 hoặc t = 10.

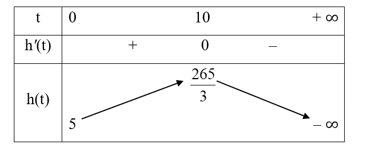
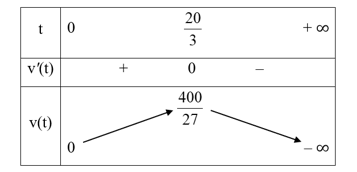
Bảng biến thiên của hàm số h(t) trên [0; + ∞) như sau:

Từ bảng biến thiên ta thấy giai đoạn tăng trưởng của cây cà chua đó kéo dài 10 tuần.

c) Từ bảng biến thiên ở câu b, ta thấy chiều cao tối đa của cây cà chua đó là $\frac{265}{3}$  cm.

d) Xét hàm tốc độ tăng chiều cao của cây cà chua: v(t) = – 0,1t3 + t2 (t ≥ 0).

Ta có v'(t) = – 0,3t2 + 2t; v'(t) = 0 khi t = 0 hoặc t = $\frac{20}{3}$ .

Bảng biến thiên của hàm số v(t) trên [0; + ∞) như sau:

Từ bảng biến thiên ta suy ra vào thời điểm cây cà chua đó phát triển nhanh nhất thì cây cà chua cao $\frac{400}{27}$ cm.

Bài tập 8: Một quần thể vi khuẩn ban đầu gồm 500 vi khuẩn, sau đó bắt đầu tăng trưởng. Gọi P(t) là số lượng vi khuẩn của quần thể đó tại thời điểm t, trong đó t tính theo ngày (0 ≤ t ≤ 10). Tốc độ tăng trưởng của quần thể vi khuẩn đó cho bởi hàm số P'(t) = $k\sqrt{t}$, trong đó k là hằng số. Sau 1 ngày, số lượng vi khuẩn của quần thể đó đã tăng lên thành 600 vi khuẩn (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014). Tính số lượng vi khuẩn của quần thể đó sau 7 ngày (làm tròn kết quả đến hàng đơn vị).

Lời giải:

Số lượng vi khuẩn tăng trưởng sẽ được tính bởi hàm P(t), với P(t) là nguyên hàm của hàm P’(t):

Điều kiện ban đầu P(0)=500: 

C=500

Sau 1 ngày, số lượng vi khuẩn tăng thành 600:

Ta có hàm P(t): 

Sau 7 ngày, số lượng vi khuẩn là: 

Vậy số lượng vi khuẩn sau 7 ngày là 2352 vi khuẩn.