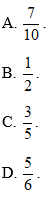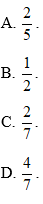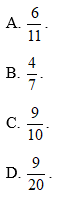Giải SGK Toán 12 Cánh Diều Bài 1: Xác xuất có điều kiện

Câu hỏi khởi động: Một lớp học có 17 học sinh nữ và 13 học sinh nam. Ở lớp học đó, có 3 học sinh tên là Thanh, trong đó có 1 học sinh nữ và 2 học sinh nam. Thầy giáo gọi ngẫu nhiên một học sinh lên bảng. Xét hai biến cố sau:

A: “Học sinh được gọi lên bảng có tên là Thanh”;

B: “Học sinh được gọi lên bảng là học sinh nữ”.

Xác suất của biến cố A với điều kiện biến cố B đã xảy ra được tính như thế nào?

Lời giải:

I. Định nghĩa xác suất có điều kiện

Hoạt động 1: Trong bài toán ở phần mở đầu, hãy tính:

a) Xác suất để học sinh được gọi lên bảng có tên là Thanh, biết rằng học sinh đó là nữ;

b) Tính tỉ số $\frac{P\left(A\cap B\right)}{P\left(B\right)}$. Từ đó, hãy so sánh xác suất tính được ở câu a) với tỉ số $\frac{P\left(A\cap B\right)}{P\left(B\right)}$

Lời giải:

a) 

Ta có: Số học sinh nữ là 17, trong đó có 1 học sinh nữ tên Thanh

Xác suất học sinh được gọi lên bảng có tên là Thanh, biết rằng học sinh đó là nữ là: 

b) Ta có các biến cố

A: “Học sinh được gọi lên bảng có tên là Thanh";

B: “Học sinh được gọi lên bảng là học sinh nữ”.

Ta có:

 (số học sinh nữ)

(số học sinh nữ tên Thanh)

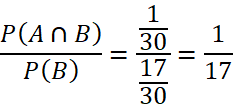
Vậy tỷ số  bằng với kết quả thu được ở câu A.

Luyện tập 1: Một hộp có 6 quả bóng màu xanh, 4 quả bóng màu đỏ; các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên lần lượt hai quả bóng trong hộp, lấy không hoàn lại. Tìm xác suất để lần thứ hai lấy được quả bóng màu đỏ, biết rằng lần thứ nhất đã lấy được quả bóng màu xanh.

Lời giải:

Xét hai biến cố sau:

A: “Lần thứ hai lấy được quả bóng màu đỏ”;

B: “Lần thứ nhất lấy được quả bóng màu xanh”.

Khi đó, xác suất để lần thứ hai lấy được quả bóng màu đỏ, biết rằng lần thứ nhất đã lấy được quả bóng màu xanh, chính là xác suất của A với điều kiện B.

Cách 1:

Nếu B xảy ra, tức là lần thứ nhất lấy được quả bóng màu xanh. Khi đó, trong hộp còn lại 9 quả bóng với 5 quả bóng màu xanh và 4 quả bóng màu đỏ.

Vậy xác suất để lần thứ hai lấy được quả bóng màu đỏ, biết rằng lần thứ nhất đã lấy được quả bóng màu xanh là: P(A | B) = $\frac{4}{9}$ .

Cách 2:

Lấy ngẫu nhiên lần lượt hai quả bóng trong hộp, lấy không hoàn lại, lần thứ nhất lấy một quả bóng có 10 cách chọn, lần thứ hai lấy một quả bóng có 9 cách chọn một quả bóng trong hộp. Do đó, n(Ω) = 10 ∙ 9 = 90.

Lần thứ nhất lấy bóng có 6 cách chọn một quả bóng màu xanh, lần thứ hai có 9 cách chọn một quả bóng từ 9 quả bóng còn lại trong hộp. Do đó, n(B) = 6 ∙ 9 = 54.

Khi đó, P(B) = $\frac{54}{90}=\frac{3}{5}$ .

Lần thứ nhất lấy bóng có 6 cách chọn một quả bóng màu xanh, lần thứ hai lấy bóng có 4 cách chọn một quả bóng màu đỏ. Do đó, n(A ∩ B) = 6 ∙ 4 = 24.

Khi đó, P(A ∩ B) = $\frac{24}{90}=\frac{4}{15}$ .

Vậy xác suất để lần thứ hai lấy được quả bóng màu đỏ, biết rằng lần thứ nhất đã lấy được quả bóng màu xanh là:

P(A | B) =$\frac{P\left(A\cap B\right)}{P\left(B\right)}=\frac{\frac{4}{15}}{\frac{3}{5}}=\frac{4}{9}$

Luyện tập 2: Trong hộp đựng 500 chiếc thẻ cùng loại có 200 chiếc thẻ màu vàng. Trên mỗi chiếc thẻ màu vàng có ghi một trong năm số: 1, 2, 3, 4, 5. Có 40 chiếc thẻ màu vàng ghi số 5. Chọn ra ngẫu nhiên một chiếc thẻ trong hộp đựng thẻ. Giả sử chiếc thẻ được chọn ra có màu vàng. Tính xác suất để chiếc thẻ đó ghi số 5.

Lời giải:

Xét 2 biến cố:

- A : "Chiếc thẻ được chọn có màu vàng".

- B: "Chiếc thẻ được chọn ghi số 5".

Xác suất để chiếc thẻ đó ghi số 5, biết rằng chiếc thẻ đó có màu vàng là xác suất của biến cố B với điều kiện A.

Ta có 200 thẻ màu vàng trên 500 thẻ. Xác suất để chọn được một chiếc thẻ màu vàng:

Có 40 thẻ màu vàng ghi số 5 trên tổng 500 thẻ. Xác suất để chọn được một chiếc thẻ màu vàng ghi số 5:

Xác suất để chiếc thẻ đó ghi số 5, biết rằng chiếc thẻ đó có màu vàng:

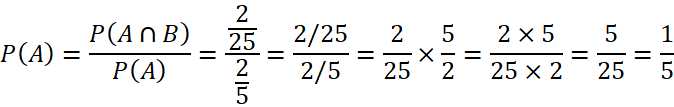
Vậy, xác suất để chiếc thẻ đó ghi số 5, biết rằng chiếc thẻ đó có màu vàng, là 

Luyện tập 3: Với các giả thiết như ở Ví dụ 4, chọn ngẫu nhiên một người trong số những người thử nghiệm. Tính xác suất để người được chọn ra bị nhiễm bệnh sốt xuất huyết, biết rằng người đó có kết quả thử nghiệm âm tính (làm tròn kết quả đến hàng phần mười).

Lời giải:

II. Sử dụng sơ đồ hình cây để tính xác suất có điều kiện

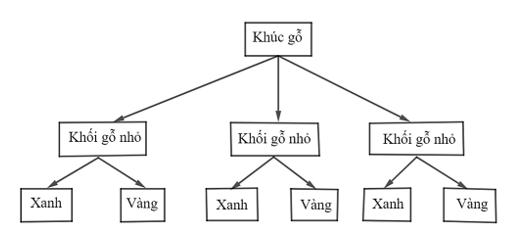
Hoạt động 2: Bác An cưa một khúc gỗ thành ba khối nhỏ. Mỗi khối nhỏ được sơn bằng một trong hai màu xanh hoặc vàng. Vẽ sơ đồ hình cây biểu thị các khả năng mà bác An có thể sơn màu cho khúc gỗ đó.

Lời giải:

Ta vẽ sơ đồ hình cây như sau:

Luyện tập 4: Một túi có 10 hộp sữa chua dâu và 10 hộp sữa chua nha đam; các hộp sữa chua có kích thước và khối lượng như nhau. Có 12 hộp sữa chua trong túi là sữa chua không đường, trong đó có 6 hộp sữa chua dâu và 6 hộp sữa chua nha đam. Lấy ngẫu nhiên một hộp sữa chua trong túi. Dùng sơ đồ hình cây, tính xác suất để hộp sữa chua được lấy ra là hộp sữa chua dâu, biết rằng hộp sữa chua đó là sữa chua không đường.

Lời giải:

Xét các biến cố:

A: Lấy được sữa chua có đường

B: Lấy được sữa chua không đường

C: Lấy được sữa chua dâu

D: Lấy được sữa chua nha đam

Ta có sơ đồ cây:

Xác suất hộp sữa chua được lấy ra là hộp sữa chua dâu, biết rằng hộp sữa chua đó là sữa chua không đường là 0,5.

Bài tập

Bài tập 1: Cho hai biến cố độc lập A, B với P(A) = 0,8, P(B) = 0,25. Khi đó, P(A | B) bằng:

A. 0,2.

B. 0,8.

C. 0,25.

D. 0,75.

Đáp án: B

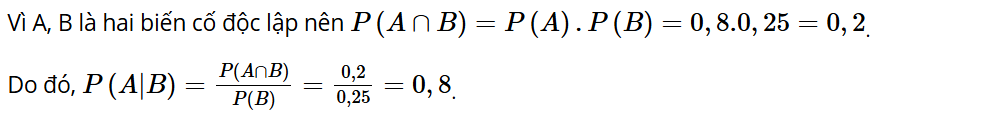
Bài tập 2: Trong một khu phố có 100 nhà, tại đó có 60 nhà gắn biển số chẵn và 40 nhà gắn biển số lẻ. Bên cạnh đó, có 50 nhà gắn biển số chẵn và 20 nhà gắn biển số lẻ đều có ô tô. Chọn ngẫu nhiên một nhà trong khu phố đó.

a) Xác suất nhà được chọn có ô tô, biết rằng nhà đó gắn biển số chẵn, là:

b) Xác suất nhà được chọn gắn biển số lẻ, biết rằng nhà đó có ô tô, là:

Lời giải:

a) Đáp án: D

Xét hai biến cố:

A: “Nhà được chọn có ô tô”;

B: “Nhà được chọn gắn biển số chẵn”.

Khi đó, xác suất nhà được chọn có ô tô, biết rằng nhà đó gắn biển số chẵn, chính là xác suất có điều kiện P(A | B).

Theo bài ra, ta có: $P\left(B\right)=\frac{60}{100}=0,6$; $P\left(A\cap B\right)=\frac{50}{100}=0,5$ .

Khi đó, P(A | B) = $\frac{P\left(A\cap B\right)}{P\left(B\right)}=\frac{0,5}{0,6}=\frac{5}{6}$

b) Đáp án: A.

Gọi C là biến cố nhà được chọn có ô tô, L là biến cố nhà được chọn gắn biển số lẻ.

Ta có:

Vì A và B độc lập, nên ta có: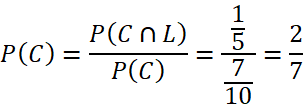 

Bài tập 3: Một phòng học môn Tin học có 40 máy tính được đánh số từ 1 đến 40, các máy cùng loại và cùng màu, mỗi máy được đánh một số khác nhau. Trong phòng học đó, xác suất chọn được một máy tính đã cài đặt phần mềm lập trình Python được đánh số chẵn và được đánh số lẻ lần lượt là 0,375 và 0,45. Bạn Nam chọn ngẫu nhiên một máy tính trong phòng học đó.

a) Xác suất bạn Nam chọn được máy tính đã cài đặt phần mềm lập trình Python, biết rằng máy tính đó được đánh số lẻ, là:

b) Xác suất bạn Nam chọn được máy tính đánh số chẵn, biết rằng máy tính đó đã cài đặt phần mềm lập trình Python, là:

Lời giải:

a)

Gọi A là biến cố bạn Nam chọn được máy tính đã cài đặt phần mềm lập trình Python, B là biến cố máy tính được đánh số lẻ.

Theo đề bài, ta có:

 Xác suất bạn Nam chọn được máy tính đã cài đặt phần mềm lập trình Python, biết rằng máy tính đó được đánh số lẻ, là: 

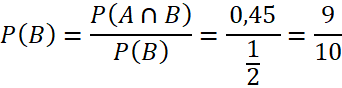
Đáp án C.

b) Gọi C là biến cố máy tính được đánh số chẵn.

Theo đề bài, ta có:

Xác suất bạn Nam chọn được máy tính đánh số chẵn, biết rằng máy tính đó đã cài đặt phần mềm lập trình Python, là: 

Đáp án B.

Bài tập 4: Cho hai biến cố A, B có P(A) = 0,6; P(B) = 0,8; P(A ∩ B) = 0,4. Tính các xác suất sau:

a) P(B | A);

b) P(A ∩ $\overline{B}$);

c) P( $\overline{B}$ | A).

Lời giải:

a) Ta có P(B | A) = $\frac{P\left(A\cap B\right)}{P\left(A\right)}=\frac{0,4}{0,6}=\frac{2}{3}$.

b) Vì A ∩ $\overline{B}$ và A ∩ B là hai biến cố xung khắc và (A ∩ $\overline{B}$ ) ∪ (A ∩ B) = A nên theo tính chất của xác suất ta có P(A) = P(A ∩ $\overline{B}$ ) + P(A ∩ B).

Suy ra P(A ∩ $\overline{B}$ ) = P(A) – P(A ∩ B) = 0,6 – 0,4 = 0,2.

c) Ta có c) Ta có P( $\overline{B}$ | A) = $\frac{P\left(\overline{B}\cap A\right)}{P\left(A\right)}=\frac{P\left(A\cap \overline{B}\right)}{P\left(A\right)}=\frac{0,2}{0,6}=\frac{1}{3}$

Bài tập 5: Một hộp có 3 quả bóng màu xanh, 4 quả bóng màu đỏ; các quả bóng có kích thước và khối lượng như nhau. Lấy bóng ngẫu nhiên hai lần liên tiếp, trong đó mỗi lần lấy ngẫu nhiên một quả bóng trong hộp, ghi lại màu của quả bóng lấy ra và bỏ lại quả bóng đó vào hộp. Xét các biến cố:

A: “Quả bóng màu xanh được lấy ra ở lần thứ nhất”;

B: “Quả bóng màu đỏ được lấy ra ở lần thứ hai”.

Chứng minh rằng A, B là hai biến cố độc lập.

Lời giải:

Xác suất của biến cố A:

 A là biến cố "Quả bóng màu xanh được lấy ra ở lần thứ nhất".

Số quả bóng xanh trong hộp là 3 và tổng số quả bóng là 7. Vậy xác suất lấy được quả bóng xanh ở lần thứ nhất là: 

B là biến cố "Quả bóng màu đỏ được lấy ra ở lần thứ hai".

Số quả bóng đỏ trong hộp là 4 và tổng số quả bóng là 7. Vậy xác suất lấy được quả bóng đỏ ở lần thứ hai là: 

Biến cố  là biến cố "Quả bóng màu xanh được lấy ra ở lần thứ nhất và quả bóng màu đỏ được lấy ra ở lần thứ hai". 

Mà ta có: 

Do  nên hai biến cố A và B là độc lập.

Bài tập 6: Cho hai xúc xắc cân đối và đồng chất. Gieo lần lượt từng xúc xắc trong hai xúc xắc đó. Tính xác suất để tổng số chấm xuất hiện trên hai xúc xắc bằng 6, biết rằng xúc xắc thứ nhất xuất hiện mặt 4 chấm.

Lời giải:

Bài tập 7: Một doanh nghiệp trước khi xuất khẩu áo sơ mi trong lô hàng S phải qua hai lần kiểm tra chất lượng sản phẩm, nếu cả hai lần đều đạt thì chiếc áo trong lô hàng đó mới đủ tiêu chuẩn xuất khẩu. Biết rằng bình quân 98% sản phẩm làm ra qua được lần kiểm tra thứ nhất và 95% sản phẩm qua được lần kiểm tra thứ nhất sẽ tiếp tục qua được lần kiểm tra thứ hai. Chọn ra ngẫu nhiên một chiếc áo sơ mi trong lô hàng S. Tính xác suất để một chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu.

Lời giải:

Gọi A là biến cố: “chiếc áo sơ mi trong lô hàng S được chọn qua được lần kiểm tra thứ nhất”, B là biến cố: “chiếc áo sơ mi trong lô hàng S được chọn qua được lần kiểm tra thứ hai”, C là biến cố: “chiếc áo sơ mi được chọn đủ tiêu chuẩn xuất khẩu”.

Theo bài ra ta có: P(A) = 98% = 0,98; P(B | A) = 95% = 0,95.

Một chiếc áo đủ tiêu chuẩn xuất khẩu khi cả hai lần kiểm tra chất lượng sản phẩm đều đạt. Xác suất để một chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu là:

P(C) = P(A) ∙ P(B | A) = 0,98 ∙ 0,95 = 0,931.

Bài tập 8: Một lô sản phẩm có 20 sản phẩm, trong đó có 5 sản phẩm chất lượng thấp. Lấy liên tiếp 2 sản phẩm trong lô sản phẩm trên, trong đó sản phẩm lấy ra ở lần thứ nhất không được bỏ lại vào lô sản phẩm. Tính xác suất để cả hai sản phẩm được lấy ra đều có chất lượng thấp.

Lời giải:

Xét 2 biến cố:

- A: Biến cố "sản phẩm lấy ra lần thứ nhất có chất lượng thấp".

- B: Biến cố "sản phẩm lấy ra lần thứ hai có chất lượng thấp".

Xác suất để cả hai sản phẩm được lấy ra đều có chất lượng thấp, tức là 

Xác suất để lấy ra một sản phẩm chất lượng thấp ở lần lấy thứ nhất là: 

Nếu sản phẩm đầu tiên đã được lấy ra và nó có chất lượng thấp, thì số sản phẩm còn lại trong lô là 19, trong đó có 4 sản phẩm chất lượng thấp. Xác suất để lấy ra một sản phẩm chất lượng thấp ở lần lấy thứ hai, với điều kiện lần đầu đã lấy ra một sản phẩm chất lượng thấp, là: 

Xác suất để cả hai sản phẩm lấy ra đều có chất lượng thấp là:

Vậy xác suất để cả hai sản phẩm được lấy ra đều có chất lượng thấp là khoảng 0.0526, hay 5.26%. 

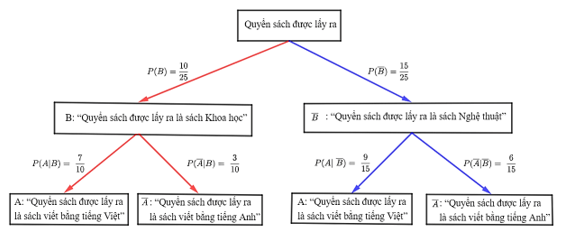
Bài tập 9: Trên giá sách có 10 quyển sách Khoa học và 15 quyển sách Nghệ thuật. Có 9 quyển sách viết bằng tiếng Anh, trong đó 3 quyển sách Khoa học và 6 quyển sách Nghệ thuật, các quyển sách còn lại viết bằng tiếng Việt. Lấy ngẫu nhiên một quyển sách. Dùng sơ đồ hình cây, tính xác suất để quyển sách được lấy ra là sách viết bằng tiếng Việt, biết rằng quyển sách đó là sách Khoa học.

Lời giải:

Vì có 9 quyển sách viết bằng tiếng Anh, trong đó 3 quyển sách Khoa học và 6 quyển sách Nghệ thuật, các quyển sách còn lại viết bằng tiếng Việt nên ta có:

10 + 15 – 9 = 16 quyển sách viết bằng tiếng Việt,

trong đó có 10 – 3 = 7 quyển sách Khoa học và 15 – 6 = 9 quyển sách Nghệ thuật.

Xét hai biến cố sau:

A: “Quyển sách được lấy ra là sách viết bằng tiếng Việt”;

B: “Quyển sách được lấy ra là sách Khoa học”.

Khi đó, xác suất để quyển sách được lấy ra là sách viết bằng tiếng Việt, biết rằng quyển sách đó là sách Khoa học, chính là xác suất có điều kiện P(A | B).

Sơ đồ hình cây biểu thị cách tính xác suất có điều kiện P(A | B), được vẽ như sau:

Vậy xác suất để quyển sách được lấy ra là sách viết bằng tiếng Việt, biết rằng quyển sách đó là sách Khoa học, là $\frac{7}{10}$ = 0,7.