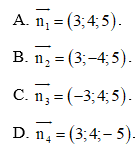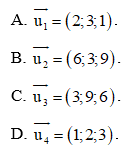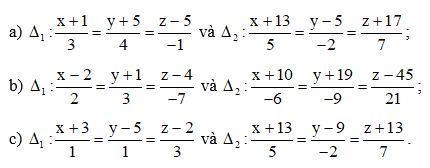Giải SGK Toán 12 Cánh Diều Bài tập cuối chương V - Giải SGK Toán 12 - Cánh Diều

Bài tập 1: Mặt phẳng (P): 3x – 4y + 5z – 6 = 0 có một vectơ pháp tuyến là:

Bài 1 trang 87 Toán 12 Cánh diều Tập 2 | Giải Toán 12

Đáp án: B

Mặt phẳng (P): 3x – 4y + 5z – 6 = 0 có một vectơ pháp tuyến là: $\vec{n} = (3; - 4; 5)$

Bài tập 2: Đường thẳng $d : \frac{x - 2}{3} = \frac{y - 3}{6} = \frac{z - 1}{9}$ có một vectơ chỉ phương là:

Bài 2 trang 87 Toán 12 Cánh diều Tập 2 | Giải Toán 12

Đáp án: D

Đường thẳng có một vectơ chỉ phương là:

Bài tập 3:

a) Mặt cầu (S): (x – 11)2 + (y – 12)2 + (z – 13)2 = 100 có bán kính là:

A. 10.

B. 11.

C. 12.

D. 13.

b) Tọa độ tâm của mặt cầu (S): (x – 5)2 + (y + 6)2 + (z – 7)2 = 8 là:

A. (5; 6; 7).

B. (5; 6; – 7).

C. (5; – 6; 7).

D. (– 5; 6; 7).

a) Đáp án: A

Mặt cầu (S): (x – 11)2 + (y – 12)2 + (z – 13)2 = 100 có bán kính là $R = \sqrt{100} = 10$ .

b) Đáp án: C

Ta có (x – 5)2 + (y + 6)2 + (z – 7)2 = 8 ⇔ (x – 5)2 + [y – (– 6)]2 + (z – 7)2 = 8.

Vậy tọa độ tâm của mặt cầu (S) là (5; – 6; 7).

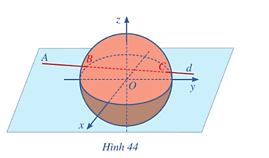
Bài tập 4: Khoảng cách từ điểm M(a; b; c) đến mặt phẳng x – a – b – c = 0 là:

A. |a + b|.

B. |b + c|.

C. |c + a|.

D. $\frac{|b + c|}{\sqrt{a^{2} + b^{2} + c^{2}}}$ .

Đáp án: B

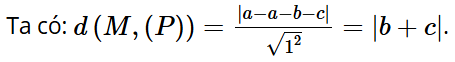
Bài tập 5: Cho bốn điểm A(0; 1; 3), B(– 1; 0; 5), C(2; 0; 2) và D(1; 1; – 2).

a) Tìm toạ độ của hai vectơ $\vec{A B}, \vec{A C}$ và một vectơ vuông góc với cả hai vectơ đó.

b) Viết phương trình tham số và phương trình chính tắc của hai đường thẳng AB và AC.

c) Viết phương trình tổng quát của mặt phẳng (ABC).

d) Chứng minh rằng bốn điểm A, B, C, D không đồng phẳng.

e) Tính khoảng cách từ điểm D đến mặt phẳng (ABC).

Lời giải:

Bài tập 6: Viết phương trình tổng quát của mặt phẳng (P) trong mỗi trường hợp sau:

a) (P) đi qua điểm M(– 3; 1; 4) và có một vectơ pháp tuyến là $\vec{n} = (2; - 4; 1)$ ;

b) (P) đi qua điểm N(2; – 1; 5) và có cặp vectơ chỉ phương là $\vec{u_{1}} = (1; - 3; - 2)$ và $\vec{u_{2}} = (- 3; 4; 1)$ ;

c) (P) đi qua điểm I(4; 0; – 7) và song song với mặt phẳng (Q): 2x + y – z – 3 = 0;

d) (P) đi qua điểm K(– 4; 9; 2) và vuông góc với đường thẳng $Δ : \frac{x - 1}{2} = \frac{y}{1} = \frac{z - 6}{5}$

Lời giải:

a) Phương trình mặt phẳng (P) đi qua điểm M(-3;1;4) và có một vectơ pháp tuyến là

b) Tính vector pháp tuyến của mặt phẳng (P):

Phương trình mặt phẳng (P) là:

c) Nếu (P) song song với (Q), thì chúng có cùng vectơ pháp tuyến (2; 1; -1).

Phương trình mặt phẳng (P) là:

d) Vectơ chỉ phương của đường thẳng là (2; 1; 5), nên vectơ pháp tuyến của mặt phẳng (P) là (2; 1; 5) do

Phương trình mặt phẳng (P) là:

Bài tập 7: Viết phương trình của mặt cầu (S) trong mỗi trường hợp sau:

a) (S) có tâm I(4; – 2; 1) và bán kính R = 9;

b) (S) có tâm I(3; 2; 0) và đi qua điểm M(2; 4; – 1);

c) (S) có đường kính là đoạn thẳng AB với A(1; 2; 0) và B(– 1; 0; 4).

Lời giải:

a) Phương trình mặt cầu (S) có tâm I(4; – 2; 1) và bán kính R = 9 là:

(x – 4)2 + (y + 2)2 + (z – 1)2 = 81.

b) Ta có bán kính của mặt cầu (S) là R = IM = $\sqrt{{(2 - 3)}^{2} + {(4 - 2)}^{2} + {(- 1 - 0)}^{2}} = \sqrt{6}$ .

Phương trình mặt cầu (S) là:

(x – 3)2 + (y – 2)2 + z2 = 6.

c) Tâm của mặt cầu (S) là trung điểm I của đoạn thẳng AB.

Ta có $x_{I} = \frac{1 + (- 1)}{2} = 0; y_{I} = \frac{2 + 0}{2} = 1; z_{I} = \frac{0 + 4}{2} = 2$ . Suy ra I(0; 1; 2).

Bán kính của mặt cầu (S) là R = IA = $\sqrt{{(1 - 0)}^{2} + {(2 - 1)}^{2} + {(0 - 2)}^{2}} = \sqrt{6}$ .

Phương trình mặt cầu (S) là:

x2 + (y – 1)2 + (z – 2)2 = 6.

Bài tập 8: Xác định vị trí tương đối của hai đường thẳng ∆1 và ∆2 trong mỗi trường hợp sau:

Bài 8 trang 88 Toán 12 Cánh diều Tập 2 | Giải Toán 12

Lời giải:

Vectơ chỉ phương của là

Ta xét tỉ lệ:

và không tỉ lệ

Phương trình tham số của

Cho

Ta có:

Thay t vào các phương trình còn lại:

Hệ phương trình có 1 nghiệm (t;s)=(1;3). Vậy 2 đường thẳng cắt nhau.

Vectơ chỉ phương củalà

Vectơ chỉ phương của là

Xét tỉ lệ:

và tỉ lệ với nhau. Xét điểm (2;-1;4) thuộc . Thay vào :

Vậy 2 đường thẳng song song.

Vectơ chỉ phương của là

Xét 2 tỉ lệ: và không tỉ lệ

Xét:

Điểm trên

Cho

Từ phương trình đầu tiên, ta có:

Từ phương trình thứ 2, ta có:

Cho (1)=(2)

Thay s vào phương trình 2:

Thay s vào phương trình 1:

Phương trình 1 mâu thuẫn với phương trình 2

Hệ phương trình không có nghiệm, do vậy 2 đường chéo nhau.

Bài tập 9: Tìm góc giữa hai đường thẳng ∆1 và ∆2, biết $Δ_{1} : \{\begin{cases} x = 1 + t_{1} \\ y = 2 - \sqrt{2} t_{1} \\ z = 3 + t_{1} \end{cases}$ và $Δ_{2} : \{\begin{cases} x = - 3 + t_{2} \\ y = 1 + t_{2} \\ z = 5 - \sqrt{2} t_{2} \end{cases}$ (t1, t2 là tham số) (làm tròn kết quả đến hàng đơn vị của độ).

Lời giải:

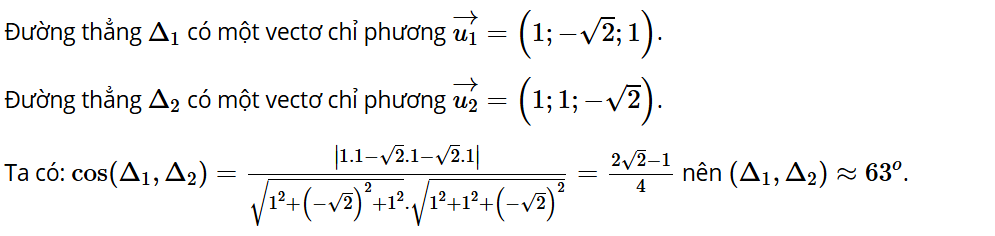
Bài tập 10: Tính góc giữa đường thẳng ∆ và mặt phẳng (P) (làm tròn kết quả đến hàng đơn vị của độ), biết $Δ : \{\begin{cases} x = - 1 + 2 t \\ y = 4 - 3 t \\ z = - 1 + 4 t \end{cases}$ (t là tham số) và (P): x + y + z + 3 = 0.

Lời giải:

Đường thẳng ∆ có vectơ chỉ phương $\vec{u} = (2; - 3; 4)$ , mặt phẳng (P) có vectơ pháp tuyến $\vec{n} = (1; 1; 1)$ .

Ta có: sin (∆, (P)) = $\frac{|2 \cdot 1 + (- 3) \cdot 1 + 4 \cdot 1|}{\sqrt{2^{2} + {(- 3)}^{2} + 4^{2}} \cdot \sqrt{1^{2} + 1^{2} + 1^{2}}} = \frac{3}{\sqrt{29} \cdot \sqrt{3}} = \frac{\sqrt{87}}{29}$ .

Suy ra (∆, (P)) ≈ 19°.

Bài tập 11: Tính góc giữa hai mặt phẳng (P1) và (P2), biết

(P1): 2x + 2y – z – 1 = 0 và (P2): x – 2y – 2z + 3 = 0.

Lời giải:

Ta có:

Vectơ pháp tuyến của là

Góc giữa hai mặt phẳng chính là góc giữa hai vectơ pháp tuyến của chúng:

Bài tập 12: Trong không gian với hệ trục toạ độ Oxyz, cho hình lập phương OBCD.O'B'C'D' có O(0; 0; 0), B(a; 0; 0), D(0; a; 0), O'(0; 0; a) với a > 0.

a) Chứng minh rằng đường chéo O'C vuông góc với mặt phẳng (OB'D').

b) Chứng minh rằng giao điểm của đường chéo O'C và mặt phẳng (OB'D') là trọng tâm của tam giác OB'D'.

c) Tính khoảng cách từ điểm B' đến mặt phẳng (C'BD).

d) Tính côsin góc giữa hai mặt phẳng (CO'D) và (C'BD).

Lời giải:

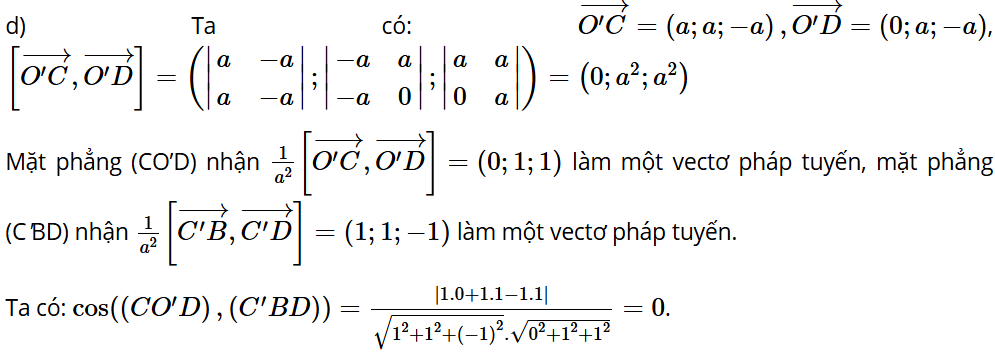
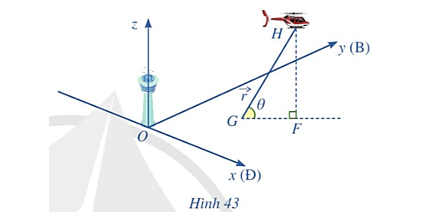
Bài tập 13: Hình 43 minh hoạ đường bay của một chiếc trực thăng H cất cánh từ một sân bay. Xét hệ trục toạ độ Oxyz có gốc toạ độ O là chân tháp điều khiển của sân bay; trục Ox là hướng đông (Ð), trục Oy là hướng bắc (B) và trục Oz là trục thẳng đứng, đơn vị trên mỗi trục là kilômét.

Bài 13 trang 89 Toán 12 Cánh diều Tập 2 | Giải Toán 12

Trực thăng cất cánh từ điểm G. Vectơ $\vec{r}$ chỉ vị trí của trực thăng tại thời điểm t phút sau khi cất cánh (t ≥ 0) có toạ độ là: $\vec{r}$ = (1 + t; 0,5 + 2t; 2t).

a) Tìm góc θ mà đường bay tạo với phương ngang.

b) Lập phương trình đường thẳng GF, trong đó F là hình chiếu của điểm H lên mặt phẳng (Oxy).

c) Trực thăng bay vào mây ở độ cao 2 km. Tìm toạ độ điểm mà máy bay trực thăng bắt đầu đi vào đám mây.

d) Giả sử một đỉnh núi nằm ở điểm A(5; 4,5; 3). Tìm giá trị của t khi HM vuông góc với đường bay GH. Tìm khoảng cách từ máy bay trực thăng đến đỉnh núi tại thời điểm đó.

Lời giải:

a) Ta có góc θ mà đường bay tạo với phương ngang chính là góc giữa đường thẳng GH và mặt phẳng (Oxy).

Tại thời điểm t = 0 thì $\vec{r_{0}} = (1; 0, 5; 0)$ . Trực thăng cất cánh từ điểm G nên G(1; 0,5; 0).

Tại thời điểm t = 1, trực thăng bay đến vị trí K thuộc đường thẳng GH với K(2; 2,5; 2).

Đường thẳng GH có vectơ chỉ phương $\vec{G K} = (1; 2; 2)$ và mặt phẳng (Oxy) có vectơ pháp tuyến $\vec{k} = (0; 0; 1)$ .

Ta có sin (GH, (Oxy)) = $\frac{|1 \cdot 0 + 2 \cdot 0 + 2 \cdot 1|}{\sqrt{1^{2} + 2^{2} + 2^{2}} \cdot \sqrt{0^{2} + 0^{2} + 1^{2}}} = \frac{2}{3}$ .

Suy ra (GH, (Oxy)) ≈ 42°. Vậy θ ≈ 42°.

b) Gọi K' là hình chiếu của điểm K lên mặt phẳng (Oxy). Khi đó K'(2; 2,5; 0).

Vì F là hình chiếu của điểm H lên mặt phẳng (Oxy) nên K' ∈ GF.

Do đó đường thẳng GF có vectơ chỉ phương là $\vec{G K^{'}} = (1; 2; 0)$ .

Phương trình tham số của đường thẳng GF là $\{\begin{cases} x = 1 + t^{'} \\ y = 0, 5 + 2 t^{'} \\ z = 0 \end{cases}$ (t' là tham số).

c) Trực thăng bay vào mây ở độ cao 2 km, tức là vị trí điểm mà trực thăng bắt đầu đi vào đám mây có cao độ z = 2, khi đó 2t = 2, suy ra t = 1.

Vậy tọa độ điểm mà trực thăng bắt đầu đi vào đám mây là (2; 2,5; 2).

d) Ta có H(1 + t; 0,5 + 2t; 2t). Khi đó, $\vec{H M} = (4 - t; 4 - 2 t; 3 - 2 t)$ .

Đường thẳng GH có vectơ chỉ phương $\vec{G K} = (1; 2; 2)$ .

HM vuông góc với đường bay GH khi $\vec{H M} ⊥ \vec{G K}$ $\Leftrightarrow \vec{H M} \cdot \vec{G K} = 0$

⇔ (4 – t) ∙ 1 + (4 – 2t) ∙ 2 + (3 – 2t) ∙ 2 = 0 ⇔ t = 2.

Vậy t = 2 thì HM vuông góc với đường bay GH.

Khi đó, khoảng cách từ đỉnh núi đến máy bay trực thăng là:

HM = $\sqrt{{(4 - 2)}^{2} + {(4 - 2 \cdot 2)}^{2} + {(3 - 2 \cdot 2)}^{2}} = \sqrt{5}$ (km).

Bài tập 14: Trong không gian với hệ toạ độ Oxyz, đài kiểm soát không lưu sân bay có toạ độ O(0; 0; 0), mỗi đơn vị trên trục ứng với 1 km. Máy bay bay trong phạm vi cách đài kiểm soát 417 km sẽ hiển thị trên màn hình ra đa. Một máy bay đang ở vị trí A(– 688; – 185; 8), chuyển động theo đường thẳng d có vectơ chỉ phương là $\vec{u} = (91; 75; 0)$ và hướng về đài kiểm soát không lưu (Hình 44).

Bài 14 trang 89 Toán 12 Cánh diều Tập 2 | Giải Toán 12

a) Xác định toạ độ của vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa.

b) Xác định toạ độ của vị trí mà máy bay bay gần đài kiểm soát không lưu nhất. Tính khoảng cách giữa máy bay và đài kiểm soát không lưu lúc đó.

c) Xác định toạ độ của vị trí mà máy bay ra khỏi màn hình ra đa.

Lời giải:

Để xác định tọa độ của vị trí sớm nhất mà máy bay xuất hiện trên màn hình radar, ta cần tìm tọa độ của điểm mà máy bay bắt đầu đi vào phạm vi 417 km từ đài kiểm soát không lưu O(0,0,0).

Phương trình đường thẳng đi qua điểm A(-688; 185; 8) và có vectơ chỉ phương :

Phương trình tham số của đường thẳng có dạng:

Máy bay sẽ xuất hiện trên màn hình radar khi khoảng cách từ máy bay tới đài kiểm soát không lưu bằng 417 km. Ta có:

Trong đó:

Giải phương trình bậc hai này để tìm t :

Chọn nghiệm = 3.62 (vì máy bay bay về phía đài kiểm soát nên sẽ gặp màn hình radar sớm hơn):

Vậy tọa độ của vị trí sớm nhất mà máy bay xuất hiện trên màn hình radar là (-359.78; 456.50; 8).

Khoảng cách từ một điểm đến một đường thẳng trong không gian được tính bằng cách chiếu vectơ từ điểm đó đến một điểm bất kỳ trên đường thẳng lên vectơ chỉ phương của đường thẳng.

Ta có: