Giải SGK Toán 12 Chân trời sáng tạo Bài 1: Phương trình mặt phẳng

Hoạt động khởi động: Trong không gian Oxyz, làm thế nào để xác định một mặt phẳng bằng phương pháp tọa độ?

Lời giải:

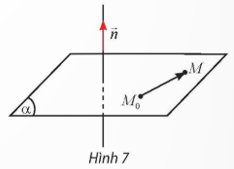
- Trong không gian Oxyz, để xác định một mặt phẳng ta cần biết được 1 điểm mà đường thẳng đó đi và một vectơ pháp tuyến của mặt phẳng đó.

1. Vectơ pháp tuyến và cặp vectơ chỉ phương của mặt phẳng

Hoạt động khám phá 1:

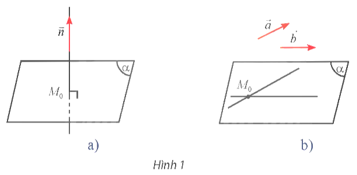
a) Cho vectơ $\overrightarrow{n}$ khác $\overrightarrow{0}$. Qua một điểm M0 cố định trong không gian, có bao nhiêu mặt phẳng (α) vuông góc với giá của vectơ $\overrightarrow{n}$?

b) Cho hai vectơ $\overrightarrow{a},\overrightarrow{b}$ không cùng phương. Qua một điểm M0 cố định trong không gian, có bao nhiêu mặt phẳng (α) song song hoặc chứa giá của hai vectơ $\overrightarrow{a},\overrightarrow{b}$?

Lời giải:

Thực hành 1: Trong không gian Oxyz, cho ba điểm A(3; 0; 0), B(0; 4; 0), C(0; 0; 5).

a) Tìm tọa độ của một cặp vectơ chỉ phương của mặt phẳng (ABC).

b) Tìm tọa độ của một vectơ pháp tuyến của mặt phẳng (OAB).

Lời giải:

a) Vì  và  không cùng phương và có giá nằm trong mặt phẳng  nên ,  là một cặp vectơ chỉ phương của 

 và 

b) Vì  nên  là một vectơ pháp tuyến của mặt phẳng  và .

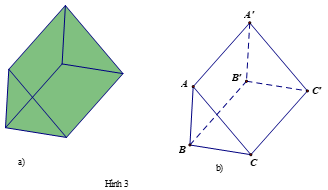
Vận dụng 1: Một lăng kính có dạng hình lăng trụ đứng có đáy là tam giác đều ở Hình 3a được vẽ lại như Hình 3b. Tìm một cặp vectơ chỉ phương và một vectơ pháp tuyến của mặt phẳng (A'B'C').

Lời giải:

+) $\overrightarrow{A^{\prime }{B}^{\prime }},\overrightarrow{A^{\prime }{C}^{\prime }}$ là cặp vectơ chỉ phương của mặt phẳng (A'B'C').

+) Vì BB' ^ (A'B'C') nên $\overrightarrow{B{B}^{\prime }}$ là một vectơ pháp tuyến của mặt phẳng (A'B'C').

2. Xác định vectơ pháp tuyến của mặt phẳng khi biết một cặp vectơ chỉ phương

Hoạt động khám phá 2: Trong không gian Oxyz, cho mặt phẳng (α) có cặp vectơ chỉ phương $\overrightarrow{a}=\left(a_1;a_2;a_3\right)$, $\overrightarrow{b}=\left(b_1;b_2;b_3\right)$. Xét vectơ $\overrightarrow{n}=\left(a_2{b}_3-a_3{b}_2;a_3{b}_1-a_1{b}_3;a_1{b}_2-a_2{b}_1\right)$.

a) Vectơ $\overrightarrow{n}$ có khác $\overrightarrow{0}$ hay không?

b) Tính $\overrightarrow{a}.\overrightarrow{n};\overrightarrow{b}.\overrightarrow{n}$.

c) Vectơ $\overrightarrow{n}$ có phải là vectơ pháp tuyến của mặt phẳng (α) không?

Lời giải:

Thực hành 2: Cho mặt phẳng (Q) đi qua ba điểm A(1; 1; 1), B(−1; 1; 5), C(10; 7; −1). Tìm cặp vectơ chỉ phương và một vectơ pháp tuyến của (Q).

Lời giải:

Ta có $\overrightarrow{AB}=\left(-2;0;4\right),\overrightarrow{AC}=\left(9;6;-2\right)$ là cặp vectơ chỉ phương của mặt phẳng (Q).

Có $\left[\overrightarrow{AB},\overrightarrow{AC}\right]=\left(\left|\begin{array}{cc}0& 4\\ 6& -2\end{array}\right|;\left|\begin{array}{cc}4& -2\\ -2& 9\end{array}\right|;\left|\begin{array}{cc}-2& 0\\ 9& 6\end{array}\right|\right)$ = $\left(-24;32;-12\right)$

Do đó mặt phẳng (Q) nhận $\overrightarrow{n}=\frac{1}{4}\left[\overrightarrow{AB},\overrightarrow{AC}\right]=\left(-6;8;-3\right)$ làm một vectơ pháp tuyến.

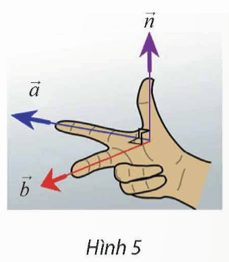
Vận dụng 2: Cho biết hai vectơ $\overrightarrow{a}=\left(2;1;1\right)$, $\overrightarrow{b}=\left(1;-2;0\right)$ có giá lần lượt song song với ngón trỏ và ngón giữa của bàn tay trong Hình 5. Tìm vectơ $\overrightarrow{n}$ có giá song song với ngón cái. (Xem như ba ngón tay nói trên tạo thành ba đường thẳng đôi một vuông góc).

Lời giải:

Vì ba ngón tay nói trên tạo thành ba đường thẳng đôi một vuông góc nên .

3. Phương trình tổng quát của mặt phẳng

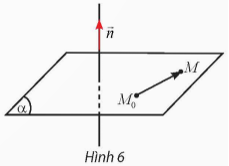
Hoạt động khám phá 3: Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M0(1; 2; 3) và nhận $\overrightarrow{n}=\left(7;5;2\right)$ làm vectơ pháp tuyến. Gọi M(x; y; z) là một điểm tùy ý trong không gian. Tính tích vô hướng $\overrightarrow{n}.\overrightarrow{M_{0}M}$ theo x, y, z.

Lời giải:

Ta có $\overrightarrow{M_{0}M}=\left(x-1;y-2;z-3\right)$.

Có $\overrightarrow{n}.\overrightarrow{M_{0}M}=7\left(x-1\right)+5\left(y-2\right)+2\left(z-3\right)$ = 7x + 5y + 2z – 23.

Thực hành 3: Cho hai mặt phẳng (α), (β) có phương trình tổng quát là (α): 2x + 2y – 3z – 4 = 0 và (β): x + 4z – 12 = 0.

a) Tìm một vectơ pháp tuyến của mỗi mặt phẳng (α), (β).

b) Tìm điểm thuộc mặt phẳng (α) trong số các điểm: M(1; 0; 1), N(1; 1; 0).

Lời giải:

a) Mặt phẳng  có một vectơ pháp tuyến là 

Mặt phẳng  có một vectơ pháp tuyến là 

b) Thay toạ độ điểm  vào phương trình của  ta được:

Vậy  không thuộc  

Thay toạ độ điểm  vào phương trình của  ta được: 

Vậy  thuộc  

Hoạt động khám phá 4: Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M0(x0; y0; z0) và nhận $\overrightarrow{n}=\left(A;B;C\right)$ làm vectơ pháp tuyến. Gọi M(x; y; z) là một điểm tùy ý trong không gian.

a) Tìm tọa độ của $\overrightarrow{M_{0}M}$.

b) Tính tích vô hướng của $\overrightarrow{n}.\overrightarrow{M_{0}M}$.

c) Lập phương trình tổng quát của mặt phẳng (α).

Lời giải:

Hoạt động khám phá 5: Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M(0; 2; 1) và có cặp vectơ chỉ phương là $\overrightarrow{a}=\left(1;3;1\right),\overrightarrow{b}=\left(2;0;1\right)$.

a) Tìm tọa độ một vectơ pháp tuyến của mặt phẳng (α).

b) Lập phương trình của mặt phẳng (α)

Lời giải:

a) Có $\left[\overrightarrow{a},\overrightarrow{b}\right]=\left(\left|\begin{array}{cc}3& 1\\ 0& 1\end{array}\right|;\left|\begin{array}{cc}1& 1\\ 1& 2\end{array}\right|;\left|\begin{array}{cc}1& 3\\ 2& 0\end{array}\right|\right)=\left(3;1;-6\right)$.

Mặt phẳng (α) nhận $\overrightarrow{n}=\left[\overrightarrow{a},\overrightarrow{b}\right]=\left(3;1;-6\right)$ làm một vectơ pháp tuyến.

b) Mặt phẳng (α) đi qua M(0; 2; 1) và nhận $\overrightarrow{n}=\left(3;1;-6\right)$ làm một vectơ pháp tuyến có phương trình là: 3x + (y – 2) – 6(z – 1) = 0 ⇔ 3x + y – 6z + 4 = 0.

Hoạt động khám phá 6: Trong không gian Oxyz, cho mặt phẳng (α) đi qua ba điểm A(0; 1; 1), B(2; 4; 3), C(5; 3; 1).

a) Tìm tọa độ một cặp vectơ chỉ phương của mặt phẳng (α).

b) Tìm tọa độ một vectơ pháp tuyến của mặt phẳng (α).

c) Lập phương trình của mặt phẳng (α).

Lời giải:

a) Mặt phẳng  đi qua ba điểm , ,  nên có cặp vectơ chỉ phương là  và , 

b) Mặt phẳng  có vecto pháp tuyến là:

c) Vì  đi qua điểm  và có vectơ pháp tuyến  nên có phương trình là:

Thực hành 4: Viết phương trình mặt phẳng (P) trong mỗi trường hợp sau:

a) (P) đi qua điểm A(2; 0; −1) và có vectơ pháp tuyến $\overrightarrow{n}=\left(5;-2;7\right)$.

b) (P) đi qua điểm B(−2; 3; 0) và có cặp vectơ chỉ phương là $\overrightarrow{u}=\left(2;2;-1\right)$, $\overrightarrow{v}=\left(3;1;0\right)$.

c) (P) đi qua ba điểm A(2; 1; 5), B(3; 2; 7), C(4; 1; 6).

d) (P) đi qua ba điểm M(7; 0; 0), N(0; −2; 0), P(0; 0; 9).

Lời giải:

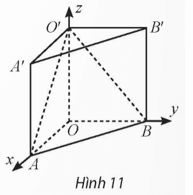
Vận dụng 3: Trong không gian Oxyz, cho hình lăng trụ OAB.O'A'B'. Biết O là gốc tọa độ, A(2; 0; 0), B(0; 3; 0), O'(0; 0; 5). Viết phương trình các mặt phẳng (O'AB) và (O'A'B').

Lời giải:

Mặt phẳng  đi qua 3 điểm , ,  nên có cặp vectơ chỉ phương là  và , suy ra  có 

Phương trình của  là:  

, 

Tương tự, mặt phẳng  có cặp vectơ chỉ phương là  và , suy ra  có  

Phương trình của  là:  

4. Điều kiện để hai mặt phẳng song song, vuông góc

Hoạt động khám phá 7: Cho hai mặt phẳng (α), (β) có phương trình là (α): x – 2y + 3z + 1 = 0 và (β): 2x – 4y + 6z + 1 = 0.

a) Nêu nhận xét về các vectơ pháp tuyến của hai mặt phẳng trên.

b) Cho điểm M(−1; 0; 0). Hãy cho biết các mặt phẳng (α), (β) có đi qua M không.

c) Giải thích tại sao (α) song song với (β).

Lời giải:

a) Ta có $\overrightarrow{n_{\alpha }}=\left(1;-2;3\right),\overrightarrow{n_{\beta }}=\left(2;-4;6\right)=2\overrightarrow{n_{\alpha }}$.

Hai vectơ pháp tuyến cùng phương với nhau.

b) Thay tọa độ điểm M vào phương trình (α) ta được: −1 + 1 = 0.

Vậy điểm M ∈ (α).

Thay tọa độ điểm M vào vào phương trình (β) ta được 2.(−1) + 1 = −1 ≠ 0.

Vậy điểm M ∉ (β).

c) Vì $\overrightarrow{n_{\beta }}=2\overrightarrow{n_{\alpha }}$ và M ∈ (α), M ∉ (β) nên (α) song song với (β).

Thực hành 5: Mặt phẳng (E): 2x – y + 8z + 1 = 0 song song với mặt phẳng nào sau đây?

a) (F): 8x – 4y + 32z + 7 = 0;

b) (H): 6x – 3y + 24z + 3 = 0;

c) (G): 10x – 5y + 41z + 1 = 0.

Lời giải:

Các mặt phẳng  có các vecto pháp tuyến lần lượt là:

, , , 

a) , . Vậy 

b) , . Vậy 

c)  suy ra  và  không cùng phương. Vậy  cắt 

Vận dụng 4: Trên bản thiết kế đồ họa 3D của một cách đồng điện mặt trời trong không gian Oxyz, một tấm pin nằm trên mặt phẳng (P): 6x + 5y + z + 2 = 0; một tấm pin khác nằm trên mặt phẳng (Q) đi qua điểm M(1; 1; 1) và song song với (P). Viết phương trình mặt phẳng (Q).

Lời giải:

Hoạt động khám phá 8: Cho hai mặt phẳng (α) và (β) có phương trình là (α): 3x + 2y + z + 1 = 0 và (β): 5x – 10y + 5z + 9 = 0.

a) Chỉ ra hai vectơ $\overrightarrow{n_1},\overrightarrow{n_2}$ lần lượt là vectơ pháp tuyến của (α) và (β).

b) Tính tích vô hướng $\overrightarrow{n_1},\overrightarrow{n_2}$ và nêu nhận xét về hai mặt phẳng (α) và (β).

Lời giải:

a) Có $\overrightarrow{n_1}=\left(3;2;1\right),\overrightarrow{n_2}=\left(5;-10;5\right)$.

b) $\overrightarrow{n_1}.\overrightarrow{n_2}=3.5+2.\left(-10\right)+1.5=0$.

Do đó (α) ⊥ (β).

Thực hành 6: Tìm các cặp mặt phẳng vuông góc trong các mặt phẳng sau:

(F): 3x + 2y + 5z + 3 = 0; (H): x – 4y + z + 23 = 0; (G): x – y + 3z + 24 = 0.

Lời giải:

Các mặt phẳng  có vecto pháp tuyến lần lượt là: , , 

 . Vậy  

 . Vậy  và  không vuông góc với nhau

 . Vậy  

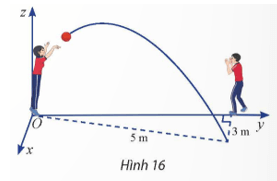
Vận dụng 5: Hai học sinh đang chuyền bóng. Bạn nữ ném bóng cho bạn nam. Quả bóng bay trên không, lệch sang phải và rơi xuống tại vị trí cách bạn nam 3 m, cách bạn nữ 5 m (Hình 16). Cho biết quỹ đạo của quả bóng nằm trong mặt phẳng (P) vuông góc với mặt đất. Hãy viết phương trình của (P) trong không gian Oxyz được mô tả như trong hình vẽ.

Lời giải:

5. Khoảng cách từ một điểm đến một mặt phẳng

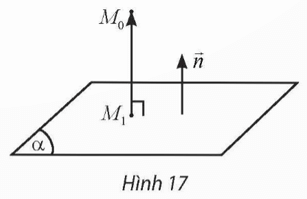
Hoạt động khám phá 9: Trong không gian Oxyz, cho mặt phẳng (α) có phương trình Ax + By + Cz + D = 0 và điểm M0(x0; y0; z0). Gọi M1(x1; y1; z1) là hình chiếu vuông góc của M0 trên (α) (Hình 17).

a) Nêu nhận xét về phương của hai vectơ $\overrightarrow{M_1{M}_0}=\left(x_0-x_1;y_0-y_1;z_0-z_1\right)$ và $\overrightarrow{n}=\left(A;B;C\right)$.

b) Tính $\overrightarrow{M_1{M}_0}.\overrightarrow{n}$ theo A, B, C, D và tọa độ của M0.

c) Giải thích tại sao ta lại có đẳng thức $\left|\overrightarrow{M_1{M}_0}\right|.\left|\overrightarrow{n}\right|=\left|\overrightarrow{M_1{M}_0}.\overrightarrow{n}\right|$

d) Từ các kết quả trên suy ra cách tính $d\left(M_0,\left(\alpha \right)\right)=\left|\overrightarrow{M_1{M}_0}\right|=\frac{\left|}{\overrightarrow{M_1{M}_0}.\overrightarrow{n}}$

Lời giải:

a) Vì M1(x1; y1; z1) là hình chiếu vuông góc của M0 trên (α) nên M1M0 ^ (α).

Do đó hai vectơ $\overrightarrow{M_1{M}_0}=\left(x_0-x_1;y_0-y_1;z_0-z_1\right)$ và $\overrightarrow{n}=\left(A;B;C\right)$ cùng phương với nhau.

b) $\overrightarrow{M_1{M}_0}.\overrightarrow{n}=A\left(x_0-x_1\right)+B\left(y_0-y_1\right)+C\left(z_0-z_1\right)$

= Ax0 + By0 + Cz0 – Ax1 – By1 – Cz1.

Vì M1(x1; y1; z1) Î (α) nên ta có Ax1 + By1 + Cz1 + D = 0 ⇔ D = – Ax1 – By1 – Cz1.

Do đó $\overrightarrow{M_1{M}_0}.\overrightarrow{n}$ = Ax0 + By0 + Cz0 + D.

c) Ta có $\overrightarrow{M_1{M}_0}.\overrightarrow{n}=\left|\overrightarrow{M_1{M}_0}\right|.\left|\overrightarrow{n}\right|.\cos \left(\overrightarrow{M_1{M}_0},\overrightarrow{n}\right)$.

Mà do hai vectơ $\overrightarrow{M_1{M}_0}$ và $\overrightarrow{n}$ cùng phương với nhau nên $\left(\overrightarrow{M_1{M}_0},\overrightarrow{n}\right)=0°$ hoặc $\left(\overrightarrow{M_1{M}_0},\overrightarrow{n}\right)=180°$.

+) Nếu $\left(\overrightarrow{M_1{M}_0},\overrightarrow{n}\right)=0°$ thì $\overrightarrow{M_1{M}_0}.\overrightarrow{n}=\left|\overrightarrow{M_1{M}_0}\right|.\left|\overrightarrow{n}\right|$.

+) Nếu $\left(\overrightarrow{M_1{M}_0},\overrightarrow{n}\right)=180°$ thì $\overrightarrow{M_1{M}_0}.\overrightarrow{n}=-\left|\overrightarrow{M_1{M}_0}\right|.\left|\overrightarrow{n}\right|$

Do đó $\left|\overrightarrow{M_1{M}_0}\right|.\left|\overrightarrow{n}\right|=\left|\overrightarrow{M_1{M}_0}.\overrightarrow{n}\right|$.

d) Vì $\left|\overrightarrow{M_1{M}_0}\right|.\left|\overrightarrow{n}\right|=\left|\overrightarrow{M_1{M}_0}.\overrightarrow{n}\right|$ nên

$d\left(M_0,\left(\alpha \right)\right)=\left|\overrightarrow{M_1{M}_0}\right|=\frac{\left|}{\overrightarrow{M_1{M}_0}.\overrightarrow{n}}=\frac{\left|}{A{x}_0+B{y}_0+C{z}_0+D}$

Thực hành 7:

a) Tính chiều cao của hình chóp O.MNP với tọa độ các đỉnh là O(0; 0; 0), M(2; 1; 2), N(3; 3; 3), P(4; 5; 6).

b) Tính khoảng cách giữa hai mặt phẳng song song (R): 8x + 6y + 70 = 0 và (S): 16x + 12y – 2 = 0.

Lời giải:

a) Mặt phẳng  đi qua 3 điểm , ,  nên có cặp vectơ chỉ phương là  và 

=>  có  

Phương trình của  là: 

Chiều cao  của hình chóp  chính là khoảng cách từ đỉnh  đến .

b) Ta lấy điểm  thuộc 

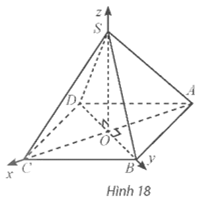
Vận dụng 6: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng $a\sqrt{2}$, chiều cao bằng 2a và O là tâm của đáy. Bằng cách thiết lập hệ trục tọa độ Oxyz như Hình 18, tính khoảng cách từ điểm C đến mặt phẳng (SAB).

Lời giải:

Bài tập

Bài tập 1: Viết phương trình của mặt phẳng:

a) Đi qua điểm A(2; 0; 0) và nhận $\overrightarrow{n}=\left(2;1;-1\right)$ làm vectơ pháp tuyến;

b) Đi qua điểm B(1; 2; 3) và song song với giá của mỗi vectơ $\overrightarrow{u}=\left(1;2;3\right)$ và $\overrightarrow{v}=\left(-2;0;1\right)$;

c) Đi qua ba điểm A(1; 0; 0), B(0; 2; 0) và C(0; 0; 4).

Lời giải:

a) Vì  đi qua điểm  và có vectơ pháp tuyến  nên có phương trình là:

b)  có cặp vectơ chỉ phương là , , suy ra  có  

Phương trình của  là:  

c)  đi qua ba điểm  nên có cặp vectơ chỉ phương là  và , suy ra  có 

Phương trình của  là:  

Bài tập 2:

a) Lập phương trình của các mặt phẳng tọa độ (Oxy), (Oyz), (Oxz).

b) Lập phương trình của các mặt phẳng đi qua điểm A(−1; 9; 8) và lần lượt song song với các mặt phẳng tọa độ trên.

Lời giải:

a) Mặt phẳng (Oxy) nhận $\overrightarrow{k}=\left(0;0;1\right)$ làm vectơ pháp tuyến có phương trình là z = 0.

Mặt phẳng (Oyz) nhận $\overrightarrow{i}=\left(1;0;0\right)$  làm vectơ pháp tuyến có phương trình là x = 0.

Mặt phẳng (Oxz) nhận $\overrightarrow{j}=\left(0;1;0\right)$ làm vectơ pháp tuyến có phương trình là y = 0.

b) Mặt phẳng đi qua điểm A(−1; 9; 8) và song song với mặt phẳng (Oxy) nhận $\overrightarrow{k}=\left(0;0;1\right)$ làm vectơ pháp tuyến có phương trình là z – 8 = 0.

Mặt phẳng đi qua điểm A(−1; 9; 8) và song song với mặt phẳng (Oyz) nhận $\overrightarrow{i}=\left(1;0;0\right)$ làm vectơ pháp tuyến có phương trình là x + 1 = 0.

Mặt phẳng đi qua điểm A(−1; 9; 8) và song song với mặt phẳng (Oxz) nhận $\overrightarrow{j}=\left(0;1;0\right)$ làm vectơ pháp tuyến có phương trình là y – 9 = 0.

Bài tập 3: Cho tứ diện ABCD có các đỉnh A(4; 0; 2), B(0; 5; 1), C(4; −1; 3), D(3; −1; 5).

a) Hãy viết phương trình của các mặt phẳng (ABC) và (ABD).

b) Hãy viết phương trình mặt phẳng (P) đi qua cạnh BC và song song với cạnh AD.

Lời giải:

Bài tập 4: Viết phương trình mặt phẳng (Q) đi qua C(1; −5; 0) và song song với mặt phẳng (P): 3x – 5y + 4z – 2024 = 0.

Lời giải:

Có $\overrightarrow{n_P}=\left(3;-5;4\right)$.

Vì (Q) // (P) nên mặt phẳng (Q) nhận $\overrightarrow{n_P}=\left(3;-5;4\right)$ làm một vectơ pháp tuyến.

Mặt phẳng (Q) đi qua điểm C(1; −5; 0) và có một vectơ pháp tuyến $\overrightarrow{n_P}=\left(3;-5;4\right)$ có phương trình là 3(x – 1) – 5(y + 5) + 4z = 0 ⇔ 3x – 5y + 4z – 28 = 0.

Bài tập 5: Viết phương trình mặt phẳng (α) đi qua hai điểm A(1; 0; 1), B(5; 2; 3) và vuông góc với mặt phẳng (β): 2x – y + z – 7 = 0.

Lời giải:

Mặt phẳng  có vecto pháp tuyến là 

Do ( nên  song song với  

Mặt phẳng  có cặp vectơ chỉ phương là  và , suy ra  có

Phương trình của  là: 

Bài tập 6: Viết phương trình mặt phẳng (R) đi qua điểm A(1; 2; −1) và vuông góc với hai mặt phẳng (P): 4x – 2y + 6z – 11 = 0, (Q): 2x + 2y + 2z – 7 = 0.

Lời giải:

Bài tập 7: Tính khoảng cách từ gốc tọa độ và từ điểm M(1; −2; 13) đến mặt phẳng (P): 2x – 2y – z + 3 = 0.

Lời giải:

+) $d\left(O,\left(P\right)\right)=\frac{\left|}{3}=1$

+) $d\left(M,\left(P\right)\right)=\frac{\left|}{2.1-2.\left(-2\right)-13+3}=\frac{4}{3}$

Bài tập 8: Tính khoảng cách giữa hai mặt phẳng song song (P): x – 2 = 0 và (Q): x – 8 = 0.

Lời giải:

Ta lấy điểm  thuộc . Do hai mặt phẳng  và  song song nên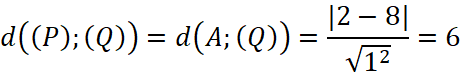 

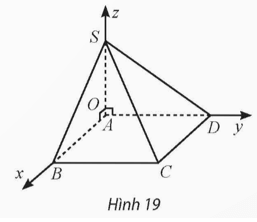
Bài tập 9: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a, AD = 5a, SA = 3a và SA ⊥ (ABCD). Bằng cách thiết lập hệ trục tọa độ Oxyz như Hình 19, tính khoảng cách từ điểm A đến mặt phẳng (SBC).

Lời giải:

Bài tập 10: Một công trường xây dựng nhà cao tầng đã thiết lập hệ tọa độ Oxyz. Hãy kiểm tra tính song song hoặc vuông góc giữa các mặt kính (P), (Q), (R) (Hình 20) của một tòa nhà, biết: (P): 3x + y – z + 2 = 0; (Q): 6x + 2y – 2z + 11 = 0; (R): x – 3y + 1 = 0.

Lời giải:

Có $\overrightarrow{n_P}=\left(3;1;-1\right),\overrightarrow{n_Q}=\left(6;2;-2\right),\overrightarrow{n_R}=\left(1;-3;0\right)$.

Có $\overrightarrow{n_Q}=2\left(3;1;-1\right)=2\overrightarrow{n_P}$ và 11 ≠ 2.2. Do đó (P) // (Q).

Có $\overrightarrow{n_P}.\overrightarrow{n_R}=3.1+1.\left(-3\right)+\left(-1\right).0=0$. Do đó (P) ⊥ (R).

Có $\overrightarrow{n_Q}.\overrightarrow{n_R}=6.1+2.\left(-3\right)+\left(-2\right).0=0$. Do đó (Q) ⊥ (R).