Giải SGK Toán 11 Cánh Diều Bài tập cuối chương VI

Bài tập 1: Điều kiện xác định của x–3 là:

A. x∈ ℝ.    

B. x ≥ 0.     

C. x ≠ 0.     

D. x > 0.

Đáp án: C

Bài tập 2: Điều kiện xác định của $x^{\frac{3}{5}}$  là:

A. x∈ ℝ.    

B. x ≥ 0.     

C. x ≠ 0.     

D. x > 0.

Đáp án: A

Ta có: $x^{\frac{3}{5}}=\sqrt[5]{5x^3}$

Khi đó hàm số $x^{\frac{3}{5}}=\sqrt[5]{5x^3}$  xác định với mọi x∈ ℝ.  

Bài tập 3: Tập xác định của hàm số y = log0,5(2x – x2) là:

A. (–∞; 0) ∪ (2; +∞).

B. ℝ \{0; 2}.

C. [0; 2].     

D. (0; 2).

Đáp án: D

y=log0,5(2x−x2)

=>2x−x2>0 => 0<x<2 

Bài tập 4: Hàm số nào sau đây đồng biến trên tập xác định của nó?

A. y = (0,5)x.             

B. $y={\left(\frac{2}{3}\right)}^x.$

C. $y={\left(\sqrt{2}\right)}^x.$

D. $y={\left(\frac{e}{\pi }\right)}^x.$

Đáp án: C

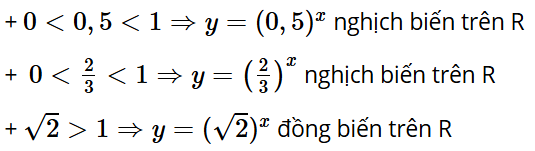
Bài tập 5: Hàm số nào sau đây nghịch biến trên tập xác định của nó?

A. y = log3x.

B. $y={\log }_{\sqrt{3}}x$.       

C. $y={\log }_{\frac{1}{e}}x$.        

D. y = logπx.

Đáp án: C

Hàm số y = logax nghịch biến trên tập xác định của nó khi 0 < a < 1.

Mà $3>\mathrm{1,}\sqrt{3}>\mathrm{1,}\pi >\mathrm{1,0}<\frac{1}{e}<1$

Suy ra hàm số $y={\log }_{\frac{1}{e}}x$nghịch biến trên tập xác định của nó.

Bài tập 6: Nếu 3x = 5 thì 32x bằng:

A. 15.

B. 125.       

C. 10.

D. 25.

Đáp án: D

Vì 3x=5 => x=log35

Có 32x=32log35 => x=25

Bài tập 7: Cho $A=4^{{\log }_{2}3}.$  Khi đó giá trị của A bằng:

A. 9. 

B. 6. 

C. $\sqrt{3}.$

D. 81.

Đáp án: A

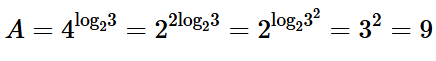
Bài tập 8: Nếu logab = 3 thì logab2 bằng:

A. 9.                              

B. 5.                    

C. 6.                    

D. 8.

Đáp án: C

Ta có: logab2 = 2logab = 2 . 3 = 6.

Bài tập 9: Nghiệm của phương trình 32x – 5 = 27 là:

A. 1. 

B. 4. 

C. 6. 

D. 7.

Đáp án: B

32x−5=27

<=> 2x−5=3

<=> x=4

Bài tập 10: Nghiệm của phương trình log0,5(2 – x) = –1 là:

A. 0. 

B. 2,5.        

C. 1,5.        

D. 2.

Đáp án: A

Ta có log0,5(2 – x) = –1 ⇔ 2 – x = 0,5–1 ⇔ 2 – x = 2 ⇔ x = 0.

Bài tập 11: Tập nghiệm của bất phương trình (0,2)x > 1 là:

A. (–∞; 0,2).

B. (0,2; +∞).

C. (0; +∞).  

D. (–∞; 0).

Đáp án: D

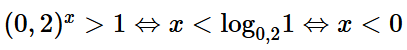
Bài tập 12: Tập nghiệm của bất phương trình ${\log }_{\frac{1}{4}}x>-2$  là:

A. (–∞; 16).

B. (16; +∞).

C. (0; 16).   

D. (–∞; 0).

Đáp án: C

Ta có ${\log }_{\frac{1}{4}}x>-2\iff 0<x<{\left(\frac{1}{4}\right)}^{-2}\iff 0<x<16$

Vậy bất phương trình đã cho có tập nghiệm là (0; 16).

Bài tập 13: Cho ba số thực dương a, b, c khác 1 và đồ thị ba hàm số mũ y = ax, y = bx, y = cx được cho bởi Hình 14.

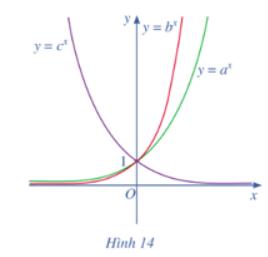
Kết luận nào sau đây là đúng đối với ba số a, b, c?

A. c < a < b.

B. c < b < a.

C. a < b < c.

D. b < c < a.

Đáp án: A

Từ các đồ thị hàm số trên Hình 14 ta thấy:

⦁ Hàm số y = cx nghịch biến trên ℝ nên 0 < c < 1;

⦁ Hai hàm số y = ax và y = bx đồng biến trên ℝ nên a > 1 và b > 1.

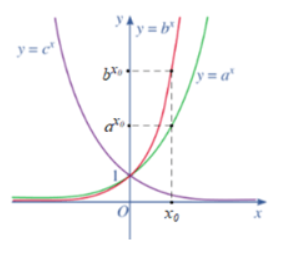
Thay cùng giá trị của x = x0 (với x0 > 0) vào hai hàm số y = ax và y = bx ta thấy  nên a < b

Suy ra c < a < b.

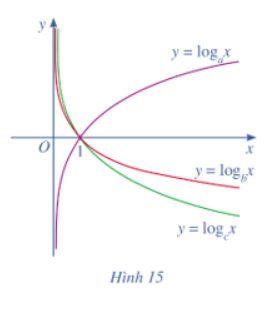
Bài tập 14: Cho ba thực dương a, b, c khác 1 và đồ thị ba hàm số lôgarit y = logax, y = logbx, y = logcx được cho bởi Hình 15. Kết luận nào sau đây là đúng với ba số a, b, c?

A. c < a < b.

B. c < b < a.

C. a < b < c.

D. b < c < a.

Đáp án: D

Từ các đồ thị hàm số trên Hình 15 ta thấy:

⦁ Hàm số y = logax đồng biến trên (0; +∞) nên a > 1;

⦁ Hai hàm số y = logbx và y = logcx nghịch biến trên (0; +∞) nên 0 < b < 1; 0 < c < 1.

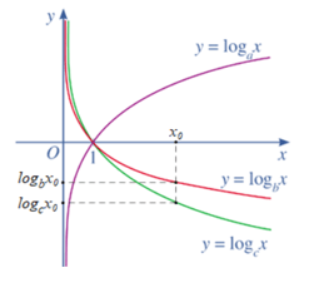
Thay cùng giá trị của x = x0 (với x0 ∈ (0; +∞)) vào hai hàm số ta thấy logbx0 > logcx0

Mà 0 < b < 1; 0 < c < 1 nên b < c.

Suy ra b < c < a.

Bài tập 15: Viết các biểu thức sau về lũy thừa cơ số a:

a) $A=\sqrt[3]{35\sqrt{\frac{1}{5}}}$với a = 5.                        b) $B=\frac{4\sqrt[5]{52}}{\sqrt[3]{34}}$ với $a=\sqrt{2}.$

Lời giải:

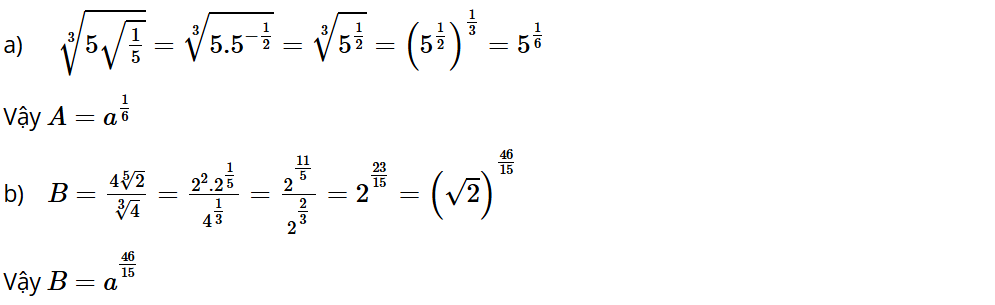
Bài tập 16: Cho x, y là các số thực dương. Rút gọn biểu thức sau:

 $A=\frac{x^{\frac{5}{4}}\cdot y+x\cdot y^{\frac{5}{4}}}{\sqrt[4]{4x}+\sqrt[4]{4y}};$                              $B={\left(\sqrt[7]{7\frac{x}{y}\sqrt[5]{5\frac{y}{x}}}\right)}^{\frac{35}{4}}.$

Lời giải:

a) A=x54.y+x.y54x√4.y√4

A=x14.x.y+x.y.y14x14+y14

A=xy(x14+y14)x14+y14=xy

b) B=(xyyx−−√5−−−−−√7)354

B=(xy⋅(xy)−15−−−−−−−−−√7)354

B=((xy)45−−−−−√7)354

B=((xy)435)354=xy

Bài tập 17: Tìm tập xác định của mỗi hàm số sau:

a) $y=\frac{5}{2^x-3};$                                         b) $y=\sqrt{25-5^x};$

c) $y=\frac{x}{1-\ln x};$                                        d) $y=\sqrt{1-{\log }_{3}x}.$

Lời giải:

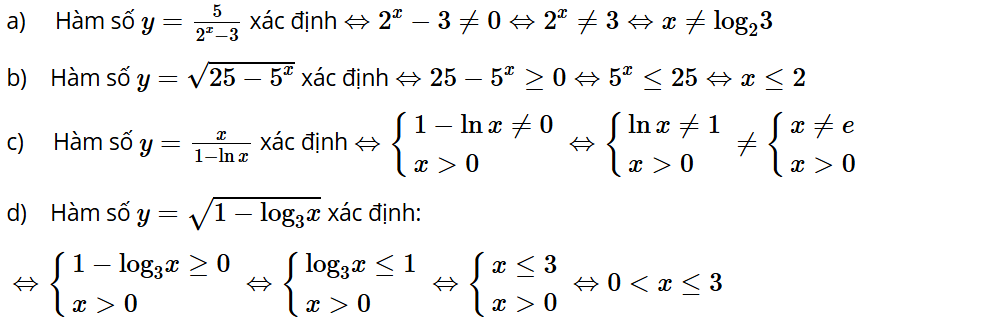
Bài tập 18: Cho a > 0, a ≠ 1 và $a^{\frac{3}{5}}=b.$

a) Viết $a^6;a^{3}b;\frac{a^9}{b^9}$  theo lũy thừa cơ số b.

b) Tính: ${\log }_{a}b;{\log }_a\left(a^2{b}^5\right);{\log }_{\sqrt[5]{5a}}\left(\frac{a}{b}\right).$

Lời giải:

a) Ta có:

⦁ ${\text{a}}^6={\left(a^{\frac{3}{5}}\right)}^{10}=b^{10};$

⦁ ${\text{a}}^{3}b={\left(a^{\frac{3}{5}}\right)}^5\cdot b=b^5\cdot b=b^6;$

⦁ $\frac{a^9}{b^9}=\frac{{\left(a^{\frac{3}{5}}\right)}^{15}}{b^9}=\frac{b^{15}}{b^9}=b^6.$

b) Ta có:

⦁ $b=a^{\frac{3}{5}}\Rightarrow {\log }_{a}b={\log }_a{a}^{\frac{3}{5}}=\frac{3}{5};$

⦁ ${\log }_a\left(a^2{b}^5\right)={\log }_a{a}^2+{\log }_a{b}^5=2{\log }_{a}a+5{\log }_{a}b=2+5\cdot \frac{3}{5}=2+3=5;$

⦁ ${\log }_{\sqrt[5]{5a}}\left(\frac{a}{b}\right)={\log }_{\sqrt[5]{5a}}a-{\log }_{\sqrt[5]{5a}}b=5{\log }_{a}a-5{\log }_{a}b=5-5\cdot \frac{3}{5}=5-3=2.$

Bài tập 19: Giải mỗi phương trình sau:

a) $3^{x^2-4x+5}=9;$                                     b) 0,52x–4 = 4;

c) log3(2x – 1) = 3;                               d) logx + log(x – 3) = 1.

Lời giải:

a) 3x2−4x+5=9

<=>x2−4x+5=2

<=>x2−4x+3=0

<=>x=3 hoặc x=1

b) 0,52x−4=4

<=>2x−4=log0,54

<=>2x−4=−2

<=>2x=2

<=>x=1

c) log3(2x−1)=3

<=>log3(2x−1)=log327

<=>2x−1=27

<=>x=14

d) logx+log(x−3)=1

ĐKXĐ: x>3

<=>log(x2−3x)=log10

<=>x2−3x=10

<=>x2−3x−10=0

<=>x=5 hoặc x=−2 (không thỏa mãn đkxđ)

=>x=5

Bài tập 20: Giải mỗi bất phương trình sau:

a)5x < 0,125;                                        b) ${\left(\frac{1}{3}\right)}^{2x+1}\ge 3;$

c) log0,3x > 0;                                        d) ln(x + 4) > ln(2x – 3).

Lời giải:

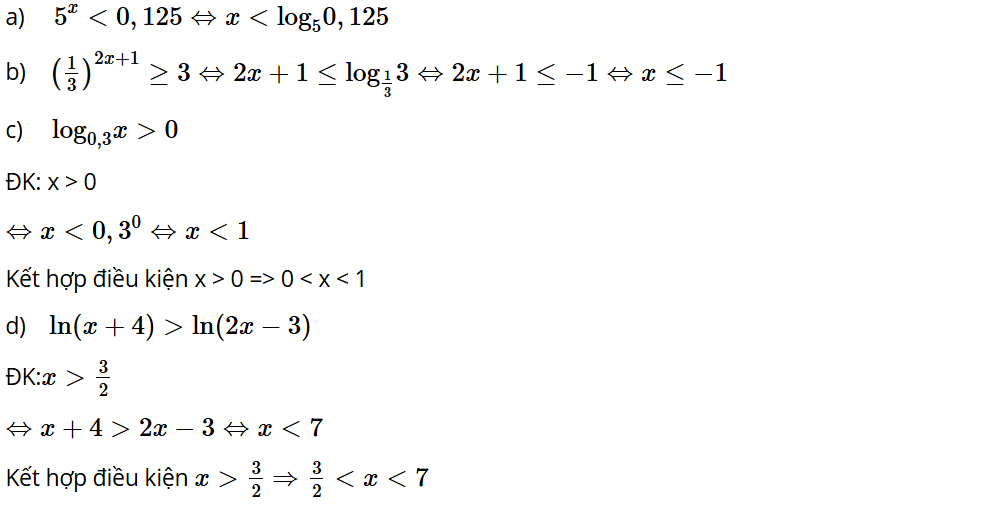
Bài tập 21: Trong một trận động đất, năng lượng giải tỏa E (đơn vị: Jun, kí hiệu J) tại tâm địa chấn ở M độ Richter được xác định xấp xỉ bởi công thức: logE ≈ 11,4 + 1,5M.

(Nguồn: Giải tích 12 Nâng cao, NXBGD Việt Nam, 2021).

a) Tính xấp xỉ năng lượng giải tỏa tại tâm địa chấn ở 5 độ Richter.

b) Năng lượng giải tỏa tại tâm địa chấn ở 8 độ Richter gấp khoảng bao nhiêu lần năng lượng giải tỏa tại tâm địa chấn ở 5 độ Richter?

Lời giải:

a) Thay M = 5 vào công thứclogE ≈ 11,4 + 1,5M, ta cónăng lượng giải tỏa tại tâm địa chấn ở 5 độ Richter là:

logE ≈ 11,4 + 1,5 . 5 =18,9

Suy ra E ≈ 1018,9 (J)

Vậynăng lượng giải toả tại tâm địa chấn ở 5 độ Richter là E ≈ 1018,9 J.

b) Thay M = 8 vào công thứclogE ≈ 11,4 + 1,5M, ta cónăng lượng giải tỏa tại tâm địa chấn ở 8 độ Richter là:

logE ≈ 11,4 + 1,5 . 8 =23,4

Suy ra E ≈ 1023,4 (J)

Do đó năng lượng giải tỏa tại tâm địa chấn ở 8 độ Richter gấp khoảng $\frac{{10}^{\mathrm{23,4}}}{{10}^{\mathrm{18,9}}}\approx 31623$ lần năng lượng giải tỏa tại tâm địa chấn ở 5 độ Richter.

Bài tập 22: Trong cây cối có chất phóng xạ $C146.$  Khảo sát một mẫu gỗ cổ, các nhà khoa học đo được độ phóng xạ của nó bằng 86% độ phóng xạ của mẫu gỗ tươi cùng loại. Xác định độ tuổi của mẫu gỗ cổ đó. Biết chu kì bán rã của $C146$  là T = 5 739 năm, độ phóng xạ của chất phóng xạ tại thời điểm t được cho bởi công thức H = H0e–λt với H0 là độ phóng xạ ban đầu (tại thời điểm t = 0); $\lambda =\frac{\ln 2}{T}$  là hằng số phóng xạ (Nguồn: Vật lí 12, NXBGD Việt Nam, 2021).

Lời giải:

Từ đó, ta có thể tính được hằng số phóng xạ:

λ=ln2T=ln25,730≈0.12

Giờ ta cần tìm thời gian t mà đã trôi qua từ thời điểm mẫu gỗ cổ được sinh ra đến thời điểm hiện tại. Để tìm thời gian này, ta sử dụng tỷ lệ phóng xạ giữa mẫu gỗ cổ và mẫu gỗ tươi cùng loại:

HH0=0.86=e−λt

t=ln0.86−λ≈3,078 năm

Vậy độ tuổi của mẫu gỗ cổ đó là khoảng 3,078 năm.