Giải SGK Toán 11 Cánh Diều Bài tập cuối chương VII

Bài tập 1: Cho u = u(x), v = v(x) là hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Phát biểu nào sau đây là đúng?

A. (uv)' = u'v'.      

B. (uv)' = uv'.

C. (uv)' = u'v.        

D. (uv)' = u'v + uv'.

Đáp án: D

Ta có: (uv)' = u'v + uv'.

Bài tập 2: Cho u = u(x), v = v(x) là hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Phát biểu nào sau đây là đúng?

A. ${\left(\frac{u}{v}\right)}^{\prime }=\frac{u\text{'}}{v^{\prime }}$ với v = v(x) ≠ 0, v' = v'(x) ≠ 0.

B. ${\left(\frac{u}{v}\right)}^{\prime }=\frac{u^{\prime }v-u{v}^{\prime }}{v}$ với v = v(x) ≠ 0.

C. ${\left(\frac{u}{v}\right)}^{\prime }=\frac{u^{\prime }v-u{v}^{\prime }}{v^2}$với v = v(x) ≠ 0.

D. ${\left(\frac{u}{v}\right)}^{\prime }=\frac{u^{\prime }v-u{v}^{\prime }}{v^{\prime }}$với v = v(x) ≠ 0, v' = v' (x) ≠ 0.

Đáp án: C

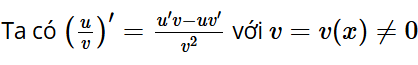
Bài tập 3: Tìm đạo hàm của mỗi hàm số sau:

a) y = (x2 + 2x)(x3 – 3x);       b) $y=\frac{1}{-2x+5};$   c) $y=\sqrt{4x+5};$

d) y = sinxcosx;                     e) y = xex;                      g) y = ln2x.

Lời giải:

a) y=(x2+2x)(x3−3x)

y′=(2x+2)(x3−3x)+(x2+2x)(3x2−3)

y′=2x4−6x2+2x3−6x+3x4−3x2+6x3−6x

y′=5x4+8x3−9x2−12x

b) y=1−2x+5

y′=2(−2x+5)2

c) y=4x+5−−−−−√

y′=424x+5√

d) y=sinxcosx

y′=cos2x−sin2x

e) y=xex

y′=ex+xex

g) y=ln2x

y′=2xlnx

Bài tập 4: Tìm đạo hàm cấp hai của mỗi hàm số sau:

a) y = 2x4 – 3x3 + 5x2;           b) $y=\frac{2}{3-x};$              c) y = sin2xcosx;

d) y = e–2x+3;                           e) y = ln(x + 1);              g) y = ln(ex + 1).

Lời giải:

a) Xét hàm số y = 2x4 – 3x3 + 5x2, ta có:

y' = 8x3 – 9x2 + 10x;

y'' = 24x2 – 18x + 10.

b) Xét hàm số $y=\frac{2}{3-x},$ ta có:

$y^{\prime }={\left(\frac{2}{3-x}\right)}^{\prime }=-\frac{2\cdot {\left(3-x\right)}^{\prime }}{{\left(3-x\right)}^2}=-\frac{2\cdot \left(-1\right)}{{\left(3-x\right)}^2}=\frac{2}{{\left(3-x\right)}^2};$

$y^{\prime \prime }={\left[\frac{2}{{\left(3-x\right)}^2}\right]}^{\prime }=-\frac{2\cdot {\left[{\left(3-x\right)}^2\right]}^{\prime }}{{\left(3-x\right)}^4}=-\frac{2\cdot 2\cdot \left(3-x\right)\cdot {\left(3-x\right)}^{\prime }}{{\left(3-x\right)}^4}=\frac{-4\cdot \left(-1\right)}{{\left(3-x\right)}^3}=\frac{4}{{\left(3-x\right)}^3}.$

c) Xét hàm số y = sin2xcosx, ta có:

y' = (sin2xcosx)' = (sin2x)'.cosx + sin2x.(cosx)'

    = 2cos2x.cosx – sin2x.sinx

$=2\cdot \frac{1}{2}\left(\cos x+\cos 3x\right)-\frac{1}{2}\left(\cos x-\cos 3x\right)$

$=\cos x+\cos 3x-\frac{1}{2}\cos x+\frac{1}{2}\cos 3x$

$=\frac{1}{2}\cos x+\frac{3}{2}\cos 3x.$

${y^{\prime }}^{\prime }={\left(\frac{1}{2}\cos x+\frac{3}{2}\cos 3x\right)}^{\prime }=\frac{1}{2}\left(-\sin x\right)+\frac{3}{2}\cdot 3\cdot \left(-\sin 3x\right)=-\frac{1}{2}\sin x-\frac{9}{2}\sin 3x.$

d) Xét hàm số y = e–2x + 3, ta có:

y' = (e–2x + 3)' = (–2x + 3)' . e–2x + 3 = –2e–2x+3;

y'' = (–2e–2x+3)' = –2.(–2x + 3)'.e–2x+3 = 4e–2x+3.

e) Xét hàm số y = ln(x + 1), ta có:

$y^{\prime }={\left[ln\left(x+1\right)\right]}^{\prime }=\frac{{\left(x+1\right)}^{\prime }}{x+1}=\frac{1}{x+1};$

${y^{\prime }}^{\prime }={\left(\frac{1}{x+1}\right)}^{\prime }=-\frac{{\left(x+1\right)}^{\prime }}{{\left(x+1\right)}^2}=-\frac{1}{{\left(x+1\right)}^2}.$

g) Xét hàm số y = ln(ex + 1), ta có:

$y^{\prime }={\left[ln\left(e^x+1\right)\right]}^{\prime }=\frac{{\left(e^x+1\right)}^{\prime }}{e^x+1}=\frac{e^x}{e^x+1};$

${y^{\prime }}^{\prime }={\left(\frac{e^x}{e^x+1}\right)}^{\prime }=\frac{{\left(e^x\right)}^{\prime }\cdot \left(e^x+1\right)-e^x\cdot {\left(e^x+1\right)}^{\prime }}{{\left(e^x+1\right)}^2}$

$=\frac{e^x\cdot \left(e^x+1\right)-e^x\cdot e^x}{{\left(e^x+1\right)}^2}=\frac{e^{2x}+e^x-e^{2x}}{{\left(e^x+1\right)}^2}=\frac{e^x}{{\left(e^x+1\right)}^2}.$

Bài tập 5: Vận tốc của một chất điểm chuyển động được biểu thị bởi công thức v(t) = 2t + t2, trong đó t > 0, t tính bằng giây và v(t) tính bằng m/s. Tìm gia tốc tức thời của chất điểm:

a) Tại thời điểm t = 3 (s);

b) Tại thời điểm mà vận tốc của chất điểm bằng 8 m/s.

Lời giải:

Bài tập 6: Một con lắc lò xo dao động điều hòa theo phương ngang trên mặt phẳng không ma sát, có phương trình chuyển động $x=4\cos \left(\pi t-\frac{2\pi }{3}\right)+\mathrm{3,}$ trong đó t tính bằng giây và x tính bằng centimet.

a) Tìm vận tốc tức thời và gia tốc tức thời của con lắc tại thời điểm t (s).

b) Tìm thời điểm mà vận tốc tức thời của con lắc bằng 0.

Lời giải:

a) Vận tốc tức thời của con lắc:

v(t)=−4πsin(πt−2π3)

Gia tốc tức thời của con lắc

a(t)=−4π2cos(πt−2π3)

b) Tại vận tốc tức thời của con lắc bằng 0, ta có

−4πsin(πt−2π3)=0

<=>sin(πt−2π3)=0

<=> πt−2π3=0

<=> t=23

Với t=23=>a(t)=−4π2cos(π23−2π3)=−4π2