Giải SGK Toán 12 Chân trời sáng tạo Bài 2: Tọa độ của vectơ trong không gian

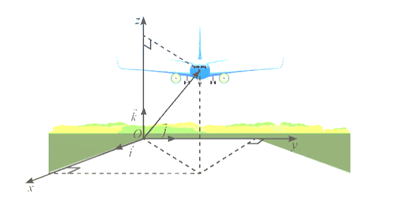
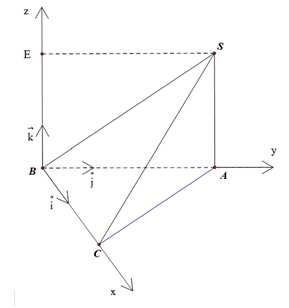
Hoạt động khởi động: Trong kiểm soát không lưu, người ta dùng bộ ba số để xác định vị trí của máy bay. Người ta đã làm điều đó như thế nào?

Trả lời:

- Xây dựng hệ tọa độ trong không gian tương tự như trong mặt phẳng, sử dụng bộ ba số để xác định hoành độ, tung độ và cao độ.

1. Hệ tọa độ trong không gian

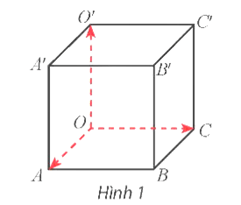
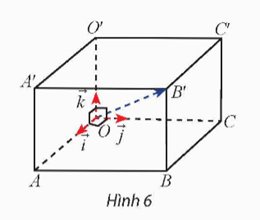
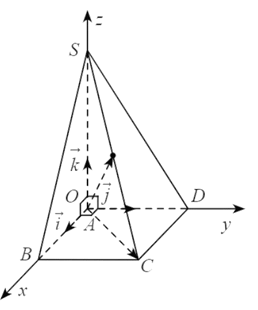
Khám phá 1: Cho hình lập phương OABC.O'A'B'C' có cạnh bằng 1. Đặt $\overrightarrow{i}=\overrightarrow{OA},\overrightarrow{j}=\overrightarrow{OC},\overrightarrow{k}=\overrightarrow{O{O}^{\prime }}$ .

a) Nêu nhận xét về phương và độ dài của ba vectơ $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$ .

b) Nêu nhận xét về ba trục tọa độ $\left(O;\overrightarrow{i}\right),\left(O;\overrightarrow{j}\right),\left(O;\overrightarrow{k}\right)$ .

Trả lời:

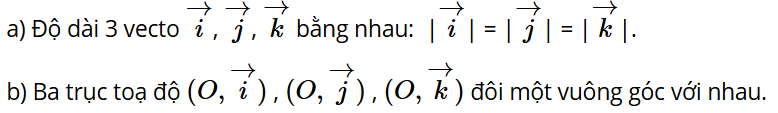
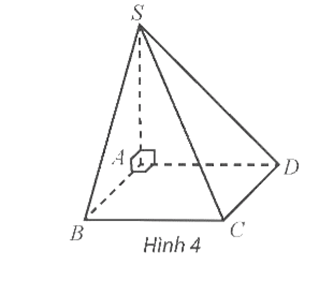
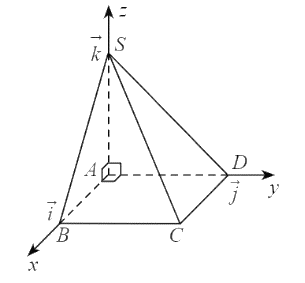
Thực hành 1: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 1, SA vuông góc với mặt phẳng đáy và có độ dài bằng 1 (Hình 4). Vẽ hệ trục tọa độ Oxyz có gốc O trùng với điểm A, các điểm B, D, S lần lượt nằm trên các tia Ox, Oy, Oz và chỉ ra các vectơ đơn vị trên các trục tọa độ.

Trả lời:

- Trục Ox có vectơ đơn vị là $\overrightarrow{AB}$ .

- Trục Oy có vectơ đơn vị là $\overrightarrow{AD}$ .

- Trục Oz có vectơ đơn vị là ${AS}^{}$ .

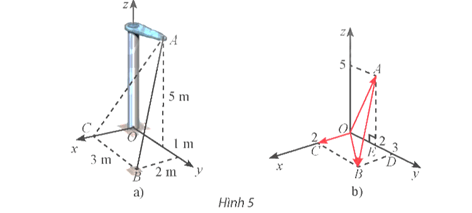
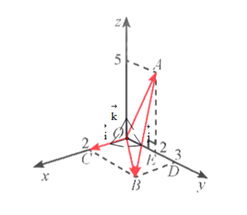
Vận dụng 1: Một thiết kế cơ khí trong Hình 5a được biểu diễn trong không gian Oxyz như Hình 5b.

a) Hãy vẽ ba vectơ đơn vị $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$ lần lượt trên ba trục tọa độ Ox, Oy, Oz (mỗi vectơ đơn vị có độ dài bằng 1 m).

b) Biểu diễn các vectơ $\overrightarrow{OC},\overrightarrow{OB},\overrightarrow{OA},\overrightarrow{AB}$ theo $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$ .

Trả lời:

a)

b) $\overrightarrow{OC}=2\overrightarrow{i}$; $\overrightarrow{OB}=2\overrightarrow{i}+3\overrightarrow{j}$; $\overrightarrow{OA}=2\overrightarrow{j}+5\overrightarrow{k}$;

Có $\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=\left(2\overrightarrow{i}+3\overrightarrow{j}\right)-\left(2\overrightarrow{j}+5\overrightarrow{k}\right)=2\overrightarrow{i}+\overrightarrow{j}-5\overrightarrow{k}$ .

2. Tọa độ của điểm và vectơ

Khám phá 2: Cho hình hộp chữ nhật OABC.O'A'B'C' có cạnh OA = 3, OC = 5, OO' = 2. Vẽ ba vectơ đơn vị $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$ lần lượt trên các cạnh OA, OC, OO'. Biểu diễn $\overrightarrow{O{B}^{\prime }}$ theo ba vectơ $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$ .

Trả lời:

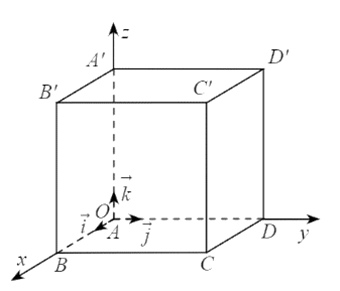
Thực hành 2: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 5. Chọn hệ trục tọa độ Oxyz có gốc O trùng với A; các điểm B, D, A' lần lượt nằm trên các tia Ox, Oy, Oz. Xác định tọa độ các điểm B, C, C'.

Trả lời:

Vì $\overrightarrow{OB}$ và $\overrightarrow{i}$ cùng hướng và OB = 5 nên $\overrightarrow{OB}=5\overrightarrow{i}$ .

Tương tự, ta có $\overrightarrow{OD}=5\overrightarrow{j};\overrightarrow{O{A}^{\prime }}=5\overrightarrow{k}$ .

Theo quy tắc hình bình hành, ta có: $\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}=5\overrightarrow{i}+5\overrightarrow{j}$ .

Theo quy tắc hình hộp, ta có: $\overrightarrow{O{C}^{\prime }}=\overrightarrow{OB}+\overrightarrow{OD}+\overrightarrow{O{A}^{\prime }}=5\overrightarrow{i}+5\overrightarrow{j}+5\overrightarrow{k}$ .

Do đó B(5; 0; 0), C(5; 5; 0), C'(5; 5; 5).

Khám phá 3: Trong không gian Oxyz, cho vectơ $\overrightarrow{a}$. Vẽ điểm A sao cho $\overrightarrow{OA}=\overrightarrow{a}$. Gọi $\left(a_1;a_2;a_3\right)$ là tọa độ của điểm A. Hãy biểu diễn $\overrightarrow{a}$ theo ba vectơ đơn vị $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$.

Trả lời:

Thực hành 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2, SA vuông góc với mặt phẳng đáy và có độ dài bằng 3 (Hình 11).

a) Vẽ hệ trục tọa độ Oxyz có gốc O trùng với điểm A, các điểm B, D, S lần lượt nằm trên các tia Ox, Oy, Oz và chỉ ra các vectơ đơn vị trên các trục tọa độ.

b) Trong hệ tọa độ nói trên, tìm tọa độ các vectơ $\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{AS}$ và $\overrightarrow{AM}$ với M là trung điểm của cạnh SC.

Trả lời:

a)

Ba vectơ đơn vị trên ba trục tọa độ lần lượt là $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$ với độ dài của $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$ lần lượt bằng $\frac{1}{2}AB,\frac{1}{2}AD,\frac{1}{3}AS$ .

b) Ta có: $\overrightarrow{AB}=2\overrightarrow{i};\overrightarrow{AD}=2\overrightarrow{j};\overrightarrow{AS}=3\overrightarrow{k}$ .

Do đó $\overrightarrow{AB}=\left(2;0;0\right)$ , $\overrightarrow{AD}=\left(0;2;0\right)$ , $\overrightarrow{AS}=\left(0;0;3\right)$ .

Theo quy tắc hình bình hành, ta có $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}=2\overrightarrow{i}+2\overrightarrow{j}$ .

Vì M là trung điểm của SC nên $\overrightarrow{AM}=\frac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{AS}\right)=\frac{1}{2}\left(2\overrightarrow{i}+2\overrightarrow{j}+3\overrightarrow{k}\right)$ $=\overrightarrow{i}+\overrightarrow{j}+\frac{3}{2}\overrightarrow{k}$ .

Do đó $\overrightarrow{AM}=\left(1;1;\frac{3}{2}\right)$.

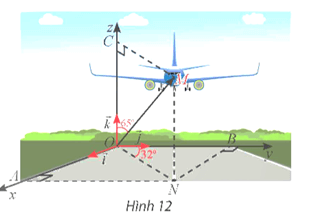
Vận dụng 2: Một máy bay đang cất cánh từ phi trường. Với hệ tọa độ Oxyz được thiết lập như Hình 12, cho biết M là vị trí của máy bay, OM = 14, $\widehat{NOB}=32°,\widehat{MOC}=65°$ . Tìm tọa độ điểm M.

Trả lời:

Xét tam giác  vuông tại  có ; 

.

Xét tam giác  vuông tại  có: 

;

Do đó, ta có . Từ đó suy ra tọa độ điểm  biểu diễn vị trí máy bay là 

Bài tập

Bài tập 1: Trong không gian Oxyz, biết

a) $\overrightarrow{a}=5\overrightarrow{i}+7\overrightarrow{j}-3\overrightarrow{k},\overrightarrow{b}=2\overrightarrow{i}+4\overrightarrow{k}$ . Tìm tọa độ các vectơ $\overrightarrow{a},\overrightarrow{b}$ .

b) $\overrightarrow{OM}=4\overrightarrow{i}-\overrightarrow{j}+3\overrightarrow{k},\overrightarrow{ON}=8\overrightarrow{i}-5\overrightarrow{j}$ . Tìm tọa độ điểm M, N.

Trả lời:

a) $\overrightarrow{a}=\left(5;7;-3\right),\overrightarrow{b}=\left(2;0;4\right)$.

b) $M=\left(4;-1;3\right),N\left(8;-5;0\right)$ .

Bài tập 2: Trong không gian Oxyz, biết:

a) $\overrightarrow{a}=\left(-2;5;-7\right)$, $\overrightarrow{b}=\left(4;0;1\right)$. Tính $\overrightarrow{a},\overrightarrow{b}$ theo các vectơ $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$ .

b) $A\left(7;-2;1\right),B\left(0;5;0\right)$ . Tính $\overrightarrow{OA},\overrightarrow{OB}$ theo các vectơ $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$ .

Trả lời:

a) 

b) 

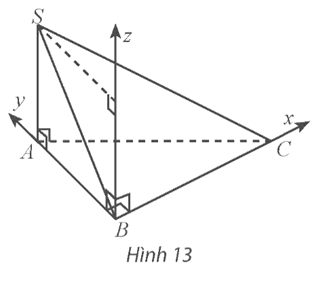
Bài tập 3: Cho tứ diện SABC có ABC là tam giác vuông tại B, BC = 3, BA = 2, SA vuông góc với mặt phẳng (ABC) và có độ dài bằng 2 (Hình 13).

a) Xác định một hệ tọa độ dựa trên gợi ý của hình vẽ và chỉ ra các vectơ đơn vị trên các trục tọa độ.

b) Tìm tọa độ các điểm A, B, C, S.

Trả lời:

a)

Các vectơ đơn vị trên ba trục Ox, Oy, Oz lần lượt là $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$với độ dài của $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$ lần lượt bằng $\frac{1}{3}BC,\frac{1}{2}BA,\frac{1}{2}SA$.

b) Vì B trùng với gốc tọa độ nên B(0; 0; 0).

Vì $\overrightarrow{j}$và $\overrightarrow{BA}$ cùng hướng và BA = 2 nên $\overrightarrow{BA}=2\overrightarrow{j}$. Suy ra A(0; 2; 0).

Vì $\overrightarrow{i}$và $\overrightarrow{BC}$ cùng hướng và BC = 3 nên $\overrightarrow{BC}=3\overrightarrow{i}$. Suy ra C(3; 0; 0).

Gọi E là hình chiếu của S lên trục Oz.

Ta có BE = AS = 2.

Vì $\overrightarrow{k}$và $\overrightarrow{BE}$ cùng hướng và BE = 2 nên $\overrightarrow{BE}=2\overrightarrow{k}$.

Theo quy tắc hình bình hành ta có:

$\overrightarrow{BS}=\overrightarrow{BA}+\overrightarrow{BE}=2\overrightarrow{j}+2\overrightarrow{k}$. Suy ra S(0; 2; 2).

Bài tập 4: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 2, SA vuông góc với đáy và SA bằng 1 (Hình 14). Thiết lập hệ tọa độ như hình vẽ, hãy vẽ các vectơ đơn vị trên các trục Ox, Oy, Oz và tìm tọa độ của các điểm A, B, C, S.

Trả lời:

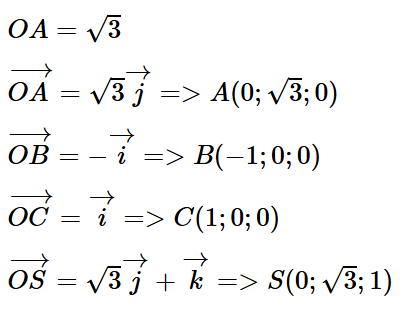
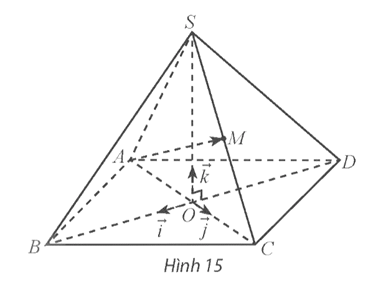
Bài tập 5: Trong không gian Oxyz, cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng 5, giao điểm hai đường chéo AC và BD trùng với gốc O. Các vectơ $\overrightarrow{OB},\overrightarrow{OC},\overrightarrow{OS}$ lần lượt cùng hướng với $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$ và $OA=OS=4$ (Hình 15). Tìm tọa độ các vectơ $\overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AS}$ và $\overrightarrow{AM}$  với M là trung điểm của cạnh SC.

Trả lời:

Vì ABCD là hình thoi cạnh bằng 5, O là giao điểm của AC và BD nên O là trung điểm của AC và BD.

Xét $\Delta$OAB vuông tại O, có $OB=\sqrt{A{B}^2-O{A}^2}=\sqrt{25-16}=3$.

Vì $\overrightarrow{OB}$ và $\overrightarrow{i}$cùng hướng và OB = 3 nên $\overrightarrow{OB}=3\overrightarrow{i}$.

Vì $\overrightarrow{OA}$ và $\overrightarrow{j}$cùng hướng và OA = 4 nên $\overrightarrow{OA}=-4\overrightarrow{j}$.

Ta có $\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=3\overrightarrow{i}+4\overrightarrow{j}$. Do đó $\overrightarrow{AB}=\left(3;4;0\right)$.

Có AC = 2OA = 8 mà $\overrightarrow{AC}$ và $\overrightarrow{j}$cùng hướng nên $\overrightarrow{AC}=8\overrightarrow{j}$. Do đó $\overrightarrow{AC}=\left(0;8;0\right)$.

Có $\overrightarrow{OS}$ và $\overrightarrow{k}$cùng hướng và OS = 4 nên $\overrightarrow{OS}=4\overrightarrow{k}$.

Có $\overrightarrow{SB}=\overrightarrow{OB}-\overrightarrow{OS}=3\overrightarrow{i}-4\overrightarrow{k}$. Do đó $\overrightarrow{SB}=\left(3;0;-4\right)$.

Lại có $\overrightarrow{AS}=\overrightarrow{AB}+\overrightarrow{BS}=\left(3\overrightarrow{i}+4\overrightarrow{j}\right)-\left(3\overrightarrow{i}-4\overrightarrow{k}\right)=4\overrightarrow{j}+4\overrightarrow{k}$. Do đó $\overrightarrow{AS}=\left(0;4;4\right)$.

Vì M là trung điểm của SC nên $\overrightarrow{AM}=\frac{1}{2}\left(\overrightarrow{AS}+\overrightarrow{AC}\right)$ $=\frac{1}{2}\left(4\overrightarrow{j}+4\overrightarrow{k}+8\overrightarrow{j}\right)=6\overrightarrow{j}+2\overrightarrow{k}$.

Do đó $\overrightarrow{AM}=\left(0;6;2\right)$.

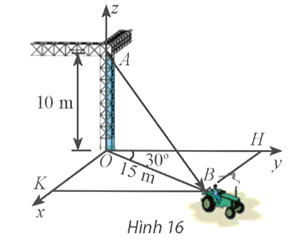
Bài tập 6: Một chiếc xe đang kéo căng sợi dây cáp AB trong công trường xây dựng, trên đó đã thiết lập hệ tọa độ Oxyz như Hình 16 với độ dài đơn vị trên các trục tọa độ bằng 1 m. Tìm tọa độ của vectơ $\overrightarrow{AB}$.

Trả lời:

Xét  vuông tại , có . 

Mà  nên 

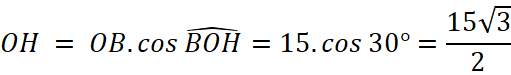
Suy ra:  nên 

Bài tập 7: Ở một sân bay, vị trí của máy bay được xác định bởi điểm M trong không gian Oxyz như Hình 17. Gọi H là hình chiếu vuông góc của M xuống mặt phẳng (Oxy). Cho biết OM = 50, $\left(\overrightarrow{i},\overrightarrow{OH}\right)=64°$, $\left(\overrightarrow{OH},\overrightarrow{OM}\right)=48°$. Tìm tọa độ của điểm M.

Trả lời:

Giả sử M(x; y; z).

H $\in$ (Oxy) $\Rightarrow$ H(x; y; 0).

Vì OBHA là hình bình hành nên BH = OA.

Vì OCMH là hình bình hành nên OC = MH.

Xét $\Delta$MHO vuông tại H, có OH = OM.cos48° = 50. cos48° ≈ 33,46.

MH = OM.sin48° = 50. sin48° ≈ 37,16.

Xét $\Delta$OAH vuông tại A, có BH = OA = OH.cos64° = 33,46. cos64° ≈ 14,67.

Xét $\Delta$OBH vuông tại B, có $OB=\sqrt{O{H}^2-B{H}^2}=\sqrt{33,{46}^2-14,{67}^2}\approx 30,07$ .

Vì $\overrightarrow{OA}$ và $\overrightarrow{i}$ cùng hướng và OA = 14,67 nên $\overrightarrow{OA}=14,67\overrightarrow{i}$ .

Vì $\overrightarrow{OB}$ và $\overrightarrow{j}$ cùng hướng và OB = 30,07 nên $\overrightarrow{OB}=30,07\overrightarrow{j}$ .

Vì $\overrightarrow{OC}$ và $\overrightarrow{k}$ cùng hướng và OC = 37,16 nên $\overrightarrow{OC}=37,16\overrightarrow{k}$ .

Áp dụng quy tắc hình bình hành, ta có:

$\overrightarrow{OM}=\overrightarrow{OH}+\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=14,67\overrightarrow{i}+30,07\overrightarrow{j}+27,16\overrightarrow{k}$

Vậy M(14,67; 30,07; 27,16).