Giải SGK Toán 12 Chân trời sáng tạo Bài tập cuối chương I

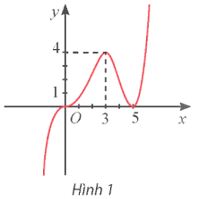
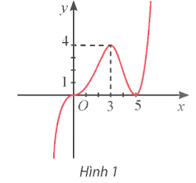
Bài tập 1: Cho hàm số y = f(x) có đồ thị như Hình 1. Hàm số y = f(x) đồng biến trên khoảng

A. (5; + ∞).

B. (3; 5).

C. (0; 5).

D. (3; + ∞).

Đáp án: A

Giải thích: Quan sát Hình 1, ta thấy trên khoảng (5; + ∞), đồ thị hàm số đi lên từ trái qua phải nên hàm số đồng biến trên khoảng đó.

Bài tập 2: Cho hàm số y = f(x) có đồ thị như Hình 1.

Hàm số đạt cực đại tại

A. x = 0.

B. x = 3.

C. x = 4.

D. x = 5.

Đáp án: B

Giải thích: Quan sát Hình 1, ta thấy trên khoảng (0; 3), đồ thị hàm số đi lên từ trái qua phải nên hàm số đồng biến trên khoảng đó, suy ra y' > 0 với x ∈ (0; 3); trên khoảng (3; 5) đồ thị hàm số đi xuống từ trái qua phải nên hàm số nghịch biến trên khoảng đó, suy ra y' < 0 với x ∈ (3; 5), vậy tại điểm x = 3, đạo hàm y' đổi dấu từ dương sang âm nên hàm số đạt cực đại tại điểm x = 3.

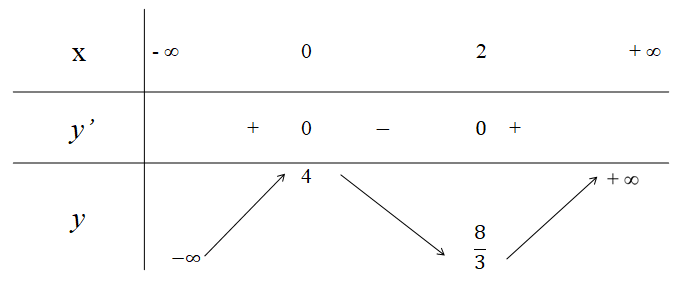
Bài tập 3: Cho hàm số $y=\frac{x^2-4x+1}{x-4}$. Trong các khẳng định sau, khẳng định nào đúng?

A. Hàm số đạt cực tiểu tại x = 3, giá trị cực tiểu là y = 2.

B. Hàm số đạt cực tiểu tại x = 5, giá trị cực tiểu là y = 6.

C. Hàm số đạt cực tiểu tại x = 3, giá trị cực tiểu là y = 6.

D. Hàm số đạt cực tiểu tại x = 5, giá trị cực tiểu là y = 2.

Đáp án: B

Giải thích:

Xét hàm số $y=\frac{x^2-4x+1}{x-4}$.

● Tập xác định: D = ℝ\{4}.

● Đạo hàm $y^{\prime }=\frac{\left(2x-4\right)\left(x-4\right)-x^2+4x-1}{{\left(x-4\right)}^2}=\frac{x^2-8x+15}{{\left(x-4\right)}^2}$.

Ta có y' = 0 ⇔ x = 3 hoặc x = 5.

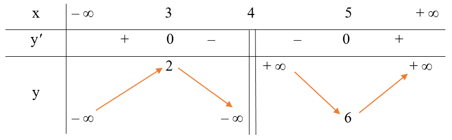
Bảng biến thiên:

Từ bảng biến thiên, suy ra hàm số đạt cực tiểu tại x = 5, giá trị cực tiểu là y = 6.

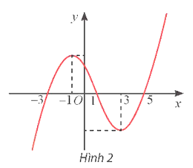
Bài tập 4: Đạo hàm của hàm số y = f(x) là hàm số có đồ thị được cho trong Hình 2. Hàm số y = f(x) nghịch biến trên khoảng

A. (– 1; 3).

B. (– 3; 1).

C. (1; 5).

D. (3; + ∞).

Đáp án: C

Giải thích:

- Đồ thị là của đạo hàm của f(x), tức là đồ thị của f'(x).

- Quan sát trên khoảng (1;5), thấy đồ thị của f'(x) nằm dưới trục hoành nên f'(x) < 0 trên khoảng (1;5).

- Do đó, hàm số nghịch biến trên khoảng (1;5).

Bài tập 5: Giá trị nhỏ nhất của hàm số $y=\sqrt{x^2+2x+3}$ trên đoạn [– 2; 3] là

A. $\sqrt{3}$.

B. $\sqrt{30}$.

C. $\sqrt{2}$.

D. 0.

Đáp án: C

Giải thích:

Xét hàm số $y=\sqrt{x^2+2x+3}$.

Tập xác định: D = ℝ.

Đạo hàm $y^{\prime }=\frac{x+1}{\sqrt{x^2+2x+3}}$. Trên khoảng (– 2; 3), y' = 0 khi x = – 1.

Ta có y(– 2) = $\sqrt{3}$, y(– 1) = $\sqrt{2}$, y(3) = $3\sqrt{2}$.

Vậy $\underset{\left[-2;3\right]}{\min }y=\sqrt{2}$ tại x = – 1.

Bài tập 6: Tiệm cận xiên của đồ thị hàm số $y=\frac{2x^3+3x^2-3}{x^2-1}$ là đường thẳng có phương trình

A.                                                 B. 

C.                                                    D. 

Đáp án: A

Giải thích:

Bài tập 7: Tiệm cận đứng của đồ thị hàm số $y=\frac{-2x+3}{5x+1}$ là đường thẳng có phương trình

A. $y=-\frac{1}{5}$.

B. $x=-\frac{1}{5}$.

C. $y=-\frac{2}{5}$.

D. $x=-\frac{2}{5}$.

Đáp án: B

Giải thích:

Xét hàm số $y=\frac{-2x+3}{5x+1}$.

Tập xác định D = $R\backslash \left\{-\frac{1}{5}\right\}$.

Ta có $\underset{x\to -{\frac{1}{5}}^{-}}{\lim }y=\underset{x\to -{\frac{1}{5}}^{-}}{\lim }\frac{-2x+3}{5x+1}=-\infty ;\underset{x\to -{\frac{1}{5}}^{+}}{\lim }y=\underset{x\to -{\frac{1}{5}}^{+}}{\lim }\frac{-2x+3}{5x+1}=+\infty$.

Vậy đường thẳng $x=-\frac{1}{5}$ là tiệm cận đứng của đồ thị hàm số $y=\frac{-2x+3}{5x+1}$

Bài tập 8: Cho hàm số $y=\frac{-2x-3}{4-x}$. Trong các khẳng định sau, khẳng định nào đúng?

A. Hàm số đồng biến trên (– ∞; – 4) và nghịch biến trên (– 4; + ∞).

B. Hàm số đồng biến trên (– ∞; 4) và (4; + ∞).

C. Hàm số nghịch biến trên (– ∞; 4) và (4; + ∞).

D. Hàm số nghịch biến trên (– ∞; – 4) và (– 4; + ∞).

Đáp án: C

Giải thích:

Xét hàm số $y=\frac{-2x-3}{4-x}$.

Tập xác định: D = ℝ\{4}.

Đạo hàm $y^{\prime }=\frac{-5}{{\left(4-x\right)}^2}$. Vì y' < 0 với mọi x ≠ 4 nên hàm số nghịch biến trên mỗi khoảng (– ∞; 4) và (4; + ∞).

Bài tập 9: Tìm hai số không âm a và b có tổng bằng 10 sao cho:

a) Biểu thức ab đạt giá trị lớn nhất;

b) Tổng các bình phương của chúng đạt giá trị nhỏ nhất;

c) Biểu thức ab2 đạt giá trị lớn nhất.

Trả lời:

Tập xác định: 

Đặt 

a) Ta có: 

Bảng biến thiên của hàm số trên đoạn 

Từ bảng biến thiên, hàm số có giá trị lớn nhất tại , khi đó 

b) Ta có: 

Bảng biến thiên của hàm số trên đoạn 

Từ bảng biến thiên, hàm số đạt giá trị nhỏ nhất tại , khi đó 

c) Ta có: 

;  hoặc  (loại)

Bảng biến thiên của hàm số trên đoạn 

Từ bảng biến thiên, hàm số đạt giá trị lớn nhất tại ; khi đó 

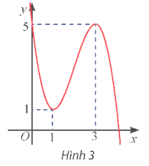
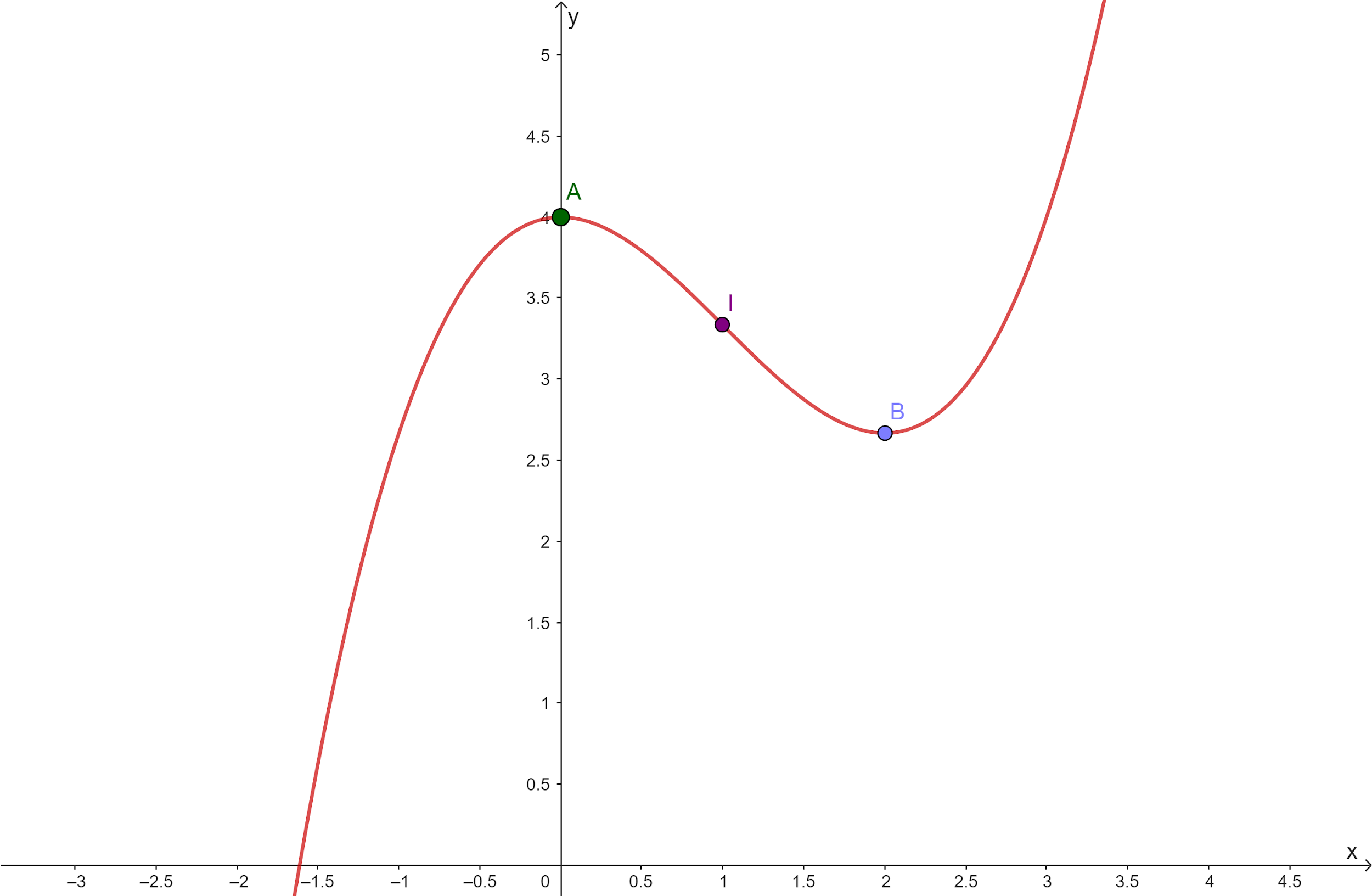
Bài tập 10: Cho hàm số bậc ba y = f(x) có đồ thị như Hình 3. Viết công thức của hàm số.

Trả lời:

Giả sử hàm số bậc ba cần tìm có dạng y = f(x) = ax3 + bx2 + cx + d (a ≠ 0).

Quan sát Hình 3, ta thấy đồ thị hàm số đi qua các điểm (0; 5), (1; 1) và (3; 5).

Với x = 0 thì y = 5, thay vào hàm số ta suy ra d = 5.

Khi đó hàm số trở thành y = f(x) = ax3 + bx2 + cx + 5.

Với x = 1 thì y = 1, thay vào hàm số ta được a + b + c + 5 = 1 (1).

Ta thấy đồ thị hàm số có hai điểm cực trị là (1; 1) và (3; 5), tức là phương trình y' = 0 có hai nghiệm là x = 1 và x = 3.

Ta có y' = 3ax2 + 2bx + c.

Với x = 1 thì y' = 0 nên ta có 3a + 2b + c = 0 (2).

Với x = 3 thì y' = 0 nên ta có 27a + 6b + c = 0 (3).

Từ (1), (2) và (3) ta suy ra a = – 1; b = 6; c = – 9.

Vậy hàm số cần tìm là y = f(x) = – x3 + 6x2 – 9x + 5.

Bài tập 11: Cho hàm số $y=\frac{1}{3}{x}^3-x^2+4$.

a) Khảo sát và vẽ đồ thị của hàm số.

b) Tính khoảng cách giữa hai điểm cực trị của đồ thị hàm số.

Trả lời:

a) 1. Tập xác định: 

2. Sự biến thiên: 

• Chiều biến thiên: 

Đạo hàm:  hoặc 

Trên các khoảng  và ,  nên hàm số đồng biến trên mỗi khoảng đó.

Trên khoảng ,  nên hàm số nghịch biến trên khoảng đó. 

• Cực trị:

Hàm số đạt cực đại tại 

Hàm số đạt cực tiểu tại 

• Các giới hạn tại vô cực: 

• Bảng biến thiên: 

3. Đồ thị: 

Khi  thì  nên  là giao điểm của đồ thị với trục . 

Ta có:  

Vậy đồ thị của hàm số giao với trục  tại hai điểm 

Điểm  là điểm cực đại và điểm là điểm cực tiểu của đồ thị hàm số. Đồ thị có tâm đối xứng là điểm 

b) 

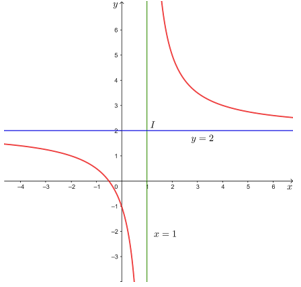
Bài tập 12: Cho hàm số $y=\frac{2x+1}{x-1}$.

a) Khảo sát và vẽ đồ thị của hàm số.

b) Gọi A là giao điểm của đồ thị hàm số với trục Oy, I là giao điểm của hai đường tiệm cận của đồ thị hàm số. Tìm điểm B đối xứng với A qua I. Chứng minh rằng điểm B cũng thuộc đồ thị hàm số này.

Trả lời:

a) Xét hàm số $y=\frac{2x+1}{x-1}$.

1. Tập xác định: D = ℝ\{1}.

2. Sự biến thiên:

● Chiều biến thiên:

Đạo hàm y' = $\frac{-3}{{\left(x-1\right)}^2}$. Vì y' < 0 với mọi x ≠ 1 nên hàm số nghịch biến trên mỗi khoảng (– ∞; 1) và (1; + ∞).

● Tiệm cận:

Ta có $\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\frac{2x+1}{x-1}=2;\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\frac{2x+1}{x-1}=2$. Suy ra đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.

Ta có $\underset{x\to 1^{-}}{\lim }y=\underset{x\to 1^{-}}{\lim }\frac{2x+1}{x-1}=-\infty ;\underset{x\to 1^{+}}{\lim }y=\underset{x\to 1^{+}}{\lim }\frac{2x+1}{x-1}=+\infty$. Suy ra đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.

● Bảng biến thiên:

3. Đồ thị:

Với x = 0 thì y = – 1 nên đồ thị hàm số giao với trục Oy tại điểm (0; – 1).

Với y = 0 thì x = $-\frac{1}{2}$ nên đồ thị hàm số giao với trục Ox tại điểm $\left(-\frac{1}{2};0\right)$.

Đồ thị của hàm số đã cho được biểu diễn như hình dưới đây.

Tâm đối xứng của đồ thị hàm số là điểm I(1; 2). Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận x = 1 và y = 2.

b) Ta có A(0; – 1), I(1; 2).

Vì B đối xứng với A qua I nên I là trung điểm của AB.

Khi đó, tọa độ của điểm B là $\{\begin{array}{c}{x}_B=2x_I-x_A=2\cdot 1-0=2\\ y_B=2y_I-y_A=2\cdot 2-\left(-1\right)=5\end{array}$. Suy ra B(2; 5).

Ta có $\frac{2\cdot 2+1}{2-1}=5$, do đó điểm B(2; 5) thuộc đồ thị hàm số $y=\frac{2x+1}{x-1}$.

Bài tập 13: Cho hàm số $y=\frac{x^2+4x-1}{x-1}$.

a) Khảo sát và vẽ đồ thị của hàm số.

b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [2; 4].

Trả lời:

a) 1. Tập xác định: 

2. Sự biến thiên:

• Chiều biến thiên: 

Đạo hàm  hoặc 

Trên các khoảng  và ,  nên hàm số đồng biến trên mỗi khoảng đó. 

Trên các khoảng  và ,  nên hàm số nghịch biến trên mỗi khoảng đó. 

• Cực trị: 

Hàm số đạt cực tiểu tại 

Hàm số đạt cực đại tạo 

• Các giới hạn tại vô cực, giới hạn vô cực và tiệm cận:

Ta có: ; 

Suy ra đường thẳng  là tiệm cận xiên của đồ thị hàm số.

Ta có:  ; .

Suy đường thẳng  là tiệm cận đứng của đồ thị hàm số.

• Bảng biến thiên: 

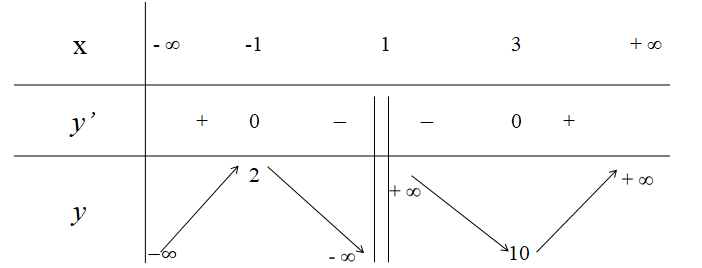
3. Đồ thị: 

Ta có:  hoặc 

Đồ thị của hàm số giao với trục  tại điểm ( và (

Tâm đối xứng của đồ thị là điểm .

Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận   và  .

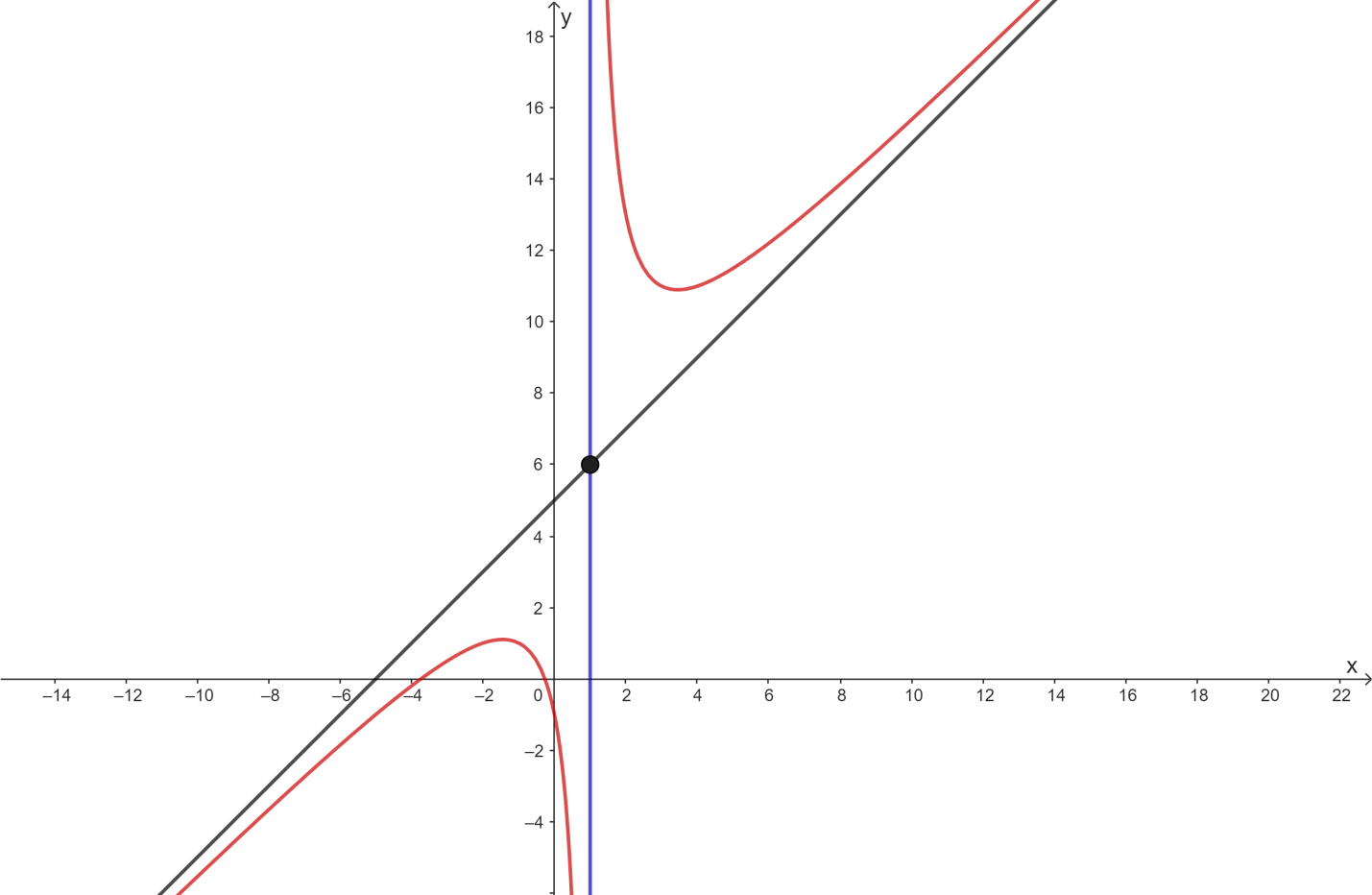
b) Ta có: 

Vậy trên đoạn , ; 

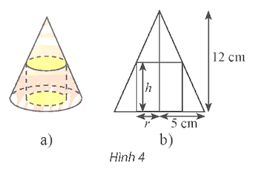
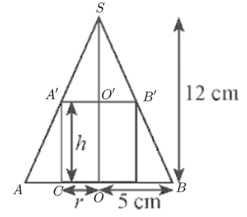
Bài tập 14: Cho một hình trụ nội tiếp trong hình nón có chiều cao bằng 12 cm và bán kính đáy bằng 5 cm (Hình 4a). Người ta cắt hình nón, trụ này theo mặt phẳng chứa đường thẳng nối đỉnh và tâm hình tròn đáy của hình nón thì thu được một hình phẳng như Hình 4b.

a) Chứng minh rằng công thức tính bán kính r của đáy hình trụ theo chiều cao h của nó là: $r=\frac{5\left(12-h\right)}{12}$.

b) Chứng minh biểu thức sau biểu thị thể tích khối trụ theo h: $V\left(h\right)=\frac{25\pi h{\left(12-h\right)}^2}{144}$.

c) Tìm h để khối trụ có thể tích lớn nhất.

Trả lời:

a) Ta đặt tên các điểm như hình vẽ dưới đây:

Ta có A'O' // AO nên $\frac{S{O}^{\prime }}{SO}=\frac{S{A}^{\prime }}{SA}$.

Lại có A'C // SO nên $\frac{S{A}^{\prime }}{SA}=\frac{OC}{OA}$.

Từ đó suy ra $\frac{S{O}^{\prime }}{SO}=\frac{OC}{OA}$.

Mà SO = 12 cm, OA = 5 cm, OC = r, SO' = SO – OO' = 12 – h.

Do đó, $\frac{12-h}{12}=\frac{r}{5}$. Suy ra $r=\frac{5\left(12-h\right)}{12}$.

b) Thể tích của khối trụ là V = πr2h = $\pi \cdot {\left[\frac{5\left(12-h\right)}{12}\right]}^2\cdot h=\frac{25\pi h{\left(12-h\right)}^2}{144}$(cm3).

Vậy thể tích khối trụ theo h là $V\left(h\right)=\frac{25\pi h{\left(12-h\right)}^2}{144}$.

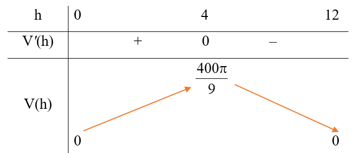
c) Rõ ràng h phải thỏa mãn điều kiện 0 < h < 12.

Xét hàm số $V\left(h\right)=\frac{25\pi h{\left(12-h\right)}^2}{144}$ với h ∈ (0; 12).

Ta có $V^{\prime }\left(h\right)=\frac{25\pi \left(12-h\right)\left(12-3h\right)}{144}$.

Trên khoảng (0; 12), ta có V'(h) = 0 khi h = 4.

Bảng biến thiên:

Căn cứ vào bảng biến thiên, ta thấy trên khoảng (0; 12), hàm số V(h) đạt giá trị lớn nhất bằng $\frac{400\pi }{9}$ tại h = 4.

Vậy h = 4 cm thì khối trụ có thể tích lớn nhất.