Giải SGK Toán 11 Kết nối tri thức Bài 1: Giá trị lượng giác của góc lượng giác - Giải SGK Toán 11 - Kết nối tri thức

Mở đầu

Câu hỏi mở đầu Toán 11 Kết nối tri thức Bài 1: Giá trị lượng giác của góc lượng giác: Trạm vũ trụ Quốc tế ISS (tên Tiếng Anh: International Space Station) nằm trong quỹ đạo tròn cách bề mặt Trái Đất khoảng 400 km (H.1.1). Nếu trạm mặt đất theo dõi được trạm vũ trụ ISS khi nó nằm trong góc 45° ở tâm của quỹ đạo tròn này phía trên ăng-ten theo dõi, thì trạm vũ trụ ISS đã di chuyển được bao nhiêu kilômét trong khi nó đang được trạm mặt đất theo dõi? Giả sử rằng bán kính của Trái Đất là 6 400 km. Làm tròn kết quả đến hàng đơn vị.

Trả lời:

Bán kính quỹ đạo của trạm vũ trụ quốc tế là R = 6 400 + 400 = 6 800 (km).

Đổi $45^{o}=45.\frac{\pi }{180}=\frac{\pi }{4}=rad$

Vậy trong khi được trạm mặt đất theo dõi, trạm ISS đã di chuyển một quãng đường có độ dài là:

l = Rα = $6800.\frac{\pi }{4}\approx 5340,708\approx 5341(km)$

1. Góc lượng giác

a. Khái niệm góc lượng giác và số đo của góc lượng giác

Hoạt động 1: Trên đồng hồ Hình 1.2, kim phút đang chỉ đúng số 2

a) Phải quay kim phút mấy phần của một vòng tròn theo chiều quay ngược chiều kim đồng hồ để nó chỉ đúng số 12?

b) Phải quay kim phút mấy phần của một vòng tròn theo chiều quay của kim đồng hồ để nó chỉ đúng số 12?

c) Có bao nhiêu cách quay kim phút theo một chiều xác định để kim phút từ vị trí chỉ đúng số 2 về vị trí chỉ đúng số 12?

Trả lời:

a) Trên đồng hồ ở Hình 1.2, kim phút đang chỉ đúng số 2, để nó chỉ đúng số 12 khi quay kim phút theo chiều quay ngược chiều kim đồng hồ thì ta phải quay kim phút từ vị trí số 2 đến vị trí số 12 theo chiều ngược chiều kim đồng hồ, nghĩa là quay kim phút một khoảng bằng $\frac{2}{12}=\frac{1}{6}$ vòng tròn.

b) Trên đồng hồ ở Hình 1.2, kim phút đang chỉ đúng số 2, để nó chỉ đúng số 12 khi quay kim phút theo chiều quay của chiều kim đồng hồ thì ta phải quay kim phút từ vị trí số 2 đến vị trí số 12 theo chiều quay của kim đồng hồ, nghĩa là quay kim phút một khoảng bằng $\frac{10}{12}=\frac{5}{6}$ vòng tròn.

c) Có 2 cách quay kim phút theo một chiều xác định để kim phút từ vị trí chỉ đúng số 2 về vị trí chỉ đúng số 12, đó là: ngược chiều kim đồng hồ và cùng chiều kim đồng hồ

Luyện tập 1: Cho góc hình học $\widehat{uOv}=45^{\circ}$ . Xác định số đo của góc lượng giác (Ou, Ov) trong mỗi trường hợp sau:

Trả lời:

Ta có:

- Góc lượng giác tia đầu Ou, tia cuối Ov, quay theo chiều dương có số đo là: sđ(Ou, Ov) = 45°.

- Góc lượng giác có tia đầu Ou, tia cuối Ov, quay theo chiều âm có số đo là: sđ(Ou, Ov) = – (360° – 45°) = – 315°.

b. Hệ thức Chasles

Hoạt động 2: Cho ba tia Ou, Ov, Ow với số đo của các góc hình học uOv và vOw lần lượt là $30^{\circ}$ và $45^{\circ}$

a) Xác định số đo của ba góc lượng giác $(O u, O v)$ , $(O v, O w$ và $(O u, O w)$ được chỉ ra ở Hình 1.5.

b) Với các góc lượng giác ở câu a, chứng tỏ rằng có một số nguyên k để (Ou,Ov) + sđ(Ov, Ow) = sđ (Ou,Ow) + k360^o $k\epsilon \mathbb{Z}$

Trả lời:

a) Ta có:

- Các góc lượng giác tia đầu Ou, tia cuối Ov có số đo là: sđ $(O u, O v) = 30^{\circ} + n {.360}^{\circ}$

- Các góc lượng giác tia đầu Ov, tia cuối Ow có số đo là: sđ $(O v, O w) = 45^{\circ} + m {.360}^{\circ}$

- Các góc lượng giác tia đầu Ou, tia cuối Ow có số đo là: sđ $(O u, O w) = 75^{\circ} + k {.360}^{\circ}$

b) Ta có: sđ(Ou, Ov) + sđ(Ov, Ow) = 30° + 45° = 75°.

Lại có: – 285° + 1 x 360° = 75°.

Vậy tồn tại một số nguyên k = 1 để sđ(Ou, Ov) + sđ(Ov, Ow) = sđ(Ou, Ow) + k360°.

Luyện tập 2: Cho một góc lượng giác (Ox, Ou) có số đo 240° và một góc lượng giác (Ox, Ov) có số đo – 270°. Tính số đo của các góc lượng giác (Ou, Ov).

Trả lời:

Số đo của các góc lượng giác tia đầu Ou, tia cuối Ov là: sđ(Ou, Ov) = sđ(Ox, Ov) – sđ(Ox, Ou) + k360°

= – 270° – 240° + k360° = – 510° + k360°

= 210° – 720° + k360° = 210° + (k – 2)360°

= 210° + m360° (m = k – 2, m ∈ ℤ).

=> Vậy các góc lượng giác (Ou, Ov) có số đo là 210° + m360° (m ∈ ℤ).

2. Đơn vị đo góc và độ dài cung vòng

a. Đơn vị đo góc và cung vòng

Luyện tập 3:

a) Đổi từ độ sang rađian các số đo sau: $360^{\circ}, - 450^{\circ}$

b) Đổi từ rađian sang độ các số đo sau: $3\pi ,-\frac{11\pi }{5}$

Trả lời:

a) $360^{\circ}=360.\frac{\pi }{180}=2\pi -450^{\circ}=450.\frac{\pi }{180}=\frac{5}{2}\pi$

b) $3\pi =3\pi .(\frac{180}{\pi })^{\circ}=540^{\circ}-\frac{11\pi }{5}=(\frac{-11\pi }{5}).(\frac{180}{\pi })^{\circ}=-396^{\circ}$

b. Độ dài cung tròn

Hoạt động 3: Cho đường tròn bán kính R.

a) Độ dài của cung tròn có số đo bằng 1 rad là bao nhiêu?

b) Tính độ dài l của cung tròn có số đo $α$

Trả lời:

a) Cung tròn có số đo bằng 1 rad nếu độ dài của nó đúng bằng bán kính R. Do đó, độ dài của cung tròn có số đo bằng 1 rad là R.

b) Độ dài l của cung tròn có số đo $α$ $α$ rad: l = $\mathbb{R\alpha }$

Vận dụng 1: Giải bài toán ở tình huống mở đầu

Trả lời:

(Xem lời giải ở mục mở đầu)

3. Giá trị lượng giác của góc lượng giác

a. Đường tròn lượng giác

Hoạt động 4: Trong mặt phẳng tọa độ Oxy, vẽ đường tròn tâm O bán kính R = 1. Chọn điểm gốc của đường tròn là giao điểm A(1; 0) của đường tròn với trục Ox. Ta quy ước chiều dương của đường tròn là chiều ngược chiều quay của kim đồng hồ và chiều âm là chiều quay của kim đồng hồ.

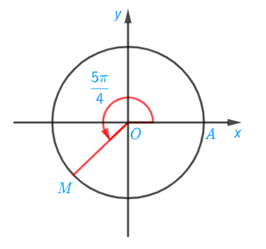
a) Xác định điểm M trên đường tròn sao cho sđ(OA, OM) = $\frac{5\pi }{4}$

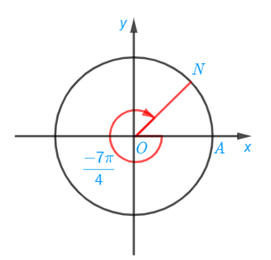
b) Xác định điểm N trên đường tròn sao cho sđ(OA, ON) = $\frac{-7\pi }{4}$

Trả lời:

a) Ta có: sđ(OA, OM) = $\frac{5\pi }{4}=\pi +\frac{\pi }{4}$

Điểm M trên đường tròn sao cho sđ(OA, OM) = $\frac{5\pi }{4}$ được xác định như trên hình vẽ dưới đây:

b) Điểm N trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng $\frac{-7\pi }{4}$ được xác định là điểm chính giữa cung BA.

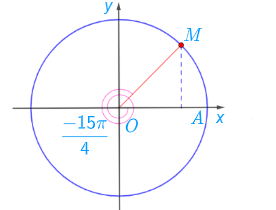
Luyện tập 4: Xác định điểm M và N trên đường tròn lượng giác lần lượt biểu diễn các góc lượng giác có số đo bằng $-\frac{15\pi }{4}$ và 420^o

Trả lời:

- Điểm biểu diễn góc lượng giác có số đo bằng $-\frac{15\pi }{4}=-\frac{-7}{4}+(-1).2\pi$ được xác định là điểm M.

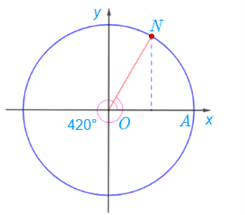
- Ta có: 420° = 60° + 360°, điểm N trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng 420° được xác định trong hình dưới đây:

b. Các giá trị lượng giác của góc lượng giác

Hoạt động 5: Nhắc lại khái niệm các giá trị lượng giác sin α, cos α, tan α, cot α của góc α (0° ≤ α ≤ 180°) đã học ở lớp 10 (H.1.9a).

Trả lời:

- Với mỗi góc α (0° ≤ α ≤ 180°), gọi M(x₀; y₀) là điểm trên nửa đường tròn đơn vị sao cho $\widehat{xOM}=\alpha$

+ sin của góc α là tung độ y₀ của điểm M, kí hiệu là sin α (sin α = y₀).

+ côsin của góc α là hoành độ của x₀ của điểm M, kí hiệu là cos α (cos α = x₀).

+ Khi α ≠ 90° (hay là x0 ≠ 0), tang của α là $\frac{y_{o}}{x_{o}}$ , kí hiệu là tan α ( $tan \alpha =\frac{sin\alpha }{cos\alpha }=\frac{y_{o}}{x_{o}}$ )

+ Khi α ≠ 0° và α ≠ 180° (hay là y0 ≠ 0), côtang của α là $\frac{y_{o}}{x_{o}}$ , kí hiệu là cot α. ( $cos\alpha =\frac{cos\alpha }{sin\alpha }=\frac{y_{o}}{x_{o}}$ ).

Luyện tập 5: Cho góc lượng giác có số đo bằng $\frac{5\pi }{6}$

a) Xác định điểm M trên đường tròn lượng giác biểu diễn góc lượng giác đã cho.

b) Tính các giá trị lượng giác của góc lượng giác đã cho.

Trả lời:

a) Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó điểm M là điểm biểu diễn bởi góc có số đo $\frac{5\pi }{6}$

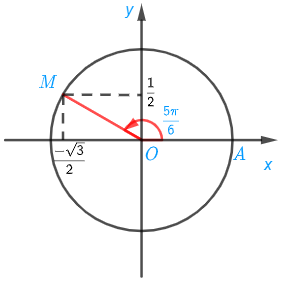
b) Ta có:

$cos\frac{5\pi }{6}=-\frac{\sqrt{3}}{2}; sin \frac{5\pi }{6}=\frac{1}{2}$

$tan\frac{5\pi }{6}=\frac{sin\frac{5\pi }{6}}{cos\frac{5\pi }{6}}=-\frac{\sqrt{3}}{3}; cot\frac{5\pi }{6}=\frac{cos\frac{5\pi }{6}}{sin\frac{5\pi }{6}}=-\sqrt{3}$

c. Giá trị lượng giác của các góc đặc biệt

d. Sử dụng máy tính cầm tay để đổi số đo góc và tìm giá trị lượng giác của góc

Luyện tập 6: Sử dụng máy tính cầm tay để:

a) Tính: $cos\frac{3\pi }{7}; tan(37^{\circ}25')$

b) Đổi 179^o23'30" sang rađian

c) Đổi $\frac{7}{9}$ (rad) sang độ

Trả lời:

a) cos $\frac{3\pi }{7}$ $\cos \frac{3 π}{7} = 0, 22252$ ; $\tan (- 37^{\circ} 25^{'}) = 0, 765018$

b) Đổi 179°23'30" sang rađian (màn hình hiện 3,130975234) => 179°23'30" ≈ 3,130975234 (rad).

c) $\frac{7\pi }{9}=140^{\circ}$

4. Quan hệ giữa các giá trị lượng giác

a. Các công thức lượng giác cơ bản

Hoạt động 6:

a) Dựa vào định nghĩa của sin α và cos α, hãy tính sin² α + cos² α.

b) Sử dụng kết quả của HĐ6a và định nghĩa của tan α, hãy tính 1 + tan² α.

Trả lời:

a) Theo định nghĩa, ta có: sin α = y, cos α = x.

Do đó, sin² α + cos2 α = (sin α)² + (cos α)² = y² + x².

Từ hình vẽ ta thấy x² + y² = R² = 1 (theo định lí Pythagore và đường tròn đơn vị có bán kính R = 1).

Vậy sin² α + cos²α = 1.

b) $1 + tan^{2}\alpha =\frac{cos^{2}\alpha }{cos^{2}\alpha }+\frac{sin^{2}\alpha }{cos^{2}\alpha }=\frac{1}{cos^{2}\alpha }$

Luyện tập 7: Tính các giá trị lượng giác của góc α, biết: cos α = $\alpha =-\frac{2}{3}$ và $\pi <\alpha <\frac{3\pi }{2}$

Trả lời:

Vì $\pi <\alpha <\frac{3\pi }{2}$ nên sinα < 0. Mặt khác, từ sin² α + cos² α = 1 suy ra:

$sin\alpha =-\sqrt{1-cos^{2}\alpha }=\sqrt{1-(-\frac{2}{3})^{2}}=-\frac{\sqrt{5}}{3}$

Do đó, $tan\alpha =\frac{sin\alpha }{cos\alpha }=\frac{-\frac{\sqrt{5}}{3}}{-\frac{2}{3}}=\frac{\sqrt{5}}{2}$ và $cot\alpha =\frac{1}{tan\alpha }=\frac{1}{\frac{\sqrt{5}}{2}}=\frac{2}{\sqrt{5}}=\frac{2\sqrt{5}}{5}$

b. Giá trị lượng giác của các góc có liên quan đặc biệt

Hoạt động 7: Xét hai điểm M, N trên đường tròn lượng giác xác định bởi hai góc đối nhau (H1.12a).

a) Có nhận xét gì về vị trí của hai điểm M, N đối với hệ trục Oxy. Từ đó rút ra liên hệ giữa: cos (– α) và cos α; sin (– α) và sin α.

b) Từ kết quả HĐ7a, rút ra liên hệ giữa: tan (– α) và tan α; cot (– α) và cot α.

Trả lời:

a) Giả sử M(x_M; y_M), N(x_N; y_N).

Từ Hình 1.12a, ta thấy hai điểm M và N đối xứng với nhau qua trục hoành Ox, do đó ta có: x_M = x_N và y_M = – y_N.

Theo định nghĩa giá trị lượng giác của một góc, ta lại có:

cos α = x_M và cos (– α) = x_N. Suy ra cos (– α) = cos α.

sin α = y_M và sin (– α) = y_N. Suy ra sin α = – sin (– α) hay sin (– α) = – sin α.

b) Ta có: $\tan (- α)$

Luyện tập 8: Tính

a) sin(-675^o)

b) $tan\frac{15\pi }{4}$

Trả lời:

a) sin(– 675°) = sin(45° – 2 . 360°) = sin 45° = $\frac{\sqrt{2}}{2}$

b) $tan\frac{15\pi }{4}=tan(3\pi +\frac{3\pi }{4})=tan\frac{3\pi }{4}=tan(\pi -\frac{\pi }{4})=-tan(\frac{\pi }{4})=-1$

Vận dụng 2: Huyết áp của mỗi người thay đổi trong ngày. Giả sử huyết áp tâm trương (tức là áp lực máu lên thành động mạch khi tim giãn ra) của một người nào đó ở trạng thái nghỉ ngơi tại thời điểm t được cho bởi công thức: $B(t)=80+7sin\frac{\pi \tau }{12}$ trong đó t là số giờ tính từ lúc nửa đêm và B(t) tính bằng mmHg (milimét thủy ngân). Tìm huyết áp tâm trương của người này vào các thời điểm sau:

a) 6 giờ sáng;

b) 10 giờ 30 phút sáng;

c) 12 giờ trưa;

d) 8 giờ tối.

Trả lời:

a) Thời điểm 6 giờ sáng, tức t = 6, khi đó: $B(6)=80+7sin\frac{6\pi }{12}=87$

b) Thời điểm 10 giờ 30 phút sáng tức t=10,5, khi đó: $B(10,5)=80+7.sin\frac{\pi 10,5}{12}=80+7.sin\frac{7\pi }{8}=82,67878$

c) Thời điểm 12 giờ trưa tức t = 12 khi đó: $B(12)=80+7sin\frac{12\pi }{12}=80$

d) Thời điểm 8 giờ tối hay 20 giờ, tức t = 20, khi đó: $B(20)=80+7sin\frac{20\pi }{12}=\frac{160-7\sqrt{3}}{2}$