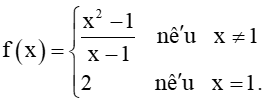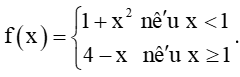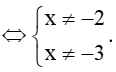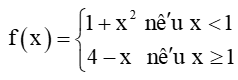Giải SGK Toán 11 Kết nối tri thức Bài 17: Hàm số liên tục

Mở đầu: Một người lái xe từ địa điểm A đến địa điểm B trong thời gian 3 giờ. Biết quãng đường từ A đến B dài 180 km. Chứng tỏ rằng có ít nhất một thời điểm trên hành trình, xe chạy với vận tốc 60 km/h.

Trả lời:

Theo giả thiết, vận tốc trung bình của xe là va = $\frac{180}{3}$ = 60(km/h).

Gọi v(t) là hàm biểu thị vận tốc của xe tại thời điểm t.

Tại thời điểm xuất phát t0, vận tốc của xe v(t0) = 0 nên có một thời điểm t1 xe chạy với vận tốc v(t1) > va.

Xét hàm số f(t) = v(t) – va, rõ ràng f(t) là hàm số liên tục trên đoạn [t0; t1].

Hơn nữa, ta có f(t0) = – va < 0, f(t1) = v(t1) – va > 0 (do v(t1) > va), nên tồn tại thời điểm t* thuộc khoảng (t0; t1) sao cho f(t*) = 0. Khi đó ta có v(t*) – va = 0 hay v(t*) = va = 60.

1. Hàm số liên tục tại một điểm

Hoạt động 1: Nhận biết tính liên tục của hàm số tại một điểm

Cho hàm số 

Tìm giới hạn $\underset{x\to 1}{\lim }f\left(x\right)$ và so sánh giá trị này với f(1).

Trả lời:

limx→1x2−1x−1=limx→1(x+1)=2

f(1) = 2

Suy ra limx→1f(x)=f(1)

Luyện tập 1: Xét tính liên tục của hàm số 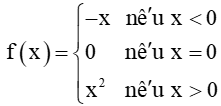 tại điểm x0 = 0.

Trả lời:

Hàm số f(x) xác định trên ℝ, do đó x0 = 0 thuộc tập xác định của hàm số.

Ta có: $\underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{+}}{\lim }{x}^2=0^2=0$; $\underset{x\to 0^{-}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }\left(-x\right)=0$.

Do đó, $\underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }f\left(x\right)=0$, suy ra $\underset{x\to 0}{\lim }f\left(x\right)=0$.

Lại có f(0) = 0 nên $\underset{x\to 0}{\lim }f\left(x\right)=f\left(0\right)$. Vậy hàm số f(x) liên tục tại x0 = 0.

2. Hàm số liên tục trên một khoảng

Hoạt động 2: Cho hai hàm số f(x)={2xnếu0≤x121nếu12<x≤1 và g(x)={xnếu0≤x121nếu12<x≤1 với đồ thị tương ứng như Hình 5.7

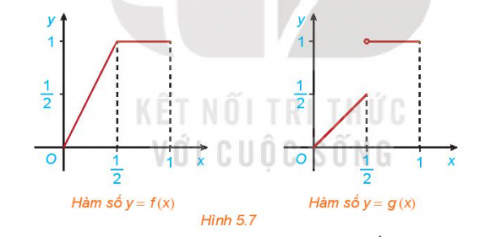
Xét tính liên tục của các hàm số f(x) và g(x) tại điểm x=12 và nhận xét sụ khác nhau giữa hai đồ thị

Trả lời:

limx→(12)−f(x)=limx→(12)−2x=1

limx→(12)+f(x)=limx→(12)−1=1

f(12)=2×12=1

Vậy f(x) liên tục tại x=12

limx→(12)−g(x)=limx→(12)−x=12

limx→(12)+f(x)=limx→(12)−1=1

f(12)=12=

Vậy g(x) gián đoạn tại x=12

Đồ thị f(x) liên tục trên đoạn [0,1], đồ thị g(x) bị gián đoạn tại x=12

Luyện tập 2: Tìm các khoảng trên đó hàm số $f\left(x\right)=\frac{x^2+1}{x+2}$ liên tục.

Trả lời:

Biểu thức $\frac{x^2+1}{x+2}$ có nghĩa khi x + 2 ≠ 0 hay x ≠ – 2.

Do đó, tập xác định của hàm số f(x) là (–∞; – 2) ∪ (– 2; +∞).

Vậy hàm số f(x) liên tục trên các khoảng (–∞; – 2) và (– 2; +∞).

3. Một số tính chất cơ bản

Hoạt động 3: Cho hai hàm số f(x) = x2 và g(x) = – x + 1.

a) Xét tính liên tục của hai hàm số trên tại x = 1.

b) Tính  và so sánh L với f(1) + g(1).

Trả lời:

a) Hàm số f(x) = x2 và g(x) = – x + 1 là các hàm đa thức nên nó liên tục trên ℝ.

Do đó, hai hàm số f(x) và g(x) đều liên tục tại x = 1.

b) f(1)+g(1)=1+0=1

limx→1[f(x)+g(x)]=limx→1(x2−x+1)=1

limx→1[f(x)+g(x)]=f(1)+g(1)

Vận dụng: Giải bài toán ở tình huống mở đầu.

Trả lời:

Theo giả thiết, vận tốc trung bình của xe là va = $\frac{160}{3}$ = 60 (km/h).

Gọi v(t) là hàm biểu thị vận tốc của xe tại thời điểm t.

Tại thời điểm xuất phát t0, vận tốc của xe v(t0) = 0 nên có một thời điểm t1 xe chạy với vận tốc v(t1) > va.

Xét hàm số f(t) = v(t) – va, rõ ràng f(t) là hàm số liên tục trên đoạn [t0; t1].

Hơn nữa, ta có f(t0) = – va < 0, f(t1) = v(t1) – va > 0 (do v(t1) > va), nên tồn tại thời điểm t* thuộc khoảng (t0; t1) sao cho f(t*) = 0. Khi đó ta có v(t*) – va = 0 hay v(t*) = va = 60.

Vậy có ít nhất một thời điểm trên hành trình, xe chạy với vận tốc 60 km/h.

Bài tập

Bài 5.14: Cho f(x) và g(x) là các hàm số liên tục tại x = 1. Biết f(1) = 2 và . Tính g(1).

Trả lời:

Vì f(x) và g(x) liên tục tại x = 1 suy ra 2f(1)−g(1)=limx→1[2f(x)−g(x)]=3 

=> Suy ra g(1)=1

Bài 5.15: Xét tính liên tục của các hàm số sau trên tập xác định của chúng:

a) $f\left(x\right)=\frac{x}{x^2+5x+6}$;

b) 

Trả lời:

a) $f\left(x\right)=\frac{x}{x^2+5x+6}$

Biểu thức $\frac{x}{x^2+5x+6}$ có nghĩa khi x2 + 5x + 6 ≠ 0 ⇔ (x + 2)(x + 3) ≠ 0 

Do đó, tập xác định của hàm số f(x) là ℝ \ {– 3; – 2} = (–∞; – 3) ∪ (– 3; – 2) ∪ (– 2; +∞).

Vì f(x) là hàm phân thức hữu tỉ nên nó liên tục trên tập xác định.

Vậy hàm số f(x) liên tục trên các khoảng (–∞; – 3), (– 3; – 2) và (– 2; +∞).

b) 

Tập xác định của hàm số là ℝ.

+) Nếu x < 1, thì f(x) = 1 + x2.

Đây là hàm đa thức nên có tập xác định là ℝ.

Vậy nó liên tục trên (–∞; 1).

+) Nếu x > 1, thì f(x) = 4 – x.

Đây là hàm đa thức nên có tập xác định là ℝ.

Vậy nó liên tục trên (1; +∞).

+) Ta có: $\underset{x\to 1^{+}}{\lim }f\left(x\right)=\underset{x\to 1^{+}}{\lim }\left(4-x\right)=4-1=3$;

$\underset{x\to 1^{-}}{\lim }f\left(x\right)=\underset{x\to 1^{-}}{\lim }\left(1+x^2\right)=1+1^2=2$.

Suy ra $\underset{x\to 1^{+}}{\lim }f\left(x\right)\ne \underset{x\to 1^{-}}{\lim }f\left(x\right)$, do đó không tồn tại giới hạn của f(x) tại x = 1.

Khi đó, hàm số f(x) không liên tục tại x = 1.

Vậy hàm số đã cho liên tục trên các khoảng (–∞; 1), (1; +∞) và gián đoạn tại x = 1.

Bài 5.16: Tìm giá trị của tham số m để hàm số f(x)={sinxnếux≥0−x+mnếux<0 liên tục trên R

Trả lời:

Ta có: limx→0+sinx=0

Để hàm số liên tục trên R thì limx→0+sinx=limx→0−(−x+m)=0⇒m=0

Bài 5.17: Một bảng giá cước taxi được cho như sau:

a) Viết công thức hàm số mô tả số tiền khách phải trả theo quãng đường di chuyển.

b) Xét tính liên tục của hàm số ở câu a.

Trả lời:

a) Gọi x (km, x > 0) là quãng đường khách di chuyển và y (đồng) là số tiền khách phải trả theo quãng đường di chuyển x.

Với x ≤ 0,5, ta có y = 10 000.

Với 0,5 < x ≤ 30, ta có: y = 10 000 + 13 500(x – 0,5) hay y = 13 500x + 3 250.

Với x > 30, ta có: y = 10 000 + 13 500 . 29,5 + 11 000(x – 30) hay y = 11 000x + 78 250.

Vậy công thức hàm số mô tả số tiền khách phải trả theo quãng đường di chuyển là

b) +) Với 0 < x < 0,5 thì y = 10 000 là hàm hằng nên nó liên tục trên (0; 0,5).

+) Với 0,5 < x < 30 thì y = 13500x + 3 250 là hàm đa thức nên nó liên tục trên (0,5; 30).

+) Với x > 30 thì y = 11 000x + 78 250 là hàm đa thức nên nó liên tục trên (30; +∞).

+) Ta xét tính liên tục của hàm số tại x = 0,5 và x = 30.

- Tại x = 0,5, ta có y(0,5) = 10 000;

$\underset{x\to 0,5^{-}}{\lim }y=\underset{x\to 0,5^{-}}{\lim }10000=10000$;

$\underset{x\to 0,5^{+}}{\lim }y=\underset{x\to 0,5^{+}}{\lim }\left(13500x+3250\right)$= 13 500 . 0,5 + 3 250 = 10 000.

Do đó, $\underset{x\to 0,5^{-}}{\lim }y=\underset{x\to 0,5^{+}}{\lim }y=\underset{x\to 0,5}{\lim }y=y\left(0,5\right)$ nên hàm số liên tục tại x = 0,5.

- Tại x = 30, ta có: y(30) = 13 500 . 30 + 3 250 = 408 250;

$\underset{x\to {30}^{-}}{\lim }y=\underset{x\to {30}^{-}}{\lim }\left(13500x+3250\right)$ = 13 500 . 30 + 3 250 = 408 250;

$\underset{x\to {30}^{+}}{\lim }y=\underset{x\to {30}^{+}}{\lim }\left(11000x+78250\right)$ = 11 000 . 30 + 78 250 = 408 250.

Do đó, $\underset{x\to {30}^{-}}{\lim }y=\underset{x\to {30}^{+}}{\lim }y=\underset{x\to 30}{\lim }y=y\left(30\right)$ nên hàm số liên tục tại x = 30.

Vậy hàm số ở câu a liên tục trên (0; +∞).