Hoạt động khởi động: Khi được thả từ độ cao 20 m, một vật rơi với gia tốc không đổi a = 10 m/s2. Sau khi rơi được t giây thì vật có tốc độ bao nhiêu và đi được quãng đường bao nhiêu?
Lời giải:
Sau khi học xong bài này, ta sẽ giải quyết bài toán này như sau:
Kí hiệu v(t) là tốc độ của vật, s(t) là quãng đường vật đi được cho đến thời điểm t giây kể từ khi vật bắt đầu rơi.
Vì a(t) = v'(t) với mọi t ≥ 0 nên .
Vì v(0) = 0 nên C = 0. Vậy v(t) = 10t (m/s).
Vì v(t) = s'(t) với mọi t ≥ 0 nên .
Ta có s(0) = 0 nên C = 0. Vậy s(t) = 5t2 (m).
Vật rơi từ độ cao 20 m nên s(t) ≤ 20, suy ra 0 ≤ t ≤ 2.
Vậy sau khi vật rơi được t giây (0 ≤ t ≤ 2) thì vật có tốc độ v(t) = 10t m/s và đi được quãng đường s(t) = 5t2 mét.
1. Khái niệm nguyên hàm
Hoạt động khám phá 1: Cho hàm số f(x) = 2x xác định trên ℝ. Tìm một hàm số F(x) sao cho F'(x) = f(x).
Lời giải:
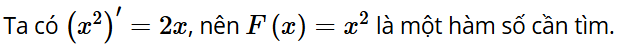
Hoạt động khám phá 2: Cho hàm số f(x) = 3x2 xác định trên ℝ.
a) Chứng minh rằng F(x) = x3 là một nguyên hàm của f(x) trên ℝ.
b) Với C là hằng số tùy ý, hàm số H(x) = F(x) + C có là nguyên hàm của f(x) trên ℝ không?
c) Giả sử G(x) là một nguyên hàm của f(x) trên ℝ. Tìm đạo hàm của hàm số G(x) – F(x). Từ đó, có nhận xét gì về hàm số G(x) – F(x)?
Lời giải:
a) ![]() với mọi
với mọi ![]() thuộc
thuộc ![]() .
.
Vậy ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() trên
trên ![]()
b) ![]()
Khi đó ![]() với mọi
với mọi ![]() thuộc
thuộc ![]() .
.
Vậy ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() trên
trên ![]()
c) Vì ![]() là một nguyên hàm của
là một nguyên hàm của ![]() trên
trên ![]() nên
nên ![]()
![]()
Vậy đạo hàm của hàm số ![]() bằng
bằng ![]() ; suy ra hàm số
; suy ra hàm số ![]() là một hằng số.
là một hằng số.
Thực hành 1: Chứng minh rằng F(x) = e2x + 1 là một nguyên hàm của hàm số f(x) = 2e2x + 1 trên ℝ.
Lời giải:
Có F'(x) = (e2x + 1)' = e2x + 1.(2x + 1)' = 2e2x + 1 = f(x).
Vậy F(x) = e2x + 1 là một nguyên hàm của hàm số f(x) = 2e2x + 1 trên ℝ.
2. Nguyên hàm của một số hàm số sơ cấp
Hoạt động khám phá 3:
a) Giải thích tại sao và .
b) Tìm đạo hàm của hàm số . Từ đó, tìm .
Lời giải:
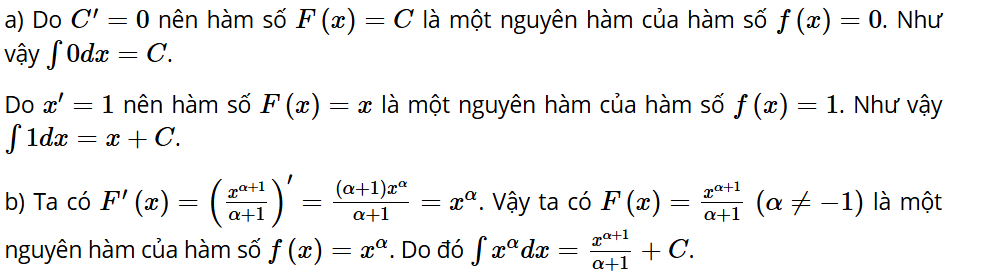
Thực hành 2: Tìm:
a) ; b) ; c) .
Lời giải:
a)
b)
c)
Hoạt động khám phá 4: Cho hàm số F(x) = ln|x| với x ≠ 0.
a) Tìm đạo hàm của F(x).
b) Từ đó, tìm .
Lời giải:
a) Với ![]() thì
thì ![]() nên
nên ![]()
Với ![]() thì
thì ![]() nên
nên ![]()
![]() với
với ![]()
b) Vì ![]() với mọi
với mọi ![]() thuộc
thuộc ![]() nên
nên ![]() là một nguyên hàm của
là một nguyên hàm của ![]() trên
trên ![]()
![]()
Hoạt động khám phá 5:
a) Tìm đạo hàm của các hàm số y = sinx, y = −cosx, y = tanx, y = −cotx.
b) Từ đó, tìm và
Lời giải:
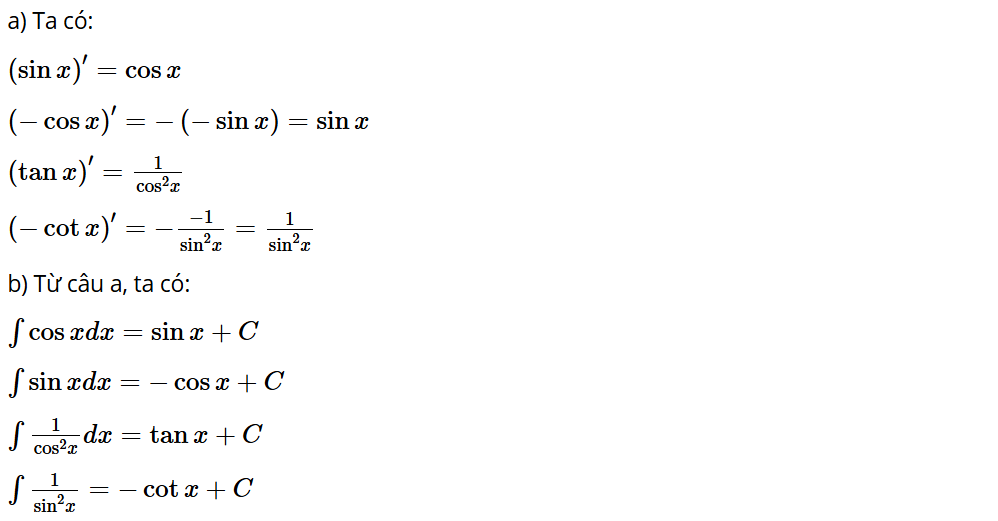
Thực hành 3: Tìm nguyên hàm F(x) của hàm số f(x) = cosx thỏa mãn .
Lời giải:
![]()
Với ![]() ta có:
ta có: ![]()
Với ![]() ta có:
ta có: ![]()
![]()
![]()
Hoạt động khám phá 6:
a) Tìm đạo hàm của các hàm số y = ex, với a > 0, a ≠ 1.
b) Từ đó, tìm và (a > 0, a ≠ 1).
Lời giải:
a) Có (ex)' = ex, , a > 0, a ≠ 1.
b) .
, (a > 0, a ≠ 1).
Thực hành 4: Tìm:
a)
b)
Lời giải:
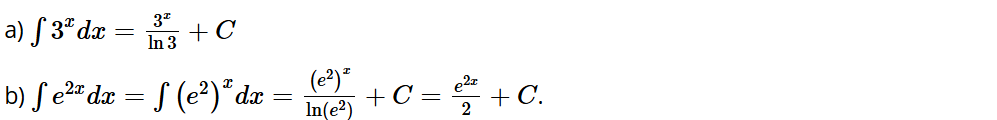
3. Tính chất cơ bản của nguyên hàm
Hoạt động khám phá 7: Ta có và (x3)' = 3x2.
a) Tìm và .
b) Tìm .
c) Từ các kết quả trên, giải thích tại sao .
Lời giải:
a) ; .
b) .
c) .
Thực hành 5: Tìm:
a) .
b)
Lời giải:
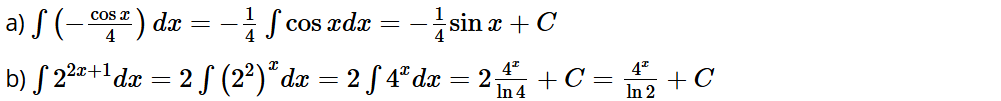
Hoạt động khám phá 8: Ta có , (x2)' = 2x và .
a) Tìm và .
b) Tìm .
c) Từ các kết quả trên, giải thích tại sao .
Lời giải:


Thực hành 6: Tìm:
a) ; b)
Lời giải:
a) .
b)
Thực hành 7: Một ô tô đang chạy với tốc độ 19 m/s thì hãm phanh và chuyển động chậm dần với tốc độ v(t) = 19 – 2t (m/s). Kể từ khi hãm phanh, quãng đường ô tô đi được sau 1 giây, 2 giây, 3 giây là bao nhiêu?
Lời giải:

Bài tập
Bài tập 1: Tính đạo hàm của hàm số F(x) = xex, suy ra nguyên hàm của hàm số f(x) = (x + 1)ex
Lời giải:
Có F'(x) = (xex)' = ex + xex = (1 + x)ex.
Do đó .
Bài tập 2: Tìm:
a) ; b) ; c) ; d)
Lời giải:
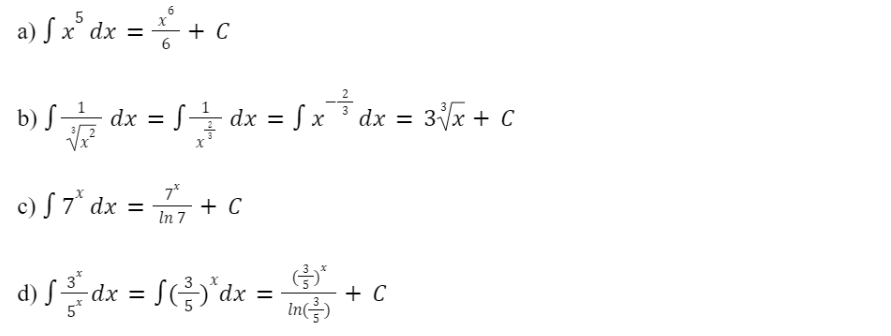
Bài tập 3: Tìm nguyên hàm F(x) của hàm số thỏa mãn
Lời giải:
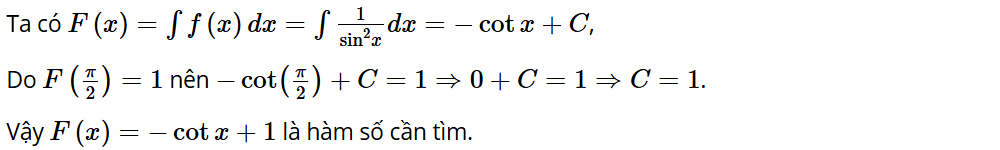
Bài tập 4: Tìm:
a) ; b) ;
c) ; d)
Lời giải:
a) .
b) .
c) .
d) .
Bài tập 5: Tìm:
a) ; b) ;
c) ; d)
Lời giải:
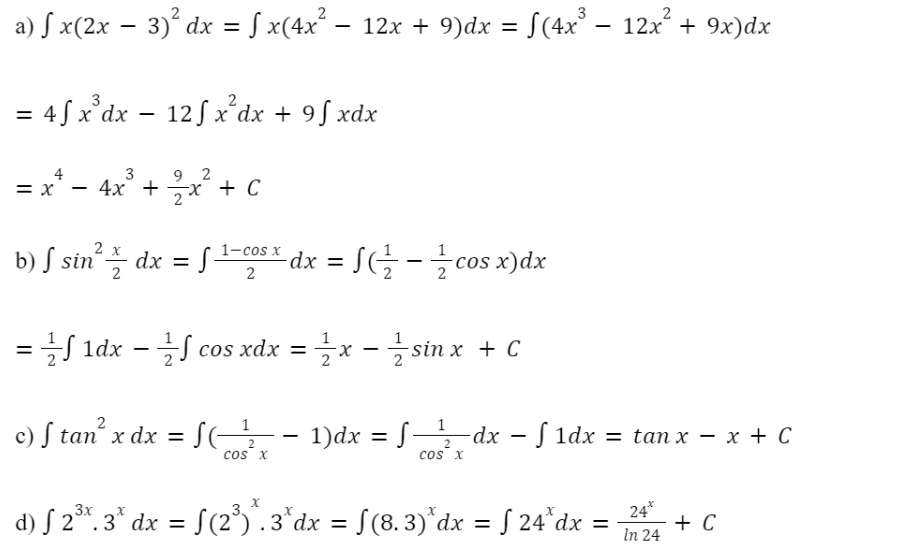
Bài tập 6: Kí hiệu h(x) là chiều cao của một cây (tính theo mét) sau khi trồng x năm. Biết rằng sau năm đầu tiên cây cao 2 m. Trong 10 năm tiếp theo, cây phát triển với tốc độ (m/năm).
a) Xác định chiều cao của cây sau x năm (1 ≤ x ≤ 11).
b) Sau bao nhiêu năm cây cao 3 m?
Lời giải:

Bài tập 7: Một chiếc xe đang chuyển động với vận tốc v0 = 10 m/s thì tăng tốc với gia tốc không đổi a = 2 m/s2. Tính quãng đường xe đó đi được trong 3 giây kể từ khi bắt đầu tăng tốc.
Lời giải:
Kí hiệu  là tốc độ của xe,
là tốc độ của xe, 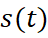 là quãng đường xe đó đi được sau t giây tăng tốc
là quãng đường xe đó đi được sau t giây tăng tốc
Do chọn mốc thời gian tính từ lúc xe bắt đầu tăng tốc nên 
Vì 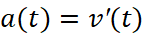 với mọi
với mọi 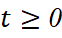 nên:
nên:
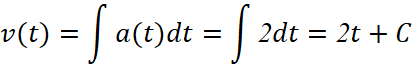
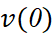 = 10 m/s nên
= 10 m/s nên 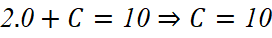
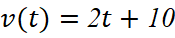 (m/s)
(m/s)
Vì 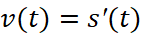 với mọi
với mọi 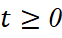 nên:
nên:
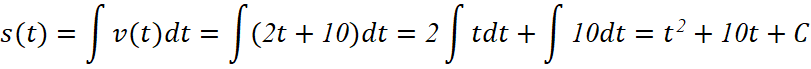
Mà 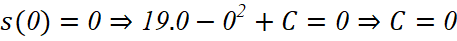
y 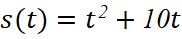
Vậy quãng đường xe đó đi được trong 3 giây kể từ khi bắt đầu tăng tốc là:
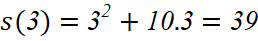 (m)
(m)
