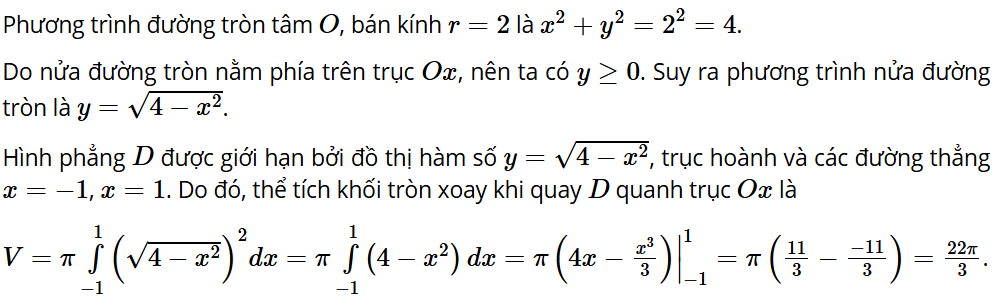Giải SGK Toán 12 Chân trời sáng tạo Bài tập cuối chương IV

Câu hỏi trắc nghiệm

Bài tập 1: Hàm số nào sau đây là một nguyên hàm của hàm số y = x4?

A. $-\frac{x^5}{5}$.

B. 4x3.

C. $\frac{x^5}{5}+1$.

D. −4x3 – 1.

Đáp án: C

Vì ${\left(\frac{x^5}{5}+1\right)}^{\prime }=x^4$ nên hàm số $y=\frac{x^5}{5}+1$ là một nguyên hàm của hàm số y = x4.

Bài tập 2: Hàm số nào sau đây là một nguyên hàm của hàm số $y=\frac{1}{x^2}$?

A. $\frac{1}{x^3}$

B. $-\frac{1}{x}$

C. $\frac{1}{x}$

D. $-\frac{1}{x^3}$

Đáp án: B

Bài tập 3: Khẳng định nào sau đây đúng?

A. $\int \left(\cos x-2\sin x\right)dx=\sin x+2\cos x+C$

B. $\int \left(\cos x-2\sin x\right)dx=-\sin x+2\cos x+C$

C. $\int \left(\cos x-2\sin x\right)dx=\sin x-2\cos x+C$

D. $\int \left(\cos x-2\sin x\right)dx=-\sin x-2\cos x+C$

Đáp án: A.

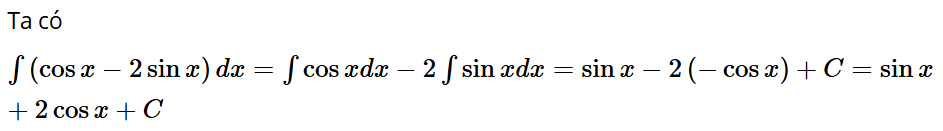
Bài tập 4: Khẳng định nào sau đây đúng?

A. $\int {\left(x-\frac{1}{x}\right)}^{2}dx=\frac{x^3}{3}-2x-\frac{1}{x}+C$

B. $\int {\left(x-\frac{1}{x}\right)}^{2}dx=\frac{x^3}{3}-2x+\frac{1}{x}+C$

C. $\int {\left(x-\frac{1}{x}\right)}^{2}dx=\frac{1}{3}{\left(x-\frac{1}{x}\right)}^3+C$

D. $\int {\left(x-\frac{1}{x}\right)}^{2}dx=\frac{1}{3}{\left(x-\frac{1}{x}\right)}^3\left(1+\frac{1}{x^2}\right)+C$

Đáp án: A.

Ta có $\int {\left(x-\frac{1}{x}\right)}^{2}dx=\int \left(x^2-2+\frac{1}{x^2}\right)dx=\frac{x^3}{3}-2x-\frac{1}{x}+C$

Bài tập 5: Khẳng định nào sau đây đúng?

A. $\int 3^{2x}dx=\frac{9^x}{\ln 9}+C$

B. $\int 3^{2x}dx=9^x.\ln 9+C$

C. $\int 3^{2x}dx={\left(\frac{3^x}{\ln 3}\right)}^2+C$

D. $\int 3^{2x}dx=3^x.\ln 3+C$

Đáp án: A.

Bài tập 6: Giá trị của $\underset{-2}{\overset{1}{\int }}\left(4x^3+3x^2+8x\right)dx+\underset{1}{\overset{2}{\int }}\left(4x^3+3x^2+8x\right)dx$ bằng

A. 16.

B. −16.

C. 52.

D. 0.

Đáp án: A

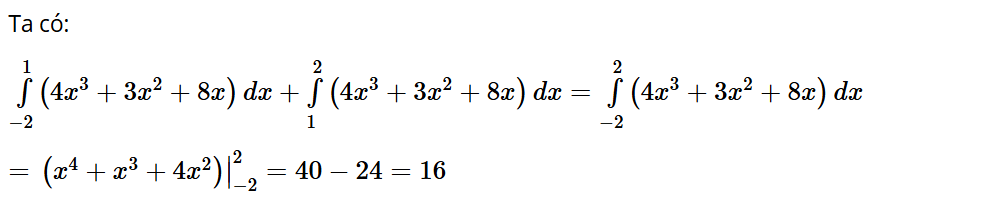
Bài tập 7: Biết rằng $\underset{0}{\overset{2}{\int }}f\left(x\right)dx=-4$. Giá trị của $\underset{0}{\overset{2}{\int }}\left[3x-2f\left(x\right)\right]dx$ bằng

A. −2.

B. 12.

C. 14.

D. 22.

Đáp án: C

Ta có $\underset{0}{\overset{2}{\int }}\left[3x-2f\left(x\right)\right]dx=3\underset{0}{\overset{2}{\int }}xdx-2\underset{0}{\overset{2}{\int }}f\left(x\right)dx$$={\frac{3x^2}{2}|}_0^2-2\left(-4\right)=14$

Bài tập 8: Giá trị của $\underset{0}{\overset{2}{\int }}\left|x^2-x\right|dx$ bằng

A. $\frac{2}{3}$.

B. 1.

C. $\frac{1}{3}$.

D. 2.

Đáp án: B

  hoặc  đều 

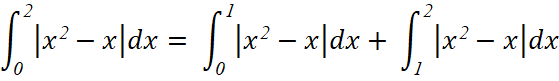
Bài tập 9: Diện tích của hình phẳng giới hạn bởi đồ thị của hai hàm số y = x3, y = x và hai đường thẳng x = 0, x = 2 bằng

A. 2.

B. $\frac{5}{2}$.

C. $\frac{9}{4}$.

D. $\frac{1}{4}$.

Đáp án: B

Diện tích cần tính là: $S=\underset{0}{\overset{2}{\int }}\left|x^3-x\right|dx$

Có x3 – x = 0 ⇔ x = 0 hoặc x =1 hoặc x = −1.

Với x ∈ [0; 1] thì x3 – x ≤ 0, x ∈ [1; 2] thì x3 – x ≥ 0.

Do đó $S=\underset{0}{\overset{1}{\int }}\left|x^3-x\right|dx+\underset{1}{\overset{2}{\int }}\left|x^3-x\right|dx$$=\underset{0}{\overset{1}{\int }}\left(x-x^3\right)dx+\underset{1}{\overset{2}{\int }}\left(x^3-x\right)dx$

$={\left(\frac{x^2}{2}-\frac{x^4}{4}\right)|}_0^1+{\left(\frac{x^4}{4}-\frac{x^2}{2}\right)|}_1^2$$=\frac{1}{4}+2+\frac{1}{4}=\frac{5}{2}$

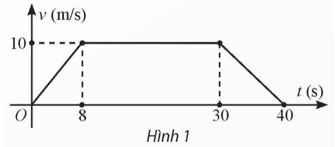
Bài tập 10: Tốc độ chuyển động v (m/s) của một ca nô trong khoảng thời gian 40 giây được thể hiện như Hình 1. Quãng đường đi được của ca nô trong khoảng thời gian này là

A. 400 m.

B. 350 m.

C. 310 m.

D. 200 m.

Đáp án: C

Bài tập 11: Cho D là hình phẳng giới hạn bởi đồ thị hàm số $y=\sqrt{x+1}$, trục tung, trục hoành và đường thẳng x = 2. Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành bằng

A. 6π.

B. 2π.

C. 3π.

D. 4π.

Đáp án: D

Thể tích cần tìm là:

$V=\pi \underset{0}{\overset{2}{\int }}\left(x+1\right)dx$$={\pi \left(\frac{x^2}{2}+x\right)|}_0^2=4\pi$

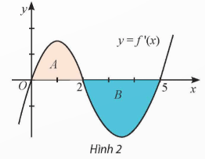
Bài tập 12: Cho hàm số y = f(x). Đồ thị của đạo hàm y = f'(x) là đường cong trong Hình 2. Biết rằng diện tích của các phần hình phẳng A và B lần lượt là SA = 2 và SB = 3. Nếu f(0) = 4 thì f(5) bằng

A. 3.

B. 5.

C. 9.

D. −1.

Đáp án: A

Bài tập tự luận

Bài tập 13: Tìm:

a) $\int \left[4{\left(2-3x\right)}^2-3\cos x\right]dx$;                     b) $\int \left(3x^3-\frac{1}{2x^3}\right)dx$;

c) $\int \left(\frac{2}{{\sin }^{2}x}-\frac{1}{3{\cos }^{2}x}\right)dx$;                         d) $\int \left(3^{2x-2}+4\cos x\right)dx$;

e) $\int \left(4\sqrt[5]{5x^4}+\frac{3}{\sqrt{x^3}}\right)dx$;                              g) $\int {\left(\sin \frac{x}{2}-\cos \frac{x}{2}\right)}^{2}dx$.

Lời giải:

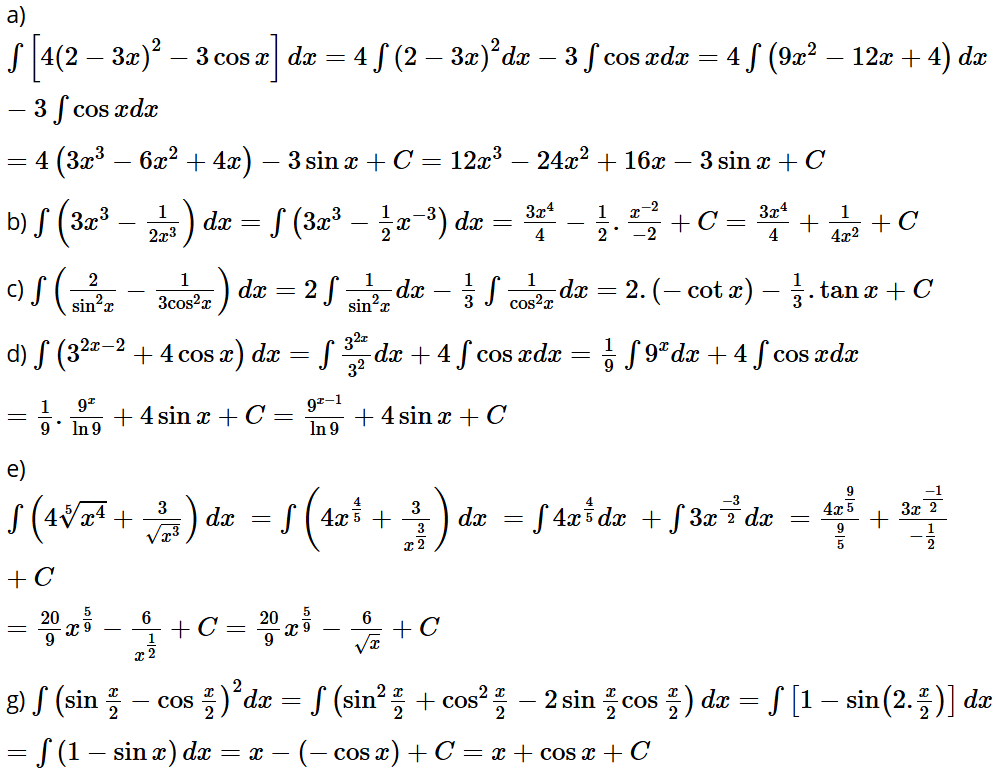
Bài tập 14: Tính đạo hàm của $F\left(x\right)=\ln \left(x+\sqrt{x^2+1}\right)$. Từ đó suy ra nguyên hàm của $f\left(x\right)=\frac{1}{\sqrt{x^2+1}}$.

Lời giải:

Vì  với  nên  là một nguyên hàm của 

Do đó 

Bài tập 15: Cho f(x) = x2 lnx và g(x) = xlnx. Tính f'(x) và $\int g\left(x\right)dx$

Lời giải:

Có f'(x) = (x2lnx)' = 2xlnx + x = 2g(x) + x.

Suy ra $g\left(x\right)=\frac{f^{\prime }\left(x\right)}{2}-\frac{x}{2}$,

Ta có $\int g\left(x\right)dx=\int \left(\frac{f^{\prime }\left(x\right)}{2}-\frac{x}{2}\right)dx$$=\frac{1}{2}\int f^{\prime }\left(x\right)dx-\frac{1}{2}\int xdx$$=\frac{1}{2}.f\left(x\right)-\frac{x^2}{4}+C$

$=\frac{x^2}{2}\ln x-\frac{x^2}{4}+C$

Bài tập 16: Tính các tích phân sau:

a) $\underset{0}{\overset{1}{\int }}\left(4x^3+x\right)dx$;                                      b) $\underset{1}{\overset{2}{\int }}\frac{x-2}{x^2}dx$;

c) $\underset{0}{\overset{4}{\int }}{2}^{2x}dx$;                                                d) $\underset{1}{\overset{2}{\int }}\left(e^{x-1}+2^{x+1}\right)dx$

Lời giải:

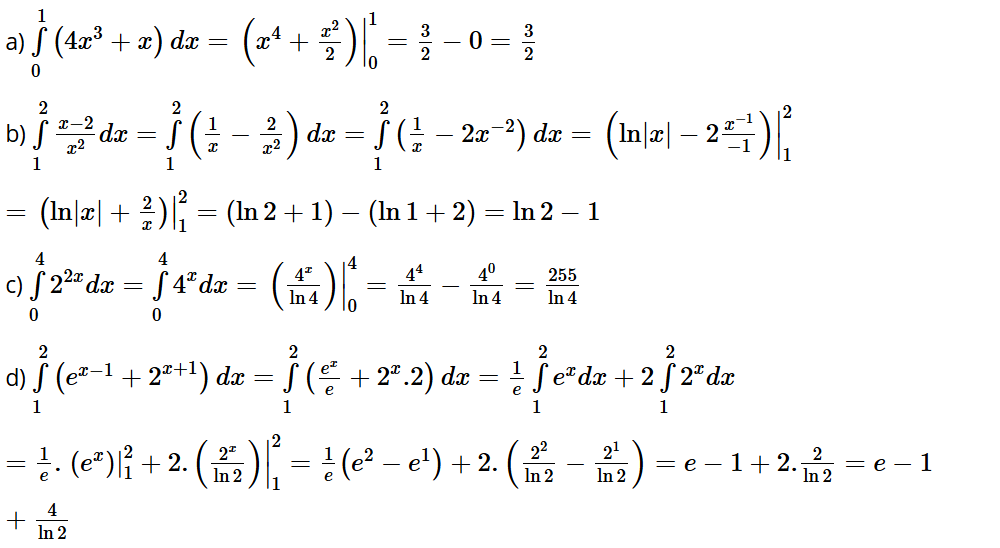
Bài tập 17: Tính các tích phân sau:

a) $\underset{\frac{\pi }{6}}{\overset{\frac{\pi }{4}}{\int }}\frac{1}{{\sin }^{2}x}dx$;                                           b) $\underset{0}{\overset{\frac{\pi }{4}}{\int }}\left(1+\tan x\right)\cos xdx$.

Lời giải:

a) 

b) 

Bài tập 18: Một vật chuyển động với tốc độ v(t) = 3t + 4 (m/s), với thời gian t tính theo giây, t ∈ [0; 5]. Tính quãng đường vật đi được trong khoảng thời gian từ t = 0 đến t = 5.

Lời giải:

Quãng đường vật đi được trong khoảng thời gian từ t = 0 đến t = 5 là:

$s=\underset{0}{\overset{5}{\int }}v\left(t\right)dt=\underset{0}{\overset{5}{\int }}\left(3t+4\right)dt={\left(3\frac{t^2}{2}+4t\right)|}_0^5=\mathrm{57,5}$m

Bài tập 19: Một chất điểm đang chuyển động với tốc độ v0 = 1 m/s thì tăng tốc với gia tốc không đổi a = 3 m/s2. Hỏi tốc độ của chất điểm là bao nhiêu sau 10 giây kể từ khi bắt đầu tăng tốc.

Lời giải:

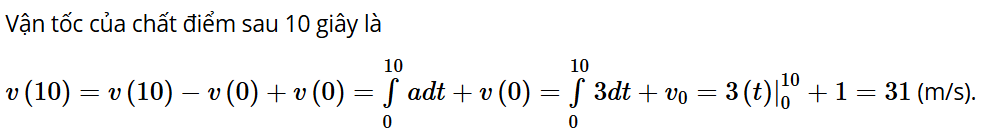
Bài tập 20: Tốc độ tăng dân số của một thành phố trong một số năm được ước lượng bởi công thức P'(t) = 20.(1,106)t với 0 ≤ t ≤ 7, trong đó t là thời gian tính theo năm và t = 0 ứng với đầu năm 2015, P(t) là dân số của thành phố tính theo nghìn người. Cho biết dân số của thành phố đầu năm 2015 là 1008 nghìn người.

a) Tính dân số của thành phố ở thời điểm đầu năm 2020 (làm tròn đến nghìn người).

b) Tính tốc độ tăng dân số trung bình hằng năm của thành phố trong giai đoạn từ đầu năm 2015 đến đầu năm 2020.

Lời giải:

 (nghìn người)

=> 

a) 

Vậy dân số của thành phố ở thời điểm đầu năm 2020 là:

 nghìn người

b) Tốc độ tăng dân số trung bình hằng năm của thành phố trong giai đoạn từ đầu năm 2015 đến đầu năm 2020 là:

 nghìn người/ năm

Bài tập 21: Sau khi được thả rơi tự do từ độ cao 100 m, một vật rơi xuống với tốc độ v(t) = 10t (m/s), trong đó t là thời gian tính theo giây kể từ khi thả vật.

a) Tính quãng đường s(t) vật di chuyển được sau thời gian t giây (trong khoảng thời gian vật đang rơi).

b) Sau bao nhiêu giây thì vật chạm đất? Tính tốc độ rơi trung bình của vật.

Lời giải:

a) Quãng đường s(t) vật di chuyển được sau thời gian t giây là:

$s\left(t\right)=\int v\left(t\right)dt=\int 10tdt=5t^2+C$.

Vì s(0) = 0 nên C = 0.

Do đó s(t) = 5t2 .

b) Vật chạm đất khi s(t) = 100 ⇔ 5t2 = 100 => $t=2\sqrt{5}$(vì t > 0).

Vậy vật chạm đất sau $2\sqrt{5}\approx \mathrm{4,47}$ giây.

Tốc độ rơi trung bình là $\frac{1}{2\sqrt{5}}\underset{0}{\overset{2\sqrt{5}}{\int }}10tdt=\frac{1}{2\sqrt{5}}.{5t^2|}_0^{2\sqrt{5}}=10\sqrt{5}$ m/s

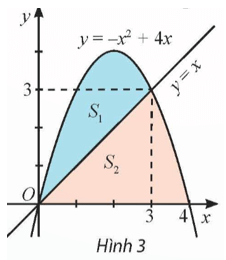
Bài tập 22: Cho S1, S2 là diện tích các hình phẳng được mô tả trong Hình 3. Tính $\frac{S_1}{S_2}$.

Lời giải:

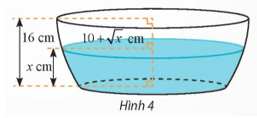
Bài tập 23: Nếu cắt chậu nước có hình dạng như Hình 4 bằng mặt phẳng song song và cách mặt đáy x (cm), (0 ≤ x ≤ 16) thì mặt cắt là hình tròn có bán kính $\left(10+\sqrt{x}\right)$ (cm). Tính dung tích của chậu.

Lời giải:

Chọn trục  vuông góc với 2 mặt của chậu nước, sao cho 2 mặt nằm trong 2 mặt phẳng  và 

Mặt nước vuông góc với trục  tại điểm có hoành độ   cắt chậu nước theo mặt cắt có diện tích không đổi:

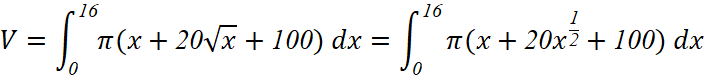
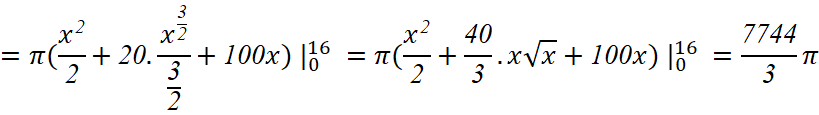
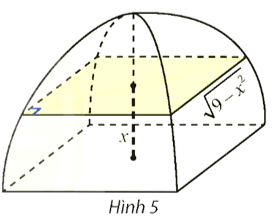
Bài tập 24: Một chiếc lều mái vòm có hình dạng như Hình 5. Nếu cắt lều bằng mặt phẳng song song với mặt đáy và cách mặt đáy một khoảng x (m) (0 ≤ x ≤ 3) thì được hình vuông có cạnh $\sqrt{9-x^2}$(m). Tính thể tích của lều.

Lời giải:

Diện tích mặt cắt là: $S\left(x\right)=\left(9-x^2\right)$(m2).

Thể tích của lều là: $V=\underset{0}{\overset{3}{\int }}\left(9-x^2\right)dx$$={\left(9x-\frac{x^3}{3}\right)|}_0^3=18.$

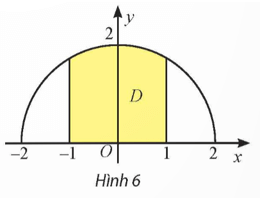
Bài tập 25: Trên mặt phẳng tọa độ Oxy, vẽ nửa đường tròn tâm O, bán kính r = 2 nằm phía trên trục Ox. Gọi D là hình phẳng giới hạn bởi nửa đường tròn, trục Ox và hai đường thẳng x = −1, x = 1. Tính thể tích khối tròn xoay tạo thành khi quay D quanh trục Ox.

s

Lời giải: