Giải SGK Toán 12 Kết nối tri thức Bài 13: Ứng dụng hình học của tích phân

1. Ứng dụng tích phân để tính diện tích hình phẳng

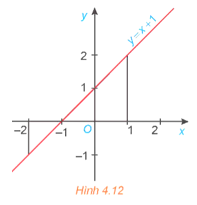
Hoạt động 1: Xét hình phẳng giới hạn bởi đường thẳng y = f(x) = x + 1, trục hoành và hai đường thẳng x = −2; x = 1 (H.4.12).

a) Tính diện tích S của hình phẳng này.

b) Tính $\underset{-2}{\overset{1}{\int }}\left|f\left(x\right)\right|dx$ và so sánh với S.

Lời giải:

a) Xác định các điểm như hình dưới:

Ta có: 

Khi đó: 

Hay 

b) Ta có:

Vậy .

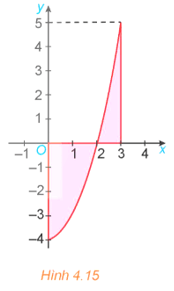
Luyện tập 1: Tính diện tích hình phẳng giới hạn bởi parabol y = x2 – 4, trục hoành và hai đường thẳng x = 0; x = 3 (H.4.15).

Lời giải:

Diện tích hình phẳng cần tính là:

$\underset{0}{\overset{3}{\int }}\left|x^2-4\right|dx$$=\underset{0}{\overset{2}{\int }}\left|x^2-4\right|dx+\underset{2}{\overset{3}{\int }}\left|x^2-4\right|dx$$=\underset{0}{\overset{2}{\int }}\left(4-x^2\right)dx+\underset{2}{\overset{3}{\int }}\left(x^2-4\right)dx$

$={\left(4x-\frac{x^3}{3}\right)|}_0^2+{\left(\frac{x^3}{3}-4x\right)|}_2^3$$=\frac{16}{3}-3+\frac{16}{3}=\frac{23}{3}$

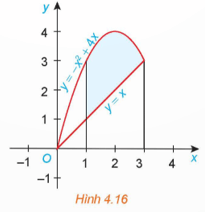
Hoạt động 2: Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của các hàm số f(x) = −x2 + 4x, g(x) = x và hai đường thẳng x = 1, x = 3 (H.4.16).

a) Giả sử S1 là diện tích hình phẳng giới hạn bởi parabol y = −x2 + 4x, trục hoành và hai đường thẳng x = 1, x = 3; S2 là diện tích hình phẳng giới hạn bởi đường thẳng y = x, trục hoành và hai đường thẳng x = 1, x = 3. Tính S1, S2 và từ đó suy ra S.

b) Tính $\underset{1}{\overset{3}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx$ và so sánh với S.

Lời giải:

Luyện tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số $y=\sqrt{x}$, y = x – 2 và hai đường thẳng x = 1, x = 4.

Lời giải:

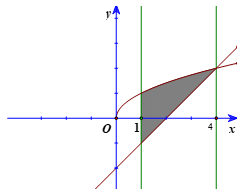
Diện tích hình phẳng cần tính là:

$S=\underset{1}{\overset{4}{\int }}\left|\sqrt{x}-x+2\right|dx$$=\underset{1}{\overset{4}{\int }}\left(\sqrt{x}-x+2\right)dx$$={\left.\left(\frac{2}{3}{x}^{\frac{3}{2}}-\frac{x^2}{2}+2x\right)\right|}_1^4$$=\frac{16}{3}-\frac{13}{6}=\frac{19}{6}$

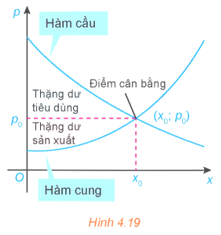
Vận dụng 1: Ta biết rằng hàm cầu liên quan đến giá p của một sản phẩm với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm với mức độ sẵn sàng cung cấp sản phẩm của nhà sản xuất. Điểm cắt nhau (x0; p0) của đồ thị hàm cầu p = D(x) và đồ thị hàm cung p = S(x) được gọi là điểm cân bằng.

Các nhà kinh tế gọi diện tích của hình giới hạn bởi đồ thị hàm cầu, đường ngang p = p0 và đường thẳng đứng x = 0 là thặng dư tiêu dùng. Tương tự, diện tích của hình giới hạn bởi đồ thị của hàm cung, đường nằm ngang p = p0 và đường thẳng đứng x = 0 được gọi là thặng dư sản xuất, như trong Hình 4.19.

(Theo R.Larson, Brief Calculus: An Applied Approach, 8th edition, Cengage Learning, 2009).

Giả sử hàm cung và hàm cầu của một loại sản phẩm được mô hình hóa bởi:

Hàm cầu: p = −0,36x + 9 và hàm cung: p = 0,14x + 2, trong đó x là số đơn vị sản phẩm. Tìm thặng dư tiêu dùng và thặng dư sản xuất cho sản phẩm này.

Lời giải:

Gọi điểm  là điểm cân bằng

Khi đó:  

Giá trị thặng dư tiêu dùng là diện tích hình phẳng giới hạn bởi hàm cầu , hàm số  và hai đường thẳng :

Giá trị thặng dư sản xuất là diện tích hình phẳng giới hạn bởi hàm cung: , hàm số  và hai đường thẳng :

2. Ứng dụng tích phân để tính thể tích vật thể

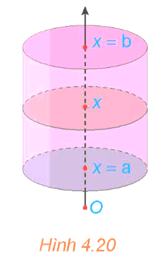
Hoạt động 3: Xét hình trụ có bán kính đáy R, có trục là trục hoành Ox, nằm giữa hai mặt phẳng x = a và x = b (a < b) (H.4.20).

a) Tính thể tích V của hình trụ.

b) Tính diện tích mặt cắt S(x) khi cắt hình trụ bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x (a ≤ x ≤ b). Từ đó tính $\underset{a}{\overset{b}{\int }}S\left(x\right)dx$ và so sánh với V.

Lời giải:

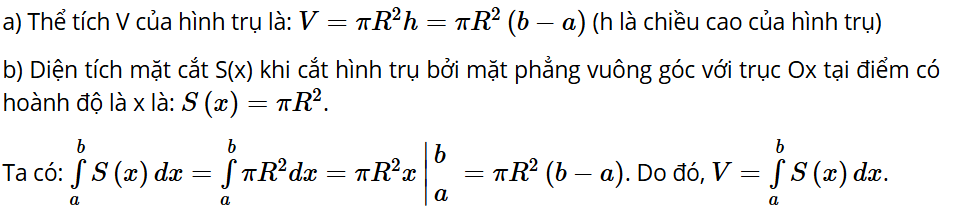
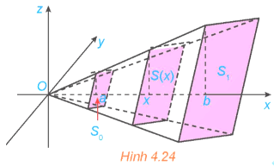
Vận dụng 2: Tính thể tích của khối chóp cụt đều có diện tích hai đáy là S0, S1 và chiều cao bằng h (H.4.24). Từ đó suy ra công thức tính thể tích khối chóp đều có diện tích đáy bằng S và chiều cao bằng h.

Lời giải:

Chọn hệ trục tọa độ Oxyz như hình vẽ.

Gọi a, b lần lượt là khoảng cách từ O đến đáy nhỏ và đáy lớn của hình chóp. Khi đó chiều cao của hình chóp cụt là h = b – a.

Thiết diện của khối chóp cụt khi cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x (a ≤ x ≤ b) là một đa giác đều đồng dạng với đáy lớn của hình chóp cụt theo tỉ số đồng dạng là $\frac{x}{b}$

Khi đó $\frac{S\left(x\right)}{S_1}=\frac{x^2}{b^2}\Rightarrow S\left(x\right)=\frac{x^2}{b^2}.S_1$

Do đó thể tích khối chóp cụt đều là:

$V=\underset{a}{\overset{b}{\int }}S\left(x\right)dx=\underset{a}{\overset{b}{\int }}\frac{x^2}{b^2}{S}_{1}dx={\frac{S_1}{b^2}.\frac{x^3}{3}|}_a^b$$=\frac{S_1}{3b^2}\left(b^3-a^3\right)$

$=\frac{b-a}{3b^2}.\left(S_1{b}^2+S_{1}ab+S_1{a}^2\right)$$=\frac{h}{3}.\left[S_1+S_1\frac{a}{b}+S_1{\left(\frac{a}{b}\right)}^2\right]$

Vì $\frac{S_0}{S_1}={\left(\frac{a}{b}\right)}^2\Rightarrow S_0=S_1.{\left(\frac{a}{b}\right)}^2$; $S_0{S}_1=S_1^2.{\left(\frac{a}{b}\right)}^2$$\Rightarrow \sqrt{S_0{S}_1}=S_1.\frac{a}{b}$

Do đó $V=\frac{h}{3}.\left[S_1+\sqrt{S_1.S_0}+S_0\right]$

Khối chóp đều được coi là khối chóp cụt đều khi S0 = 0.

Do đó thể tích khối chóp đều là $V=\frac{1}{3}.S.h$

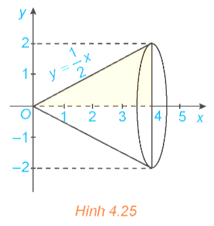
Hoạt động 4: Xét hình phẳng giới hạn bởi đồ thị hàm số $f\left(x\right)=\frac{1}{2}x$, trục hoành và hai đường thẳng x = 0, x = 4. Khi quay hình phẳng này xung quanh trục hoành Ox ta được khối nón có đỉnh là gốc O, trục là Ox và đáy là hình tròn bán kính bằng 2 (H.4.25).

a) Tính thể tích V của khối nón.

b) Chứng minh rằng khi cắt khối nón bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ bằng x (0 ≤ x ≤ 4) thì mặt cắt thu được là một hình tròn có bán kính là f(x), do đó diện tích mặt cắt là S(x) = πf2(x). Tính $\pi \underset{0}{\overset{4}{\int }}{f}^2\left(x\right)dx$ và so sánh với V.

Lời giải:

a) Khối nón có chiều cao bằng 4 và bán kính đáy bằng 2 nên có thể tích là:

b)

Gọi điểm  thuộc đồ thị hàm số 

Khi đó, bán kính của mặt cắt thu được bằng 

Do đó, diện tích mặt cắt là .

Ta có: 

Vậy  

Vận dụng 3:

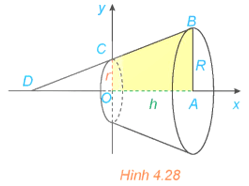
a) Tính thể tích của khối tròn xoay sinh ra khi quay hình thang vuông OABC trong mặt phẳng Oxy với OA = h, AB = R và OC = r, quanh trục Ox (H.4.28).

b) Từ công thức thu được ở phần a, hãy rút ra công thức tính thể tích của khối nón có bán kính đáy bằng R và chiều cao h.

Lời giải:

Bài tập

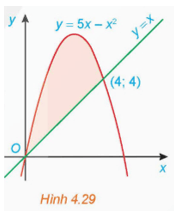
Bài 4.14: Tính diện tích của hình phẳng được tô màu trong Hình 4.29.

Lời giải:

Diện tích cần tính là:

$S=\underset{0}{\overset{4}{\int }}\left|5x-x^2-x\right|dx$$=\underset{0}{\overset{4}{\int }}\left|4x-x^2\right|dx$

$=\underset{0}{\overset{4}{\int }}\left(4x-x^2\right)dx$$={\left(2x^2-\frac{x^3}{3}\right)|}_0^4$$=\frac{32}{3}$

Bài 4.15: Tính diện tích của hình phẳng giới hạn bởi các đường:

a) y = ex, y = x2 – 1, x = −1, x = 1;

b) y = sinx, y = x, $x=\frac{\pi }{2},x=\pi$;

c) y = 9 – x2, y = 2x2, $x=-\sqrt{3},x=\sqrt{3}$;

d) $y=\sqrt{x},$ y = x2, x = 0, x = 1.

Lời giải:

a) Diện tích hình phẳng cần tìm là:

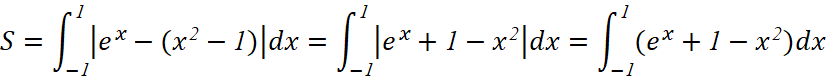
b) Diện tích hình phẳng cần tìm là:

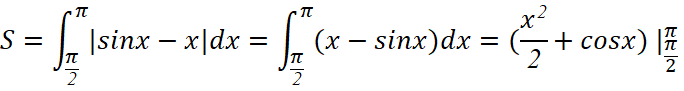
c) Diện tích hình phẳng cần tìm là:

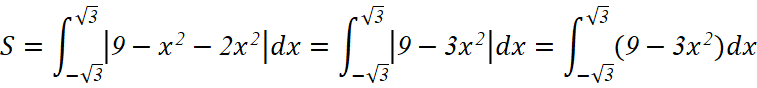
d) Diện tích hình phẳng cần tìm là:

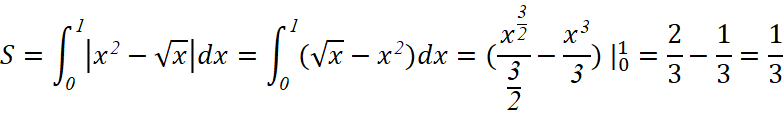
Bài 4.16: Các nhà kinh tế sử dụng đường cong Lorenz để minh họa sự phân phối thu nhập trong một quốc gia. Gọi x là đại diện cho phần trăm số gia đình trong một quốc gia và y là phần trăm tổng thu nhập, mô hình y = x sẽ đại diện cho một quốc gia mà các gia đình có thu nhập như nhau. Đường cong Lorenz y = f(x), biểu thị phân phối thu nhập thực tế. Diện tích giữa hai mô hình này, với 0 ≤ x ≤ 100, biểu thị “sự bất bình đẳng về thu nhập” của một quốc gia. Năm 2005, đường con Lorenz của Hoa Kỳ có thể được mô hình hóa bởi hàm số

y = (0,00061x2 + 0,0218x + 1723)2, 0 ≤ x ≤ 100,

trong đó x được tính từ các gia đình nghèo nhất đến giàu có nhất (Theo R.Larson, Brief Calculus: An Applied Approach, 8th edition, Cengage Learning, 2009).

Tìm sự bất bình đẳng thu nhập của Hoa Kỳ vào năm 2005.

Lời giải:

Bài 4.17: Tính thể tích của khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường sau xung quanh trục Ox: y = 2x – x2, y = 0, x = 0, x = 2.

Lời giải:

Thể tích cần tìm là:

$V=\pi \underset{0}{\overset{2}{\int }}{\left(2x-x^2\right)}^{2}dx$$=\pi \underset{0}{\overset{2}{\int }}\left(4x^2-4x^3+x^4\right)dx$$=\pi {\left(\frac{4}{3}{x}^3-x^4+\frac{x^5}{5}\right)|}_0^2$$=\frac{16\pi }{15}$

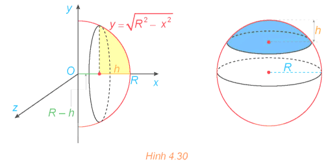
Bài 4.18: Khối chỏm cầu có bán kính R và chiều cao h (0 < h ≤ R) sinh ra khi quay hình phẳng giới hạn bởi cung tròn có phương trình $y=\sqrt{R^2-x^2}$, trục hoành và hai đường thẳng x = R – h, x = R xung quanh trục Ox (H.4.30). Tính thể tích của khối chỏm cầu này.

Lời giải:

Thể tích của khối chỏm cầu này là:

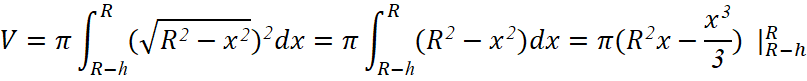
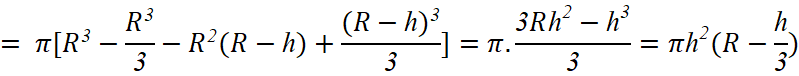
Bài 4.19: Cho tam giác vuông OAB có cạnh OA = a nằm trên trục Ox và ${\mathrm{AOB^\backslash widehat\{AOB\}AOB}}^{}=\alpha \left(0<\alpha \le \frac{\pi }{4}\right)$. Gọi β là khối tròn xoay sinh ra khi quay miền tam giác OAB xung quanh trục Ox (H.4.31).

a) Tính thể tích V của β theo a và α.

b) Tìm α sao cho thể tích V lớn nhất

Lời giải: