Giải SGK Toán 12 Kết nối tri thức Bài 7: Hệ trục tọa độ trong không gian - Giải SGK Toán 12 - Kết nối tri thức

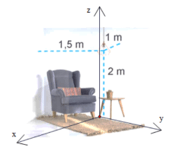
Mở đầu: Trong Hình 2.34, một chiếc bóng đèn được treo cách sàn nhà là 2 m, cách hai bức tường lần lượt là 1 m và 1,5 m. Kiến thức toán học nào giúp mô tả chính xác và ngắn gọn vị trí của chiếc bóng đèn trong không gian?

Mở đầu trang 60 Toán 12 Kết nối tri thức Tập 1 | Giải Toán 12

Trả lời:

- Để mô tả chính xác và ngắn gọn vị trí của chiếc bóng đèn trong không gian, chúng ta có thể sử dụng hệ tọa độ Oxyz trong không gian và khoảng cách các điểm trong không gian.

1. Hệ trục tọa độ trong không gian

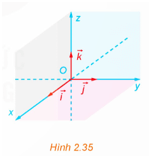
Hoạt động 1: Trong không gian, xét ba trục Ox, Oy, Oz có chung gốc O và đôi một vuông góc với nhau. Gọi $\vec{i}, \vec{j}, \vec{k}$ là các vectơ đơn vị trên các trục đó (H.2.35).

a) Gọi tên các mặt phẳng tọa độ có trong Hình 2.35.

b) Các mặt phẳng tọa độ trong Hình 2.35 có đôi một vuông góc với nhau?

HĐ1 trang 60 Toán 12 Kết nối tri thức Tập 1 | Giải Toán 12

Trả lời:

a) Các mặt phẳng tọa độ là (Oxy), (Oxz), (Oyz).

b) Vì Ox ⊥ Oy, Ox ⊥ Oz nên Ox ⊥ (Oyz) => (Oxy) ⊥ (Oyz); (Oxz) ⊥ (Oyz).

Tương tự (Oxy) ⊥ (Oxz).

Do đó các mặt phẳng này đôi một vuông góc với nhau.

Câu hỏi: Góc căn phòng trong Hình 2.34 có gợi lên hình ảnh về hệ tọa độ Oxyz trong không gian hay không? Nếu có, hãy mô tả gốc tọa độ và các mặt phẳng tọa độ trong hình ảnh đó.

Trả lời:

Góc căn phòng trong Hình 2.34 gợi lên hình ảnh về hệ tọa độ Oxyz trong không gian.

Câu hỏi trang 61 Toán 12 Kết nối tri thức Tập 1 | Giải Toán 12

Mô tả: Hệ tọa độ Oxyz có:

+) Mặt phẳng (Oxy) là sàn nhà, hai mặt phẳng (Oyz), (Oxz) là hai bức tường. Khi đó ba mặt phẳng đôi một vuông góc với nhau.

+) Gốc tọa độ O trùng với một góc phòng là giao điểm của 3 trục Ox, Oy, Oz.

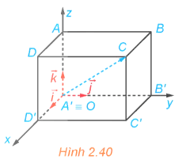
Luyện tập 1: Cho hình hộp chữ nhật ABCD.A'B'C'D'. Có thể lập một hệ tọa độ Oxyz có gốc O trùng với đỉnh C và các vectơ $\vec{i}, \vec{j}, \vec{k}$ lần lượt cùng hướng với các vectơ $\vec{C B}, \vec{C D}, \vec{C C^{'}}$ không? Giải thích vì sao.

Trả lời:

Vì là hình hộp chữ nhật nên các cạnh và đôi một vuông góc với nhau. Các vectơ cùng có điểm đầu là .

Do đó, suy ra có thể lập một hệ tọa độ có gốc trùng với đỉnh và các vectơ lần lượt cùng hướng với các vectơ .

2. Tọa độ của điểm, tọa độ của vectơ trong không gian

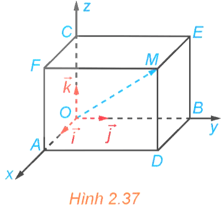
Hoạt động 2: Trong không gian Oxyz, cho một điểm M không thuộc các mặt phẳng tọa độ. Vẽ hình hộp chữ nhật OADB.CFME có ba đỉnh A, B, C lần lượt thuộc các tia Ox, Oy, Oz (H.2.37).

a) Hai vectơ $\vec{O M}$ và $\vec{O A} + \vec{O B} + \vec{O C}$ có bằng nhau không?

b) Giải thích vì sao có thể viết $\vec{O M} = x \vec{i} + y \vec{j} + z \vec{k}$ với x, y, z là các số thực.

Trả lời:

HĐ2 trang 61 Toán 12 Kết nối tri thức Tập 1 | Giải Toán 12

a) Vì OADB.CFME là hình hộp chữ nhật nên theo quy tắc hình hộp ta có:

$\vec{O A} + \vec{O B} + \vec{O C} = \vec{O M}$ .

b) Vì $\vec{i}$ là vectơ đơn vị trên trục Ox nên ta có $\vec{O A} = x \vec{i}$ với x là số thực.

Vì $\vec{j}$ là vectơ đơn vị trên trục Oy nên ta có $\vec{O B} = y \vec{j}$ với y là số thực.

Vì $\vec{k}$ là vectơ đơn vị trên trục Oz nên ta có $\vec{O C} = z \vec{k}$ với z là số thực.

Do đó $\vec{O M} = x \vec{i} + y \vec{j} + z \vec{k}$ với x, y, z là các số thực.

Câu hỏi: Hãy tìm tọa độ của gốc O.

Trả lời:

Vì $\vec{O O} = \vec{0} = 0 \vec{i} + 0 \vec{j} + 0 \vec{k}$ nên tọa độ của gốc O là (0; 0; 0).

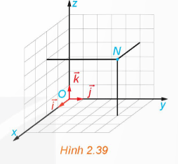
Luyện tập 2: Tìm tọa độ của điểm N trong Hình 2.39.

Luyện tập 2 trang 62 Toán 12 Kết nối tri thức Tập 1 | Giải Toán 12

Trả lời:

Ta có: . Do đó, .

Luyện tập 3: Trong Ví dụ 3, hãy xác định tọa độ của các điểm B, D và C'.

Luyện tập 3 trang 62 Toán 12 Kết nối tri thức Tập 1 | Giải Toán 12

Trả lời:

Theo ví dụ 3, ta có: m = 2, n = 3, p = 5.

Theo quy tắc hình bình hành ta có: $\vec{O B} = \vec{O B^{'}} + \vec{O A} = 3 \vec{j} + 5 \vec{k}$ .

Do đó B(0; 3; 5).

Theo quy tắc hình bình hành ta có: $\vec{O D} = \vec{O D^{'}} + \vec{O A} = 2 \vec{i} + 5 \vec{k}$ .

Do đó D(2; 0; 5).

Theo quy tắc hình bình hành ta có: $\vec{O C^{'}} = \vec{O D^{'}} + \vec{O B^{'}} = 2 \vec{i} + 3 \vec{j}$ .

Do đó C'(2; 3; 0).

Vận dụng 1: Trong tình huống mở đầu, hãy chọn một hệ tọa độ phù hợp và xác định tọa độ của chiếc bóng đèn đối với hệ tọa độ đó.

Trả lời:

- Mô tả: Hệ tọa độ có:

+ Mặt phẳng là sàn nhà, hai mặt phẳng hai bức tường. Khi đó, ba mặt phẳng đôi một vuông góc với nhau.

+ Gốc tọa độ (trùng với một góc phòng) là giao điểm của ba trục .

=> Khi đó, bóng đèn có tọa độ .

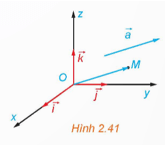
Hoạt động 3: Trong không gian Oxyz, cho vectơ $\vec{a}$ tùy ý (H.2.41). Lấy điểm M sao cho $\vec{O M} = \vec{a}$ và giải thích vì sao có bộ ba số (x; y; z) sao cho $\vec{a} = x \vec{i} + y \vec{j} + z \vec{k}$ .

HĐ3 trang 62 Toán 12 Kết nối tri thức Tập 1 | Giải Toán 12

Trả lời:

Theo khái niệm về tọa độ của điểm trong không gian, ta có:

$\vec{O M} = x \vec{i} + y \vec{j} + z \vec{k}$ .

Mà $\vec{O M} = \vec{a}$ nên $\vec{a} = x \vec{i} + y \vec{j} + z \vec{k}$ .

Do đó có bộ ba số (x; y; z) sao cho $\vec{a} = x \vec{i} + y \vec{j} + z \vec{k}$ .

Luyện tập 4: Trong không gian Oxyz, hãy xác định tọa độ của vectơ $\vec{i} + 2 \vec{j} + 5 \vec{k}$ .

Trả lời:

- Tọa độ của vectơ $\vec{i} + 2 \vec{j} + 5 \vec{k}$ là (1; 2; 5).

Hoạt động 4: Trong không gian Oxyz, cho hai điểm M(x; y; z) và N(x'; y'; z').

a) Hãy biểu diễn hai vectơ $\vec{O M}$ và $\vec{O N}$ qua các vectơ $\vec{i}, \vec{j}$ và $\vec{k}$ .

b) Xác định tọa độ của vectơ $\vec{M N}$ .

Trả lời:

a) Có $\vec{O M} = x \vec{i} + y \vec{j} + z \vec{k}$ ; $\vec{O N} = x^{'} \vec{i} + y^{'} \vec{j} + z^{'} \vec{k}$ .

b) Có

$\vec{M N} = \vec{O N} - \vec{O M} = (x^{'} \vec{i} + y^{'} \vec{j} + z^{'} \vec{k}) - (x \vec{i} + y \vec{j} + z \vec{k}) = (x^{'} - x) \vec{i} + (y^{'} - y) \vec{j} + (z^{'} - z) \vec{k}$ .

Do đó $\vec{M N} = (x^{'} - x; y^{'} - y; z^{'} - z)$ .

Luyện tập 5: Trong Ví dụ 5, xác định tọa độ của các điểm D và D' sao cho ABCD.A'B'C'D' là hình hộp.

Trả lời:

Gọi tọa độ của điểm là , tọa độ của điểm là , khi đó và .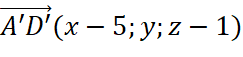

Để là hình hộp là hình bình hành.

Do đó, => 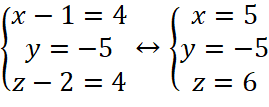. Suy ra .

Để là hình hộp là hình bình hành.

Do đó, => 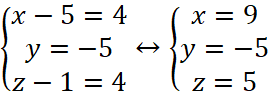. Suy ra .

Vận dụng 2: Để theo dõi hành trình của một chiếc máy bay, ta có thể lập hệ tọa độ Oxyz có gốc O trùng với vị trí của trung tâm kiểm soát không lưu, mặt phẳng (Oxy) trùng với mặt đất (được coi là phẳng) với trục Ox hướng về phía tây, trục Oy hướng về phía nam và trục Oz hướng thẳng đứng lên trời (H.2.43). Sau khi cất cánh và đạt độ cao nhất định, chiếc máy bay duy trì hướng bay về phía nam với tốc độ không đổi là 890 km/h trong nửa giờ. Xác định tọa độ của vectơ biểu diễn độ dịch chuyển của chiếc máy bay trong nửa giờ đó đối với hệ tọa độ đã chọn, biết rằng đơn vị đo trong không gian Oxyz được lấy theo kilômét.

Vận dụng 2 trang 64 Toán 12 Kết nối tri thức Tập 1 | Giải Toán 12

Trả lời:

Bài tập

Bài 2.13: Trong không gian Oxyz, cho ba vectơ $\vec{a}, \vec{b}, \vec{c}$ đều khác $\vec{0}$ và có giá đôi một vuông góc. Những mệnh đề nào sau đây là đúng?

a) Có thể lập một hệ tọa độ Oxyz có các trục tọa độ lần lượt song song với giá của các vectơ $\vec{a}, \vec{b}, \vec{c}$ .

b) Có thể lập một hệ tọa độ Oxyz có các trục tọa độ lần lượt trùng với giá của các vectơ $\vec{a}, \vec{b}, \vec{c}$ .

c) Có thể lập một hệ tọa độ Oxyz có các vectơ $\vec{i}, \vec{j}, \vec{k}$ lần lượt bằng các vectơ $\vec{a}, \vec{b}, \vec{c}$ .

d) Có thể lập một hệ tọa độ Oxyz có các vectơ $\vec{i}, \vec{j}, \vec{k}$ lần lượt cùng phương với các vectơ $\vec{a}, \vec{b}, \vec{c}$ .

Trả lời:

Các mệnh đề đúng là a) và d).

Bài 2.14: Hãy mô tả hệ tọa độ Oxyz trong căn phòng ở Hình 2.44 sao cho gốc O trùng với góc trên của căn phòng, khung tranh nằm trong mặt phẳng (Oxy) và mặt trần nhà trùng với mặt phẳng (Oxz).

Bài 2.14 trang 64 Toán 12 Kết nối tri thức Tập 1 | Giải Toán 12

Trả lời:

Bài 2.15: Trong không gian Oxyz, xác định tọa độ của vectơ $\vec{A B}$ trong mỗi trường hợp sau:

a) A(0; 0; 0) và B(4; 2; −5);

b) A(1; −3; 7) và B(1; −3; 7);

c) A(5; 4; 9) và B(−5; 7; 2).

Trả lời:

a) $\vec{A B} = (4; 2; - 5)$ .

b) $\vec{A B} = (0; 0; 0)$ .

c) $\vec{A B} = (- 10; 3; - 7)$ .

Bài 2.16: Trong không gian Oxyz, xác định tọa độ của điểm A trong mỗi trường hợp sau:

a) A trùng với gốc tọa độ;

b) A nằm trên tia Ox và OA = 2.

c) A nằm trên tia đối của tia Oy và OA = 3.

Trả lời:

a. trùng với gốc tọa độ nên .

b. Vì nằm trên tia và nên . Do đó,

c. Vì nằm trên tia đối của tia và nên 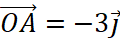. Do đó, .

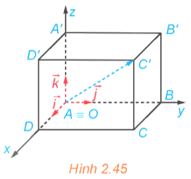
Bài 2.17: Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A'B'C'D' có đỉnh A trùng với gốc O và các đỉnh D, B, A' có tọa độ lần lượt là (2; 0; 0), (0; 4; 0), (0; 0; 3) (H.2.45). Xác định tọa độ của các đỉnh còn lại của hình hộp chữ nhật.

Bài 2.17 trang 65 Toán 12 Kết nối tri thức Tập 1 | Giải Toán 12

Trả lời:

Đỉnh A trùng với gốc tọa độ nên A(0; 0; 0).

Ta có D(2; 0; 0) nên $\vec{O D} = 2 \vec{i}$ ; B(0; 4; 0) nên $\vec{O B} = 4 \vec{j}$ ; A'(0; 0; 3) nên $\vec{O A^{'}} = 3 \vec{k}$ .

Theo quy tắc hình hộp, ta có: $\vec{O C^{'}} = \vec{O D} + \vec{O B} + \vec{O A^{'}} = 2 \vec{i} + 4 \vec{j} + 3 \vec{k}$ .

Do đó C'(2; 4; 3).

Theo quy tắc hình bình hành, ta có: $\vec{O C} = \vec{O D} + \vec{O B} = 2 \vec{i} + 4 \vec{j}$ .

Do đó C(2; 4; 0).

Theo quy tắc hình bình hành, ta có: $\vec{O D^{'}} = \vec{O D} + \vec{O A^{'}} = 2 \vec{i} + 3 \vec{k}$ .

Do đó D'(2; 0; 3).

Theo quy tắc hình bình hành, ta có: $\vec{O B^{'}} = \vec{O B} + \vec{O A^{'}} = 4 \vec{j} + 3 \vec{k}$ .

Do đó B'(0; 4; 3).

Bài 2.18: Trong không gian Oxyz, cho hình hộp OABC.O'A'B'C' có A(1; 1; −1), B(0; 3; 0), C'(2; −3; 6).

a) Xác định tọa độ của điểm C.

b) Xác định tọa độ các đỉnh còn lại của hình hộp.

Trả lời:

a) Ta có:

Vì là hình hộp nên là hình bình hành.

Do đó:

b) Vì là hình hộp nên:

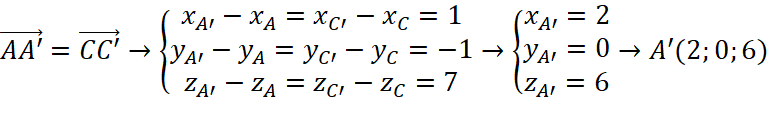
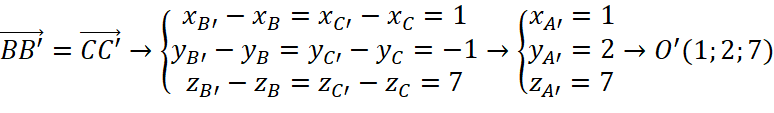
Bài 2.19: Trong Vận dụng 2, hãy giải thích vì sao tại mỗi thời điểm chiếc máy bay di chuyển trên đường băng thì tọa độ của nó luôn có dạng (x; y; 0) với x, y là hai số thực nào đó.

Trả lời:

- Khi máy bay di chuyển trên đường băng tức là máy bay di chuyển ở trên mặt đất,tức là thuộc mặt phẳng (Oxy). Do đó máy bay khi di chuyển trên đường băng thì tọa độ của nó luôn có dạng (x; y; 0) với x, y là hai số thực nào đó.