Giải SGK Toán 12 Kết nối tri thức Bài 18: Xác suất có điều kiện

Mở đầu: Ô cửa bí mật (Let’s Make a Deal) là một trò chơi trên truyền hình nổi tiếng ở Mỹ, đã được mua bản quyền và phát sóng ở nhiều nước trên thế giới. Nội dung trò chơi như sau:

- Người chơi được mời lên sân khấu và đứng trước ba cánh cửa đóng kín. Sau một cánh cửa có chiếc ô tô, sau mỗi cánh cửa còn lại là một con lừa. Người chưa được yêu cầu chọn ngẫu nhiên một cánh cửa, nhưng không được mở ra.

- Tiếp đó người quản trò tuyên bố sẽ mở ngẫu nhiên một trong hai cánh cửa người chơi không chọn mà sau cửa đó là con lừa. Người quản trò hỏi người chơi muốn giữ nguyên sự lựa chọn ban đầu của mình hay muốn chuyển sang cửa chưa mở còn lại.

Các kiến thức trong bài học này sẽ giúp cho người chơi lời khuyên.

Lời giải:

+ Trước khi người quản trò mở ô cửa số 3 thì xác suất để ô cửa số 1 hay ô cửa số 2 có ô tô là như nhau (bằng $\frac{1}{3}$).

+ Nếu như quản trò mở ô cửa số 3 – ô cửa có con lừa thì lúc này xác suất có ô tô ở cửa số 1 và cửa số 2 không còn bằng nhau nữa.

1. Xác suất có điều kiện

Hoạt động 1: Hình thành khái niệm xác suất có điều kiện

Trong một hộp kín có 7 chiếc bút bi xanh và 5 chiếc bút bi đen, các chiếc bút có cùng kích thước và khối lượng. Bạn Sơn lấy ngẫu nhiên một chiếc bút bi trong hộp, không trả lại. Sau đó Tùng lấy ngẫu nhiên một trong 11 chiếc bút còn lại. Tính xác suất để Tùng lấy được bút bi xanh nếu biết rằng Sơn đã lấy được bút bi đen.

Lời giải:

Luyện tập 1: Trở lại Ví dụ 1. Tính $P\left(A|\overline{B}\right)$ bằng định nghĩa và bằng công thức.

Lời giải:

A: ”An lấy được viên bi trắng”

B: ”Bình lấy được viên bi trắng”

: ”Bình lấy được viên bi đen”

Cách 1: Bằng định nghĩa

Nếu xảy ra tức là Bình lấy được viên bi đen. Khi đó, trong hộp còn lại 29 viên bi với 20 viên bi trắng và 9 viên bi đen. 

Vậy 

Cách 2: Bằng công thức

Bình có 30 cách chọn, An có 29 cách chọn một viên bi trong hộp

Do đó 

Bình có 10 cách chọn một viên bi đen, An có 29 cách chọn từ 29 viên bi còn lại

Do đó  và  

Bình có 10 cách chọn một viên bi đen, An có 20 cách chọn một viên bi trắng

Do đó  và  

Vậy 

Luyện tập 2: Chứng tỏ rằng nếu A và B là hai biến cố độc lập thì: $P\left(\overline{A}|B\right)=P\left(\overline{A}\right)$ và $P\left(A|\overline{B}\right)=P\left(A\right)$

Lời giải:

Vì A và B là hai biến cố độc lập nên các cặp biến cố $\overline{A}$ và B; A và $\overline{B}$ cũng độc lập.

Theo định nghĩa $P\left(\overline{A}|B\right)$ là xác suất của $\overline{A}$ (tức là xác suất không xuất hiện của A) biết rằng biến cố B đã xảy ra. Vì $\overline{A}$ , B độc lập nên việc xảy ra B không ảnh hưởng tới xác suất không xuất hiện của A.

Do đó $P\left(\overline{A}|B\right)=P\left(\overline{A}\right)$.

Tương tự $P\left(A|\overline{B}\right)$ là xác suất của A biết rằng biến cố B không xảy ra. Vì A, $\overline{B}$độc lập nên việc không xảy ra B không ảnh hưởng tới xác suất xuất hiện của A. 

Luyện tập 3: Một công ty dược phẩm muốn so sánh tác dụng điều trị bệnh X của hai loại thuốc M và N. Công ty đã tiến hành thử nghiệm với 4 000 bệnh nhân mắc bệnh X trong đó 2 400 bệnh nhân dùng thuốc M, 1600 bệnh nhân còn lại dùng thuốc N. Kết quả được cho trong bảng dữ liệu thống kê 2 × 2 như sau:

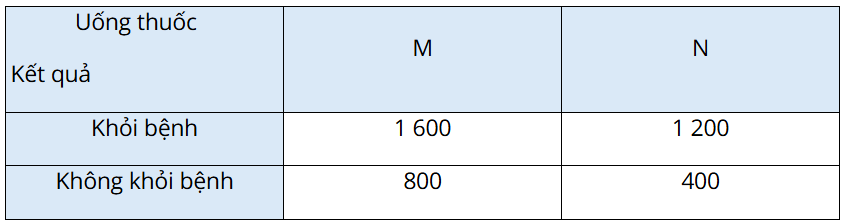
Chọn ngẫu nhiên một bệnh nhân trong số 4 000 bệnh nhân thử nghiệm sau khi uống thuốc. Tính xác suất để bệnh nhân đó

a) Uống thuốc M, biết rằng bệnh nhân đó khỏi bệnh;

b) Uống thuốc N, biết rằng bệnh nhân đó không khỏi bệnh.

Lời giải:

Không gian mẫu  là tập hợp gồm 4000 bệnh nhân mắc bệnh X ⇒ 

a) Gọi A là biến cố:”Người đó uống thuốc M”; B là biến cố:”Người đó khỏi bệnh”

Khi đó AB là biến cố:”Người đó uống thuốc M và khỏi bệnh”

Ta cần tính 

Số người khỏi bệnh là 1600 + 1200 = 2800 ⇒ 

Vậy  

Trong số những người khỏi bệnh, có 1600 người uống thuốc M ⇒ 

Vậy  

Do đó: 

b)  là biến cố:”Người đó uống thuốc N”

 là biến cố:”Người đó không qua khỏi”

Khi đó  là biến cố:”Người đó uống thuốc N và không khỏi bệnh”

Ta cần tính 

Số người không khỏi bệnh là 800 + 400 = 1200 ⇒ 

Vậy  

Trong số những người không khỏi bệnh, có 400 người uống thuốc M 

⇒ 

Vậy  

Do đó: 

2. Công thức nhân xác suất

Hoạt động 2: Hình thành công thức nhân xác suất

Chứng minh rằng, với hai biến cố A và B, P(B) > 0, ta có:

P(AB) = P(B) ∙ P(A | B).

Lời giải:

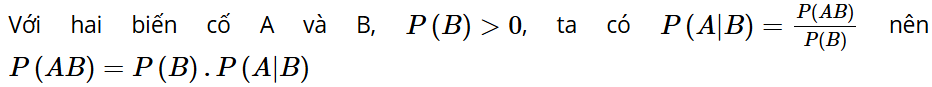
Luyện tập 4: Trở lại Ví dụ 4. Tính xác suất để:

a) Sơn lấy được bút bi xanh và Tùng lấy được bút bi đen;

b) Hai chiếc bút lấy ra có cùng màu.

Lời giải:

a) Gọi C là biến cố: “Bạn Sơn lấy được bút bi xanh”;

           D là biến cố: “Bạn Tùng lấy được bút bi đen”.

Ta cần tính P(CD).

Vì n(C) = 7 nên P(C) = $\frac{7}{12}$.

Nếu C xảy ra tức là bạn Sơn lấy được bút bi xanh thì trong hộp còn lại 11 bút bi với 6 bút bi xanh và 5 bút bi đen. Do đó, P(D | C) = $\frac{5}{11}$.

Theo công thức nhân xác suất: P(CD) = P(C) ∙ P(D | C) = $\frac{7}{12}\cdot \frac{5}{11}=\frac{35}{132}.$

b) Tương tự như câu a), ta tính được:

Xác suất để hai chiếc bút bi lấy ra có cùng màu đen là: P(ĐĐ) = $\frac{5}{12}\cdot \frac{4}{11}=\frac{20}{132}$;

Xác suất để hai chiếc bút bi lấy ra có cùng màu xanh là: P(XX) = $\frac{7}{12}\cdot \frac{6}{11}=\frac{42}{132}$.

Xác suất để hai chiếc bút bi lấy ra có cùng màu là: $\frac{20}{132}+\frac{42}{132}=\frac{62}{132}=\frac{31}{66}$

Vận dụng: Trở lại trò chơi “Ô cửa bí mật” trong tình huống mở đầu. Giả sử người chơi chọn cửa số 1 và người quản trò mở cửa số 3.

Kí hiệu E1; E2; E3 tương ứng là các biến cố: “Sau ô cửa số 1 có ô tô”; “Sau ô cửa số 2 có ô tô”; “Sau ô cửa số 3 có ô tô” và H là biến cố: “Người quản trò mở ô cửa số 3 thấy con lừa”.

Sau khi người quản trò mở cánh cửa số 3 thấy con lừa, tức là khi H xảy ra. Để quyết định thay đổi lựa chọn hay không, người chơi cần so sánh hai xác suất có điều kiện: P(E1 | H) và P(E2 | H).

a) Chứng minh rằng:

● P(E1) = P(E2) = P(E3) = $\frac{1}{3}$;

● P(H | E1) = $\frac{1}{2}$ và P(H | E2) = 1.

b) Sử dụng công thức tính xác suất có điều kiện và công thức nhân xác suất, chứng minh rằng:

● P(E1 | H) = $\frac{P\left(E_1\right)\cdot P\left(H|E_1\right)}{P\left(H\right)}$;

● P(E2 | H) = $\frac{P\left(E_2\right)\cdot P\left(H|E_2\right)}{P\left(H\right)}$.

c) Từ các kết quả trên hãy suy ra:

P(E2 | H) = 2P(E1 | H).

Từ đó hãy đưa ra lời khuyên cho người chơi: Nên giữ nguyên sự lựa chọn ban đầu hay chuyển sang cửa chưa mở còn lại?

Hướng dẫn: Nếu E1 xảy ra, tức là sau cửa số 1 có ô tô. Khi đó, sau cửa số 2 và 3 là con lừa. Người quản trò chọn ngẫu nhiên một trong hai cửa số 2 và 3 để mở ra. Do đó, việc chọn cửa số 2 hay cửa số 3 có khả năng như nhau. Vậy P(H | E1) = $\frac{1}{2}$.

Nếu E2 xảy ra, tức là sau cửa số 2 có ô tô. Khi đó, người quản trò chắc chắn phải mở cửa số 3. Do đó, P(H | E2) = 1.

Lời giải:

a) Vì chỉ có một chiếc ô tô ở đằng sau cả 3 cánh cửa nên:

Nếu  xảy ra, tức là sau cửa sổ 1 có ô tô. Khi đó, sau cửa số 2 và 3 là con lừa. Người quản trò chọn ngẫu nhiên một trong hai cửa số 2 và 3 để mở ra. Do đó, việc chọn cửa số 2 hay cửa số 3 có khả năng như nhau. Vậy 

Nếu  xảy ra, tức là cửa số 2 có ô tô. Khi đó, người quản trò chắc chắn phải mở cửa số 3. Do đó 

b) Theo công thức nhân xác suất: 

Tương tự: 

c) Từ kết quả của câu b), ta có: 

Từ kết quả của câu a), ta có: ;  và 

Vậy 

Lời khuyên cho người chơi là nên chuyển sang cửa chưa mở còn lại.

Bài tập

Bài 6.1: Một hộp kín đựng 20 tấm thẻ giống hệt nhau đánh số từ 1 đến 20. Một người rút ngẫu nhiên ra một tấm thẻ từ trong hộp. Người đó được thông báo rằng thẻ rút ra mang số chẵn. Tính xác suất để người đó rút được thẻ số 10.

Lời giải:

Bài 6.2: Cho P(A) = 0,2; P(B) = 0,51; P(B | A) = 0,8. Tính P(A | B).

Lời giải:

Áp dụng công thức nhân xác suất, ta có: P(AB) = P(A) ∙ P(B | A) = 0,2 ∙ 0,8 = 0,16.

Khi đó, ta có: $P\left(A|B\right)=\frac{P\left(AB\right)}{P\left(B\right)}=\frac{\mathrm{0,16}}{\mathrm{0,51}}\approx \mathrm{0,3137}$

Bài 6.3: Gieo hai con xúc xắc cân đối, đồng chất. Tính xác suất để:

a) Tổng số chấm xuất hiện trên hai con xúc xắc bằng 7 nếu biết rằng ít nhất có một con xúc xắc xuất hiện mặt 5 chấm;

b) Có ít nhất có một con xúc xắc xuất hiện mặt 5 chấm nếu biết rằng tổng số chấm xuất hiện trên hai con xúc xắc bằng 7.

Lời giải:

Gieo hai con xúc xắc cân đối, đồng chất nên số phần tử của không gian mẫu là:

Gọi A là biến cố: "Tổng số chấm xuất hiện trên hai con xúc xắc bằng 7”

B là biến cố: "Có ít nhất có một con xúc xắc xuất hiện mặt 5 chấm”

Khi đó AB là biến cố: "Tổng số chấm xuất hiện trên hai con xúc xắc bằng 7 và có ít nhất có một con xúc xắc xuất hiện mặt 5 chấm”

Các kết quả thuận lợi cho biến cố A là: (1;6), (2;5), (3;4), (4;3), (5;2), (6;1)

⇒ ⇒  

Các kết quả thuận lợi cho biến cố B là: (1;5), (2;5), (3;5), (4;5), (5;5), (6;5), (5;1), (5;2), (5;3), (5;4), (5;6)

⇒ ⇒  

Các kết quả thuận lợi cho biến cố AB là: (2;5), (5;2)

⇒ ⇒  

a) Ta cần tính 

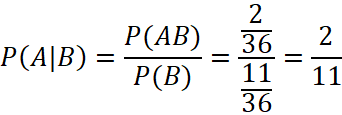
b) Ta cần tính 

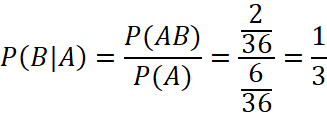
Bài 6.4: Gieo hai con xúc xắc cân đối, đồng chất. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc xắc đó không nhỏ hơn 10 nếu biết rằng có ít nhất một con xúc xắc xuất hiện mặt 5 chấm.

Lời giải:

Bài 6.5: Bạn An phải thực hiện hai thí nghiệm liên tiếp. Thí nghiệm thứ nhất có xác suất thành công là 0,7. Nếu thí nghiệm thứ nhất thành công thì xác suất thành công của thí nghiệm thứ hai là 0,9. Nếu thí nghiệm thứ nhất không thành công thì xác suất thành công của thí nghiệm thứ hai chỉ là 0,4. Tính xác suất để:

a) Cả hai thí nghiệm đều thành công;

b) Cả hai thí nghiệm đều không thành công;

c) Thí nghiệm thứ nhất thành công và thí nghiệm thứ hai không thành công.

Lời giải:

a) Gọi A là biến cố: “Thí nghiệm thứ nhất thành công” và B là biến cố: “Thí nghiệm thứ hai thành công”. Khi đó biến cố “Cả hai thí nghiệm đều thành công” là AB.

Theo công thức nhân xác suất ta có P(AB) = P(A) ∙ P(B | A).

Theo bài ra ta có P(A) = 0,7; P(B | A) = 0,9.

Thay vào ta được P(AB) = 0,7 ∙ 0,9 = 0,63.

b) Biến cố: “Cả hai thí nghiệm đều không thành công” là $\overline{A}\overline{B}$.

Theo công thức nhân xác suất ta có $P\left(\overline{A}\overline{B}\right)=P\left(\overline{A}\right)\cdot P\left(\overline{B}|\overline{A}\right)$.

Ta có $P\left(\overline{B}|\overline{A}\right)$ là xác suất để thí nghiệm thứ hai không thành công nếu thí nghiệm thứ nhất không thành công. Do đó, từ dữ kiện của bài toán ta có:

$P\left(\overline{B}|\overline{A}\right)=1–\mathrm{0,4}=\mathrm{0,6}$ ; $P\left(\overline{A}\right)=1–P\left(A\right)=1–\mathrm{0,7}=\mathrm{0,3}$.

Vậy $P\left(\overline{A}\overline{B}\right)=\mathrm{0,3}\cdot \mathrm{0,6}=\mathrm{0,18}$.

c) Biến cố “Thí nghiệm thứ nhất thành công và thí nghiệm thứ hai không thành công” là $P\left(A\overline{B}\right)=P\left(A\right)\cdot P\left(\overline{B}|A\right)$.

Theo công thức nhân xác suất ta có $P\left(A\overline{B}\right)=P\left(A\right)\cdot P\left(\overline{B}|A\right)$.

Ta có $P\left(\overline{B}|A\right)$ là xác suất để thí nghiệm thứ hai không thành công nếu thí nghiệm thứ nhất thành công. Do đó từ dữ kiện của bài toán ta có

 $P\left(\overline{B}|A\right)=1–\mathrm{0,9}=\mathrm{0,1};P\left(A\right)=\mathrm{0,7}$.

Vậy $P\left(\overline{B}|A\right)=\mathrm{0,7}\cdot \mathrm{0,1}=\mathrm{0,07}$

Bài 6.6: Trong một túi có một số chiếc kẹo cùng loại, chỉ khác màu, trong đó có 6 cái kẹo màu cam, còn lại là kẹo màu vàng. Hà lấy ngẫu nhiên một cái kẹo từ trong túi, không trả lại. Sau đó Hà lại lấy ngẫu nhiên thêm một cái kẹo khác từ trong túi. Biết rằng xác suất Hà lấy được cả hai cái kẹo màu cam là $\frac{1}{3}$. Hỏi ban đầu trong túi có bao nhiêu cái kẹo?

Lời giải:

Gọi A là biến cố:”Lấy được cái kẹo thứ nhất màu cam”

B là biến cố:”Lấy được cái kẹo thứ hai màu cam”

Khi đó AB là biến cố:”Lấy được cả hai cái kẹo màu cam”, 

Gọi số kẹo ban đầu có trong túi là n (n > 0)

Như vậy, trong túi có 6 cái kẹo màu cam và  cái kẹo màu vàng

Có n cách chọn cái kẹo thứ nhất và  cách chọn cái kẹo thứ hai

⇒ 

Sau khi Hà lấy được 1 cái kẹo màu cam thì còn lại  cái kẹo với 5 cái kẹo màu cam

⇒   và  

Ta có: 

Hay 

⇒ 

⇒ 

⇒  hoặc 

Vậy ban đầu trong túi có 10 cái kẹo