Giải SGK Toán 12 Kết nối tri thức Bài 14: Phương trình mặt phẳng

Mở đầu: Một vật thể chuyển động trong không gian Oxyz. Tại mỗi thời điểm t, vật thể ở vị trí M(cost – sint; cost + sint; cost). Hỏi vật thể có chuyển động trong một mặt phẳng cố định hay không?

Lời giải:

Sau khi học xong bài này, ta giải quyết bài toán này như sau:

Thời điểm t = 0, vật ở vị trí M1(1; 1; 1).

Thời điểm $t=\frac{\pi }{2}$ vật ở vị trí M2(−1; 1; 0).

Thời điểm t = π, vật ở vị trí M3(−1; −1; −1).

Có $\overrightarrow{M_1{M}_2}=\left(-2;0;-1\right)$ và $\overrightarrow{M_1{M}_3}=\left(-2;-2;-2\right)$ không cùng phương nên ba điểm M1, M2, M3 không thẳng hàng.

Mặt phẳng (M1M2M3) có $\overrightarrow{M_1{M}_2}=\left(-2;0;-1\right)$ và $\overrightarrow{M_1{M}_3}=\left(-2;-2;-2\right)$ là cặp vectơ chỉ phương nên có vectơ pháp tuyến

$\overrightarrow{n}=\left[\overrightarrow{M_1{M}_2},\overrightarrow{M_1{M}_3}\right]=\left(\left|\begin{array}{cc}0& -1\\ -2& -2\end{array}\right|;\left|\begin{array}{cc}-1& -2\\ -2& -2\end{array}\right|;\left|\begin{array}{cc}-2& 0\\ -2& -2\end{array}\right|\right)=\left(-2;-2;4\right)$

Mặt phẳng (M1M2M3) đi qua M1(1; 1; 1) và có vectơ pháp tuyến $\overrightarrow{n}=\left(-2;-2;4\right)$ có phương trình là: −2(x – 1) – 2(y – 1) + 4(z – 1) = 0 hay 2x + 2y – 4z = 0.

Ta có 2(cost – sint) + 2(cost + sint) – 4 cost = 0 nên vị trí M(cost – sint; cost + sint; cost) luôn thuộc mặt phẳng (M1M2M3).

Do đó vị trí M(cost – sint; cost + sint; cost) luôn thuộc mặt phẳng 2x + 2y – 4z = 0.

1. Vecto pháp tuyến và cặp vecto chỉ phương của mặt phẳng

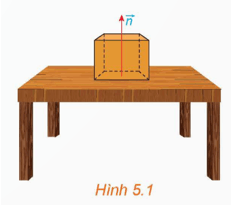
Hoạt động 1: Trên mặt bàn phẳng, đặt một vật. Khi đó, mặt bàn tác động lên vật phản lực pháp tuyến $\overrightarrow{n}$, giá của vectơ $\overrightarrow{n}$ vuông góc với mặt bàn. Nếu mặt bàn thuộc mặt phẳng nằm ngang thì $\overrightarrow{n}$ có phương gì? (H.5.1)

Lời giải:

- Giá của vectơ  vuông góc với mặt bàn nên nếu mặt bàn thuộc mặt phẳng nằm ngang thì giá của vectơ có phương thẳng đứng.

Luyện tập 1: Trong không gian Oxyz, cho các điểm A(1; −2; 3), B(−3; 0; 1). Gọi (α) là mặt phẳng trung trực của đoạn thẳng AB. Hãy chỉ ra một vectơ pháp tuyến của (α).

Lời giải:

Hoạt động 2: Trong không gian Oxyz, cho hai vectơ $\overrightarrow{u}=\left(a;b;c\right)$ và $\overrightarrow{v}=\left(a^{\prime };b^{\prime };c^{\prime }\right)$.

a) Vectơ $\overrightarrow{n}=\left(b{c}^{\prime }-b^{\prime }c;c{a}^{\prime }-c^{\prime }a;a{b}^{\prime }-a^{\prime }b\right)$ có vuông góc với cả hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ hay không?

b) $\overrightarrow{n}=\overrightarrow{0}$ khi và chỉ khi $\overrightarrow{u}$ và $\overrightarrow{v}$ có mối quan hệ gì?

Lời giải:

a) Ta có $\overrightarrow{n}.\overrightarrow{u}=\left(b{c}^{\prime }-b^{\prime }c\right).a+\left(c{a}^{\prime }-c^{\prime }a\right).b+\left(a{b}^{\prime }-a^{\prime }b\right).c$

= bc'a – b'ca + ca'b – c'ab + ab'c – a'bc

= (bc'a – c'ab) + (ab'c – b'ca) + (ca'b – a'bc)

= 0.

Do đó vectơ $\overrightarrow{n}$ vuông góc với vectơ $\overrightarrow{u}$.

Ta có $\overrightarrow{n}.\overrightarrow{v}=\left(b{c}^{\prime }-b^{\prime }c\right).a^{\prime }+\left(c{a}^{\prime }-c^{\prime }a\right).b^{\prime }+\left(a{b}^{\prime }-a^{\prime }b\right).c^{\prime }$

= bc'a' – b'ca' + ca'b' – c'ab' + ab'c' – a'bc'

= (bc'a' – c'a'b) + (ab'c' – b'c'a) + (ca'b' – a'b'c)

= 0.

Do đó vectơ $\overrightarrow{n}$ vuông góc với vectơ $\overrightarrow{v}$.

Suy ra vectơ $\overrightarrow{n}$ vuông góc với cả 2 vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$.

b) Nếu $\overrightarrow{n}=\overrightarrow{0}$ thì $\{\begin{array}{c}b{c}^{\prime }-b^{\prime }c=0\\ c{a}^{\prime }-c^{\prime }a=0\\ a{b}^{\prime }-a^{\prime }b=0\end{array}$ (I).

+) Nếu a = b = c = 0 thì (I) luôn đúng khi đó $\overrightarrow{u}$ và $\overrightarrow{v}$ cùng phương với nhau.

+) Nếu a ≠ 0; b ≠ 0; c ≠ 0 thì (I) ta suy ra $\{\begin{array}{c}\frac{b^{\prime }}{b}=\frac{c^{\prime }}{c}\\ \frac{a^{\prime }}{a}=\frac{c^{\prime }}{c}\\ \frac{a^{\prime }}{a}=\frac{b^{\prime }}{b}\end{array}$.

Do đó, a' = ka; b' = kb, c' = kc (k ∈ ℝ).

Suy ra $\overrightarrow{v}=k\overrightarrow{u}$. Do đó $\overrightarrow{u}$ và $\overrightarrow{v}$ cùng phương với nhau.

Vậy $\overrightarrow{n}=\overrightarrow{0}$ khi và chỉ khi $\overrightarrow{u}$ và $\overrightarrow{v}$ cùng phương.

Luyện tập 2: Trong không gian Oxyz, cho $\overrightarrow{u}=\left(2;3;1\right)$ và $\overrightarrow{v}=\left(4;6;2\right)$. Tính $\left[\overrightarrow{u},\overrightarrow{v}\right]$

Lời giải:

Ta có: .

Hoạt động 3: Trong không gian Oxyz, cho hai vectơ $\overrightarrow{u},\overrightarrow{v}$ không cùng phương và có giá nằm trong hoặc song song với mặt phẳng (P).

a) Vectơ $\left[\overrightarrow{u},\overrightarrow{v}\right]$ có khác vectơ-không và giá của nó có vuông góc với cả hai giá của $\overrightarrow{u},\overrightarrow{v}$ hay không?

b) Mặt phẳng (P) có nhận $\left[\overrightarrow{u},\overrightarrow{v}\right]$ làm một vectơ pháp tuyến hay không?

Lời giải:

Luyện tập 3: Trong không gian Oxyz, cho ba điểm không thẳng hàng A(1; −2; 1), B(−2; 1; 0), C(−2; 3; 2). Hãy chỉ ra một vectơ pháp tuyến của mặt phẳng (ABC).

Lời giải:

Ta có $\overrightarrow{AB}=\left(-3;3;-1\right)$ và $\overrightarrow{AC}=\left(-3;5;1\right)$ là các vectơ chỉ phương của mặt phẳng (ABC) nên mặt phẳng (ABC) nhận vectơ $\left[\overrightarrow{AB},\overrightarrow{AC}\right]$ làm vectơ pháp tuyến.

Ta có $\left[\overrightarrow{AB},\overrightarrow{AC}\right]=\left(\left|\begin{array}{cc}3& -1\\ 5& 1\end{array}\right|;\left|\begin{array}{cc}-1& -3\\ 1& -3\end{array}\right|;\left|\begin{array}{cc}-3& 3\\ -3& 5\end{array}\right|\right)=\left(8;6;-6\right)$

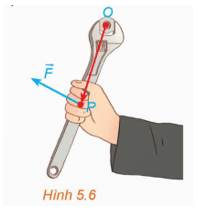
Vận dụng 1: Moment lực là một đại lượng Vật lí, thể hiện tác động gây ra sự quay quanh một điểm hoặc một trục của một vật thể. Trong không gian Oxyz, với đơn vị đo là mét, nếu tác động vào cán mỏ lết tại vị trí P một lực $\overrightarrow{F}$ để vặn con ốc ở vị trí O (H.5.6) thì moment lực $\overrightarrow{M}$ được tính bởi công thức $\overrightarrow{M}=\left[\overrightarrow{OP},\overrightarrow{F}\right]$

a) Cho $\overrightarrow{OP}=\left(x;y;z\right),\overrightarrow{F}=\left(a;b;c\right)$. Tính $\overrightarrow{M}$.

b) Giải thích vì sao, nếu giữ nguyên lực tác động $\overrightarrow{F}$ trong khi thay vị trí đặt lực từ P sang P' sao cho $\overrightarrow{O{P}^{\prime }}=2\overrightarrow{OP}$ thì moment lực sẽ tăng lên gấp đôi. Từ đó, ta có thể rút ra điều gì để đỡ tốn sức khi dùng mỏ lết vặn ốc?

Lời giải:

a) .

b) Ta có: .

Như vậy, khi giữ nguyên lực tác động  trong khi thay vị trí đặt lực từ  sang  sao cho  thì moment lực sẽ tăng lên gấp đôi

Từ đó, để đỡ tốn sức khi dùng mỏ lết vặn ốc, ta nên tác động lực tại vị trí cách con ốc (O) càng lớn càng tốt.

2. Phương trình tổng quát của mặt phẳng

Hoạt động 4: Trong không gian Oxyz, cho mặt phẳng (α). Gọi $\overrightarrow{n}=\left(A;B;C\right)$ là một vectơ pháp tuyến của (α) và M0(x0; y0; z0) là một điểm thuộc (α).

a) Một điểm M(x; y; z) thuộc (α) khi và chỉ khi hai vectơ $\overrightarrow{n}$ và $\overrightarrow{M_{0}M}$ có mối quan hệ gì?

b) Điểm M(x; y; z) thuộc (α) khi và chỉ khi tọa độ của nó thỏa mãn hệ thức nào?

Lời giải:

Luyện tập 4: Trong không gian Oxyz, phương trình nào trong các phương trình sau là phương trình tổng quát của một mặt phẳng?

a) x2 + 2y2 + 3z2 – 1 = 0;

b) $\frac{x}{2}-y+\frac{z}{3}+5=0$

c) xy + 5 = 0.

Lời giải:

Trong các phương trình trên, chỉ có phương trình $\frac{x}{2}-y+\frac{z}{3}+5=0$ có dạng Ax + By + Cz + D = 0 ($A=\frac{1}{2};B=-1;C=\frac{1}{3}$).

Vì vậy trong các phương trình trên, chỉ có phương trình $\frac{x}{2}-y+\frac{z}{3}+5=0$ là phương trình mặt phẳng.

Luyện tập 5: Trong không gian Oxyz, cho mặt phẳng (α): x + 2 = 0.

a) Điểm A(−2; 1; 0) có thuộc (α) hay không?

b) Hãy chỉ ra một vectơ pháp tuyến của (α).

Lời giải:

a) Do  nên điểm  thuộc 

b) Mặt phẳng  nhận  làm một vectơ pháp tuyến

3. Lập phương trình tổng quát của mặt phẳng

Hoạt động 5: Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M0(x0; y0; z0) và có vectơ pháp tuyến $\overrightarrow{n}=\left(A;B;C\right)$.

Dựa vào Hoạt động 4, hãy nêu phương trình của (α).

Lời giải:

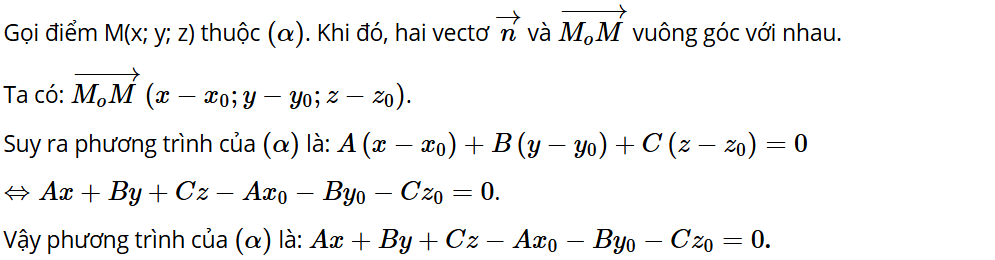
Luyện tập 6: Trong không gian Oxyz, viết phương trình mặt phẳng (α) đi qua điểm M(1; 2; −4) và vuông góc với trục Oz.

Lời giải:

Mặt phẳng (α) đi qua điểm M(1; 2; −4) và vuông góc với trục Oz nhận vectơ $\overrightarrow{k}=\left(0;0;1\right)$ làm vectơ pháp tuyến.

Do đó phương trình mặt phẳng (α) là: z + 4 = 0.

Hoạt động 6: Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M(x0; y0; z0) và biết cặp vectơ chỉ phương $\overrightarrow{u}=\left(a;b;c\right)$, $\overrightarrow{v}=\left(a^{\prime };b^{\prime };c^{\prime }\right)$

a) Hãy chỉ ra một vectơ pháp tuyến của mặt phẳng (α).

b) Viết phương trình mặt phẳng (α).

Lời giải:

a) Vì mặt phẳng  có cặp vectơ chỉ phương ,  nên  là một vectơ pháp tuyến của 

Ta có: 

Vậy một vectơ pháp tuyến của mặt phẳng  là: 

b) Mặt phẳng  đi qua điểm  và có vectơ pháp tuyến  nên có phương trình là:

Luyện tập 7: Trong không gian Oxyz, cho các điểm A(1; −2; −1), B(4; 1; 2), C(2; 3; 1). Viết phương trình mặt phẳng (α) đi qua điểm A(1; −2; −1) đồng thời song song với trục Oy và đường thẳng BC.

Lời giải:

Hoạt động 7: Trong không gian Oxyz, cho ba điểm không thẳng hàng: A(1; 2; 3), B(−1; 3; 4), C(2; −1; 2).

a) Hãy chỉ ra một cặp vectơ chỉ phương của mặt phẳng (ABC).

b) Viết phương trình mặt phẳng (ABC).

Lời giải:

a) Mặt phẳng  có một cặp vectơ chỉ phương là: 

 và 

b) Mặt phẳng  nhận  và  làm cặp vectơ chỉ phương nên có vecto pháp tuyến là:

Mặt phẳng  đi qua điểm  và nhận  làm một vectơ pháp tuyến nên có phương trình:

Luyện tập 8: (H.5.8) Trong không gian Oxyz, cho mặt phẳng (α) không đi qua gốc tọa độ và cắt ba trục Ox, Oy, Oz tương ứng tại các điểm A(a; 0; 0), B(0; b; 0), C(0; 0; c) (a, b, c ≠ 0).

Chứng minh rằng mặt phẳng (α) có phương trình: $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$

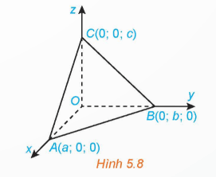
Lời giải:

Mặt phẳng (α) nhận $\overrightarrow{AB}=\left(-a;b;0\right)$ và $\overrightarrow{AC}=\left(-a;0;c\right)$ làm một cặp vectơ chỉ phương. Do đó mặt phẳng (α) nhận $\overrightarrow{n}=\left[\overrightarrow{AB},\overrightarrow{AC}\right]=\left(\left|\begin{array}{cc}b& 0\\ 0& c\end{array}\right|;\left|\begin{array}{cc}0& -a\\ c& -a\end{array}\right|;\left|\begin{array}{cc}-a& b\\ -a& 0\end{array}\right|\right)$$=\left(bc;ca;ba\right)$ làm một vectơ pháp tuyến.

Khi đó phương trình mặt phẳng (α) đi qua điểm A(a; 0; 0) và nhận $\overrightarrow{n}=\left(bc;ca;ba\right)$ làm vectơ pháp tuyến có dạng: bc(x – a) + cay + baz = 0 ⇔ bcx + cay + baz = abc$\iff \frac{bcx}{abc}+\frac{cay}{abc}+\frac{baz}{abc}=1$$\iff \frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$

Vận dụng 2: Trong tình huống mở đầu, hãy thực hiện các bước sau và trả lời câu hỏi đã được nêu ra.

a) Xác định tọa độ của vị trí M1, M2, M3 của vật tương ứng với các thời điểm t = 0, $t=\frac{\pi }{2}$, t = π.

b) Chứng minh rằng M1, M2, M3 không thẳng hàng và viết phương trình mặt phẳng (M1M2M3).

c) Vị trí M(cost – sint; cost + sint; cost) có luôn thuộc mặt phẳng (M1M2M3) hay không?

Lời giải:

4. Điều kiện để hai mặt phẳng vuông góc với nhau

Hoạt động 8: Trong không gian Oxyz, cho hai mặt phẳng: (α): Ax + By + Cz + D = 0, (β): A'x + B'y + C'z + D' = 0, với hai vectơ pháp tuyến $\overrightarrow{n}=\left(A;B;C\right),\overrightarrow{n^{\prime }}=\left(A^{\prime };B^{\prime };C^{\prime }\right)$ tương ứng.

a) Góc giữa hai mặt phẳng (α), (β) và góc giữa hai giá của $\overrightarrow{n},\overrightarrow{n^{\prime }}$ có mối quan hệ gì?

b) Hai mặt phẳng (α) và (β) vuông góc với nhau khi và chỉ khi hai vectơ pháp tuyến tương ứng $\overrightarrow{n},\overrightarrow{n^{\prime }}$ có mối quan hệ gì?

Lời giải:

a) Vì $\overrightarrow{n},\overrightarrow{n^{\prime }}$ lần lượt là vectơ pháp tuyến của mặt phẳng (α) và (β) nên giá của $\overrightarrow{n},\overrightarrow{n^{\prime }}$ lần lượt vuông góc với mặt phẳng (α) và (β).

Do đó góc giữa hai mặt phẳng (α), (β) bằng góc giữa hai giá của $\overrightarrow{n},\overrightarrow{n^{\prime }}$

b) Hai mặt phẳng (α) và (β) vuông góc với nhau khi và chỉ khi hai vectơ pháp tuyến tương ứng $\overrightarrow{n},\overrightarrow{n^{\prime }}$ vuông góc với nhau.

Luyện tập 9: Trong không gian Oxyz, hai mặt phẳng sau đây có vuông góc với nhau hay không? (α): 3x + y – z + 1 = 0, (β): 9x + 3y – 3z + 3 = 0.

Lời giải:

Hai mặt phẳng  có vecto pháp tuyến tương ứng là:

Ta có: 

Do đó 2 mặt phẳng  không vuông góc với nhau

Vận dụng 3: (H.5.10) Trong không gian Oxyz, sàn của một căn phòng có dạng hình tứ giác với bốn đỉnh O(0; 0; 0), A(2; 0; 0), B(2; 3; 0), $C\left(0;2\sqrt{2};0\right)$. Bốn bức tường của căn phòng đều vuông góc với sàn.

a) Viết phương trình bốn mặt phẳng tương ứng chứa bốn bức tường đó.

b) Trong bốn mặt phẳng tương ứng chứa bốn bức tường đó, hãy chỉ ra những cặp mặt phẳng vuông góc với nhau.

Lời giải:

5. Điều kiện để hai mặt phẳng song song với nhau

Hoạt động 9: Trong không gian Oxyz, cho hai mặt phẳng (α): Ax + By + Cz + D = 0, (β): A'x + B'y + C'x + D' = 0, với các vectơ pháp tuyến $\overrightarrow{n}=\left(A;B;C\right),\overrightarrow{n^{\prime }}=\left(A^{\prime };B^{\prime };C^{\prime }\right)$

Nếu hai mặt phẳng (α) và (β) song song hoặc trùng nhau thì các vectơ pháp tuyến $\overrightarrow{n},\overrightarrow{n^{\prime }}$ có mối quan hệ gì?

Lời giải:

Hai mặt phẳng (α) và (β) song song hoặc trùng nhau khi và chỉ khi các vectơ pháp tuyến $\overrightarrow{n},\overrightarrow{n^{\prime }}$ cùng phương. Tức là $\overrightarrow{n}=k\overrightarrow{n^{\prime }}$

Nếu D = kD' thì ta có mặt phẳng (α) và (β) trùng nhau.

Nếu D ≠ kD' thì ta có mặt phẳng (α) và (β) song song.

Vậy suy ra:

$\left(\alpha \right)//\left(\beta \right)\iff \{\begin{array}{c}\overrightarrow{n}=k\overrightarrow{n^{\prime }}\\ D\ne k{D}^{\prime }\end{array}$

$\left(\alpha \right)\equiv \left(\beta \right)\iff \{\begin{array}{c}\overrightarrow{n}=k\overrightarrow{n^{\prime }}\\ D=k{D}^{\prime }\end{array}$

Luyện tập 10: Trong không gian Oxyz, cho hai mặt phẳng: (α): 5x + 2y – 4z + 6 = 0 và (β): 10x + 4y – 2z + 12 = 0.

a) Hỏi (α) và (β) có song song với nhau hay không?

b) Chứng minh rằng điểm M(1; −3; 5) không thuộc mặt phẳng (α) nhưng thuộc mặt phẳng (β).

c) Viết phương trình mặt phẳng (P) đi qua M(1; −3; 5) và song song với (α).

Lời giải:

a) Hai mặt phẳng  có vecto pháp tuyến tương ứng là:

Do  và  nên hai mặt phẳng  không song song với nhau

b) Do  và  nên điểm  không thuộc mặt phẳng  nhưng thuộc mặt phẳng 

c) Do mặt phẳng  song song với  nên mặt phẳng  nhận  làm vectơ pháp tuyến

Mặt phẳng  đi qua điểm và nhận  làm vectơ pháp tuyến nên có phương trình:

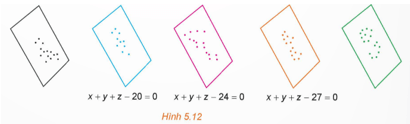
Vận dụng 4: Trong một kì thi tuyển sinh có ba môn thi Toán, Văn, Tiếng Anh. Trong không gian Oxyz, người ta biểu diễn kết quả thi của mỗi thí sinh bởi điểm có hoành độ, tung độ, cao độ tương ứng là điểm Toán, Văn, Tiếng Anh của thí sinh đó.

a) Chứng minh rằng các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn thi bằng 27 (nếu có) cùng thuộc mặt phẳng có phương trình x + y + z – 27 = 0.

b) Chứng minh rằng tồn tại một số mặt phẳng đôi một song song với nhau sao cho hai điểm biểu diễn ứng với thí sinh có tổng số điểm thi bằng nhau thì cùng thuộc một mặt phẳng trong số các mặt phẳng đó.

Lời giải:

6. Khoảng cách từ một điểm đến một mặt phẳng

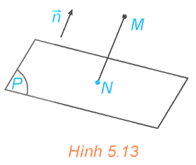
Hoạt động 10: Trong không gian Oxyz, cho điểm M(x0; y0; z0) và mặt phẳng (P): Ax + By + Cz + D = 0 có vectơ pháp tuyến $\overrightarrow{n}=\left(A;B;C\right)$. Gọi N là hình chiếu vuông góc của M trên (P) (H.5.13).

a) Giải thích vì sao tồn tại số k để $\overrightarrow{MN}=k\overrightarrow{n}$. Tính tọa độ của N theo k, tọa độ của M và các hệ số A, B, C, D.

b) Thay tọa độ của N vào phương trình mặt phẳng (P) để từ đó tính k theo tọa độ của M và các hệ số A, B, C, D.

c) Từ $\left|\overrightarrow{MN}\right|=\left|k\right|\left|\overrightarrow{n}\right|$, hãy tính độ dài của đoạn thẳng MN theo tọa độ của M và các hệ số A, B, C, D. Từ đó suy ra công thức tính khoảng cách từ điểm M đến mặt phẳng (P).

Lời giải:

a) Vì N là hình chiếu vuông góc của M trên (P) nên $MN\perp \left(P\right)$

Do đó $\overrightarrow{MN}$ sẽ cùng phương với vectơ pháp tuyến $\overrightarrow{n}$

Vậy tồn tại một số k sao cho $\overrightarrow{MN}=k\overrightarrow{n}$

Giả sử N(x1; y1; z1). Suy ra $\overrightarrow{MN}=\left(x_1-x_0;y_1-y_0;z_1-z_0\right)$

Vì $\overrightarrow{MN}=k\overrightarrow{n}$ nên $\{\begin{array}{c}{x}_1-x_0=kA\\ y_1-y_0=kB\\ z_1-z_0=kC\end{array}$$\iff \{\begin{array}{c}{x}_1=x_0+kA\\ y_1=y_0+kB\\ z_1=z_0+kC\end{array}$

b) Thay tọa độ điểm N vào (P), ta được

A(x0 + kA) + B(y0 + kB) + C(z0 + kC) + D = 0

⇔ k(A2 + B2 + C2) + Ax0 + By0 + Cz0 + D = 0

$\iff k=\frac{-A{x}_0-B{y}_0-C{z}_0-D}{A^2+B^2+C^2}$

c) Ta có $\left|\overrightarrow{MN}\right|=\left|k\right|\left|\overrightarrow{n}\right|$$\iff \left|\overrightarrow{MN}\right|=\left|k\right|\sqrt{A^2+B^2+C^2}$

Mà $k=\frac{-A{x}_0-B{y}_0-C{z}_0-D}{A^2+B^2+C^2}$ nên $MN=\left|\frac{-A{x}_0-B{y}_0-C{z}_0-D}{A^2+B^2+C^2}\right|\sqrt{A^2+B^2+C^2}$

$\iff MN=\frac{\left|}{A{x}_0+B{y}_0+C{z}_0+D}$

Do đó khoảng cách từ điểm M đến mặt phẳng (P) là $d=\frac{\left|}{A{x}_0+B{y}_0+C{z}_0+D}$

Luyện tập 11: Trong không gian Oxyz, cho hai mặt phẳng (P): x + 3y + z + 2 = 0 và (Q): x + 3y + z + 5 = 0.

a) Chứng minh rằng (P) và (Q) song song với nhau.

b) Lấy một điểm thuộc (P), tính khoảng cách từ điểm đó đến (Q). Từ đó tính khoảng cách giữa hai mặt phẳng (P) và (Q).

Lời giải:

a) Hai mặt phẳng  có vecto pháp tuyến tương ứng là:

Do  và  nên hai mặt phẳng  song song với nhau

b) Lấy điểm  thuộc mặt phẳng 

Khoảng cách từ điểm M đến  là:

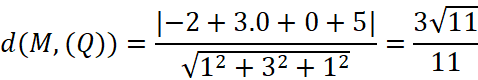
Vì hai mặt phẳng  song song với nhau nên khoảng cách giữa hai mặt phẳng  và  bằng khoảng cách từ điểm M đến , do đó:

Vận dụng 5: (H.5.14) Góc quan sát ngang của một camera là 115°. Trong không gian Oxyz, camera được đặt tại điểm C(1; 2; 4) và chiếu thẳng về phía mặt phẳng (P): x + 2y + 2z + 3 = 0. Hỏi vùng quan sát được trên mặt phẳng (P) của camera là hình tròn có bán kính bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất)

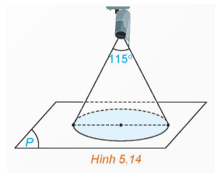
Lời giải:

Bài tập

Bài 5.1: Trong không gian Oxyz, viết phương trình mặt phẳng đi qua điểm M(1; 2; −1) và vuông góc với trục Ox.

Lời giải:

Gọi mặt phẳng cần tìm là mặt phẳng (P).

Vì mặt phẳng (P) vuông góc với trục Ox nên nhận $\overrightarrow{i}=\left(1;0;0\right)$ làm một vectơ pháp tuyến.

Mặt phẳng (P) đi qua điểm M(1; 2; −1) và nhận $\overrightarrow{i}=\left(1;0;0\right)$ làm một vectơ pháp tuyến có phương trình là: x – 1 = 0.

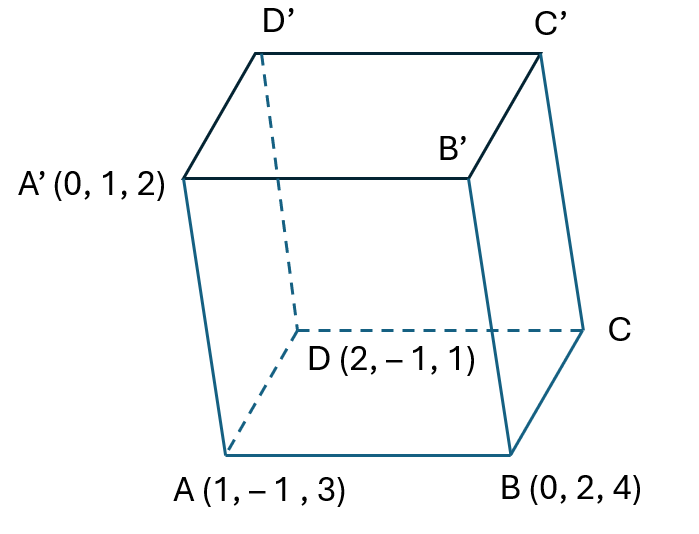
Bài 5.2: Trong không gian Oxyz, cho hình hộp ABCD.A'B'C'D', với A(1; −1; 3), B(0; 2; 4), D(2; −1; 1), A'(0; 1; 2).

a) Tìm tọa độ các điểm C, B', D'.

b) Viết phương trình mặt phẳng (CB'D').

Lời giải:

a) Ta có:  

Ta có:  

và 

và 

Mặt phẳng  nhận  và  làm cặp vectơ chỉ phương nên có vecto pháp tuyến là:

Mặt phẳng  đi qua điểm  và nhận  làm một vectơ pháp tuyến nên có phương trình:

Bài 5.3: Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M(1; −1; 5) và vuông góc với hai mặt phẳng (Q): 3x + 2y – z = 0, (R): x + y – z = 0.

Lời giải:

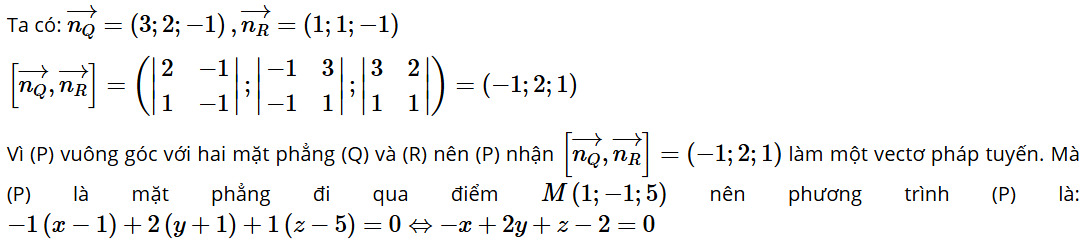
Bài 5.4: Trong không gian Oxyz, viết phương trình mặt phẳng đi qua M(2; 3; −1), song song với trục Ox và vuông góc với mặt phẳng (Q): x + 2y – 3z + 1 = 0.

Lời giải:

Gọi mặt phẳng cần tìm là mặt phẳng (P).

Ta có $\overrightarrow{i}=\left(1;0;0\right)$ và $\overrightarrow{n_Q}=\left(1;2;-3\right)$

Vì (P) // Ox và (P) ⊥ (Q) nên $\overrightarrow{n_P}=\left[\overrightarrow{i},\overrightarrow{n_Q}\right]=\left(0;3;2\right)$

Mặt phẳng đi qua M(2; 3; −1) và nhận $\overrightarrow{n_P}=\left(0;3;2\right)$ làm một vectơ pháp tuyến có phương trình là: 3(y – 3) + 2(z + 1) = 0 ⇔ 3y + 2z – 7 = 0.

Bài 5.5: Trong không gian Oxyz, tính khoảng cách từ gốc tọa độ đến mặt phẳng (P): 2x + 2y – z + 1 = 0.

Lời giải:

Khoảng cách từ gốc tọa độ đến mặt phẳng  là:

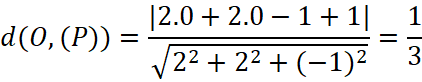
Bài 5.6: Trong không gian Oxyz, cho hai mặt phẳng (P): x + y + z + 2 = 0, (Q): x + y + z + 6 = 0. Chứng minh rằng hai mặt phẳng đã cho song song với nhau và tính khoảng cách giữa hai mặt phẳng đó.

Lời giải:

Vì $\overrightarrow{n_P}=\overrightarrow{n_Q}=\left(1;1;1\right)$ và 2 ≠ 6 nên (P) // (Q).

Lấy M(0; 0; −2) ∈ (P).

Khi đó $d\left(M,\left(Q\right)\right)=d\left(\left(P\right),\left(Q\right)\right)=\frac{\left|}{-2+6}=\frac{4}{\sqrt{3}}$

Bài 5.7: Trong không gian Oxyz, cho hai mặt phẳng (P): x + 3y – z = 0, (Q): x – y – 2z + 1 = 0.

a) Chứng minh rằng hai mặt phẳng (P) và (Q) vuông góc với nhau.

b) Tìm điểm M thuộc trục Ox và cách đều hai mặt phẳng (P) và (Q).

Lời giải:

Bài 5.8: Bác An dự định làm bốn mái của ngôi nhà sao cho chúng là bốn mặt bên của một hình chóp đều và các mái nhà kề nhau thì vuông góc với nhau. Hỏi ý tưởng trên có thực hiện được không?

Lời giải:

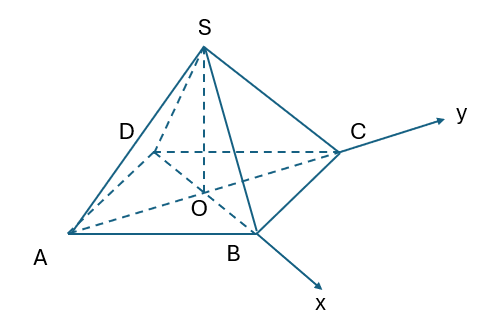
Đặt hệ trục toạ độ như hình bên:

Hình chóp đều  có đáy là hình vuông  với độ dài cạnh a và cạnh bên với độ dài b

Ta cần xác định xem 2 mặt phẳng  có vuông góc với nhau không

Do  là hình vuông nên  

Xét  vuông tại O nên: 

Khi đó:

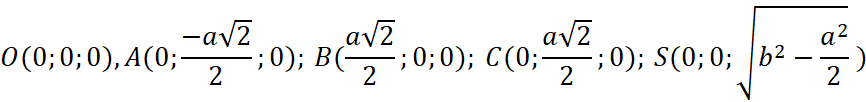
Mặt phẳng  nhận  và  làm cặp vectơ chỉ phương nên có vecto pháp tuyến là:

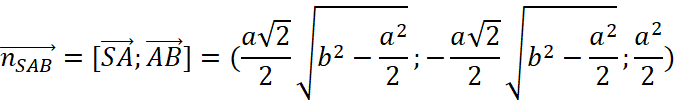
Mặt phẳng  nhận  và  làm cặp vectơ chỉ phương nên có vecto pháp tuyến là:

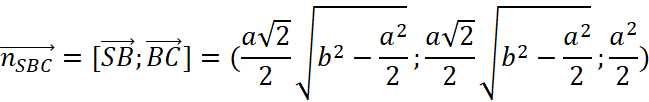
Ta có: 

..=

Do đó 2 mặt phẳng  không vuông góc với nhau

Vậy không thể thực hiện được ý tưởng trên.

Bài 5.9: Trong không gian Oxyz, một ngôi nhà có sàn nhà thuộc mặt phẳng Oxy, trần nhà tầng 1 thuộc mặt phẳng z – 1 = 0, mái nhà tầng 2 thuộc mặt phẳng x + y + 50z – 100 = 0. Hỏi trong ba mặt phẳng tương ứng chứa sàn nhà, trần tầng 1, mái tầng 2, hai mặt phẳng nào song song với nhau.

Lời giải:

Vì mặt phẳng Oxy vuông góc với Oz nên mặt phẳng Oxy nhận $\overrightarrow{k}=\left(0;0;1\right)$ làm một vectơ pháp tuyến.

Vì mặt phẳng Oxy đi qua điểm O(0; 0; 0) và có vectơ pháp tuyến $\overrightarrow{k}=\left(0;0;1\right)$ nên có phương trình là: z – 0 = 0 hay z = 0.

Mặt phẳng z – 1 = 0 có $\overrightarrow{n_1}=\left(0;0;1\right)$

Vì $\overrightarrow{n_1}=\overrightarrow{k}$ và 0 ≠ −1 nên mặt phẳng chứa sàn nhà song song với trần tầng 1.