Giải SGK Toán 12 Kết nối tri thức Bài 16: Công thức tính góc trong không gian

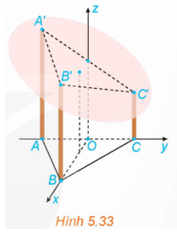
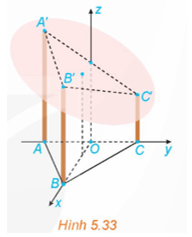
Mở đầu: Một mái nhà hình tròn được đặt trên ba cây cột trụ (H.5.33). Các cây cột vuông góc với mặt sàn nhà phẳng và có độ cao lần lượt là 7 m, 6 m, 5 m. Ba chân cột là ba đỉnh của một tam giác đều trên mặt sàn nhà với cạnh dài 4 m. Hỏi mái nhà nghiêng với mặt sàn nhà một góc bao nhiêu độ?

Lời giải:

Sau khi học xong bài này, ta giải quyết bài toán này như sau:

Chọn hệ trục tọa độ như hình vẽ với O là trung điểm của AC.

Ta có: A(0; −2; 0), B($2\sqrt{3}$; 0; 0), C(0; 2; 0), A'(0; −2; 7), B'($2\sqrt{3}$; 0; 6), C'(0; 2; 5).

Ta có $\overrightarrow{AB}=\left(2\sqrt{3};2;0\right),\overrightarrow{AC}=\left(0;4;0\right),\overrightarrow{A^{\prime }{B}^{\prime }}=\left(2\sqrt{3};2;-1\right),\overrightarrow{A^{\prime }{C}^{\prime }}=\left(0;4;-2\right)$

Có $\left[\overrightarrow{AB},\overrightarrow{AC}\right]=\left(\left|\begin{array}{cc}2& 0\\ 4& 0\end{array}\right|,\left|\begin{array}{cc}0& 2\sqrt{3}\\ 0& 0\end{array}\right|,\left|\begin{array}{cc}2\sqrt{3}& 2\\ 0& 4\end{array}\right|\right)$$=\left(0;0;8\sqrt{3}\right)$

$\left[\overrightarrow{A^{\prime }{B}^{\prime }},\overrightarrow{A^{\prime }{C}^{\prime }}\right]=\left(\left|\begin{array}{cc}2& -1\\ 4& -2\end{array}\right|,\left|\begin{array}{cc}-1& 2\sqrt{3}\\ -2& 0\end{array}\right|,\left|\begin{array}{cc}2\sqrt{3}& 2\\ 0& 4\end{array}\right|\right)$$=\left(0;4\sqrt{3};8\sqrt{3}\right)$

Mặt phẳng (ABC) có một vectơ pháp tuyến là $\frac{1}{8\sqrt{3}}\left[\overrightarrow{AB},\overrightarrow{AC}\right]=\left(0;0;1\right)$

Mặt phẳng (A'B'C') có một vectơ pháp tuyến là $\frac{1}{4\sqrt{3}}\left[\overrightarrow{A^{\prime }{B}^{\prime }},\overrightarrow{A^{\prime }{C}^{\prime }}\right]=\left(0;1;2\right)$

Do đó $\cos \left(\left(ABC\right),\left(A^{\prime }{B}^{\prime }{C}^{\prime }\right)\right)=\frac{\left|}{2}=\frac{2}{\sqrt{5}}$ ⇒ ((ABC), (A'B'C')) ≈ 26,6°.

Suy ra mái nhà nghiêng với mặt sàn nhà một góc khoảng 26,6°.

1. Công thức tính góc giữa hai đường thẳng

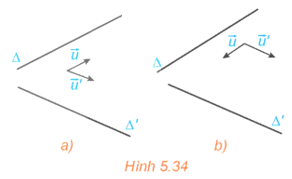
Hoạt động 1: Trong không gian Oxyz, cho hai đường thẳng ∆ và ∆' tương ứng có các vectơ chỉ phương $\overrightarrow{u}=\left(a;b;c\right),\overrightarrow{u^{\prime }}=\left(a^{\prime };b^{\prime };c^{\prime }\right)$ (H.5.34).

a) Hãy tìm mối quan hệ giữa các góc (∆, ∆') và $\left(\overrightarrow{u},\overrightarrow{u^{\prime }}\right)$.

b) Có nhận xét gì về mối quan hệ giữa cos(∆, ∆') và $\left|\cos \left(\overrightarrow{u},\overrightarrow{u^{\prime }}\right)\right|$?

Lời giải:

a) Ta có:  Hai đường thẳng  và  tương ứng có các vectơ chỉ phương là  nên giá của  song song với  và giá của  song song với 

H5.34a: ;

H5.34b: ;

b)

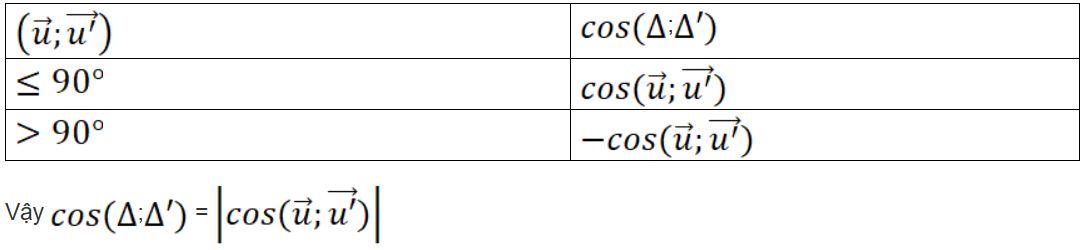
Luyện tập 1: Trong không gian Oxyz, tính góc giữa trục Oz và đường thẳng $\Delta :\frac{x-3}{1}=\frac{y+1}{2}=\frac{z-1}{-2}$

Lời giải:

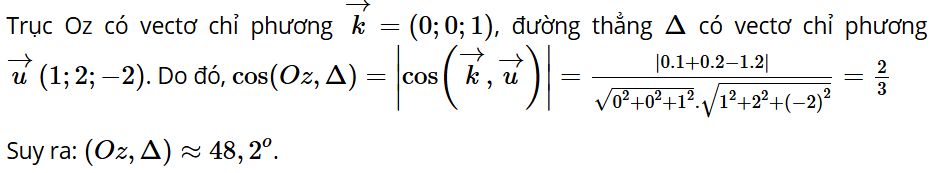
2. Công thức tính góc giữa đường thẳng và mặt phẳng

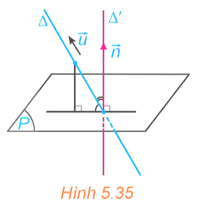
Hoạt động 2: Trong không gian Oxyz, cho đường thẳng ∆ và mặt phẳng (P). Xét $\overrightarrow{u}=\left(a;b;c\right)$ là một vectơ chỉ phương của ∆ và $\overrightarrow{n}=\left(A;B;C\right)$ (với giá ∆') là một vectơ pháp tuyến của (P). (H.5.35)

a) Hãy tìm mối quan hệ giữa các góc (∆, (P)) và (∆, ∆').

b) Có nhận xét gì về mối quan hệ giữa sin(∆, ∆') và $\left|\cos \left(\overrightarrow{u},\overrightarrow{n}\right)\right|$?

Lời giải:

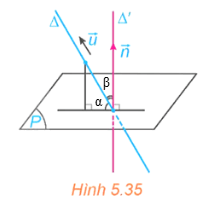
a) Gọi α = (∆, (P)), β = (∆, ∆').

Có α + β = 90°. Suy ra (∆, ∆') = 90° − (∆, (P)).

b) Có sin(∆, ∆') $=\left|\cos \left(\overrightarrow{u},\overrightarrow{n}\right)\right|$.

Luyện tập 2: Trong không gian Oxyz, tính góc giữa đường thẳng ∆ và mặt phẳng (P), với: $\Delta :\frac{x+2}{-1}=\frac{y-4}{2}=\frac{z+1}{1}$, (P): x – y + z – 1 = 0.

Lời giải:

Đường thẳng  có vecto chỉ phương là  và mặt phẳng (P) có vecto pháp tuyến 

Khi đó:  

Vậy đường thẳng  tạo với mặt phẳng  góc 

3. Công thức tính góc giữa hai mặt phẳng

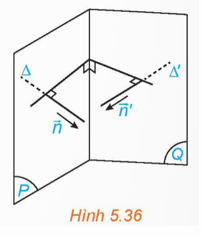
Hoạt động 3: Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là $\overrightarrow{n}=\left(A;B;C\right)$, $\overrightarrow{n^{\prime }}=\left(A^{\prime };B^{\prime };C^{\prime }\right)$. Lấy các đường thẳng ∆, ∆' tương ứng có vectơ chỉ phương $\overrightarrow{n},\overrightarrow{n^{\prime }}$. (H.5.36)

a) Góc giữa hai mặt phẳng (P) và (Q) và góc giữa hai đường thẳng ∆ và ∆' có mối liên hệ gì?

b) Tính côsin của góc giữa hai mặt phẳng (P) và (Q).

Lời giải:

Luyện tập 3: Trong không gian Oxyz, tính góc giữa hai mặt phẳng (P): $x-\sqrt{2}y+z-2=0$ và (Oxz): y = 0.

Lời giải:

Mặt phẳng (P) có vectơ pháp tuyến $\overrightarrow{n}=\left(1;-\sqrt{2};1\right)$

Mặt phẳng (Oxz) có vectơ pháp tuyến $\overrightarrow{n^{\prime }}=\left(0;1;0\right)$

Có $\cos \left(\left(P\right),\left(Oxz\right)\right)=\frac{\left|}{1.0-\sqrt{2}.1+1.0}=\frac{\sqrt{2}}{2}$

Suy ra ((P), (Oxz)) = 45°.

Vận dụng: Hãy trả lời câu hỏi đã được nêu ra trong tình huống mở đầu.

Lời giải:

Chọn hệ trục tọa độ như hình vẽ, O là trung điểm của AC.

Ta có: A(0; −2; 0), B($2\sqrt{3}$; 0; 0), C(0; 2; 0), A'(0; −2; 7), B'($2\sqrt{3}$; 0; 6), C'(0; 2; 5).

Ta có $\overrightarrow{AB}=\left(2\sqrt{3};2;0\right),\overrightarrow{AC}=\left(0;4;0\right),\overrightarrow{A^{\prime }{B}^{\prime }}=\left(2\sqrt{3};2;-1\right),\overrightarrow{A^{\prime }{C}^{\prime }}=\left(0;4;-2\right)$

Có $\left[\overrightarrow{AB},\overrightarrow{AC}\right]=\left(\left|\begin{array}{cc}2& 0\\ 4& 0\end{array}\right|,\left|\begin{array}{cc}0& 2\sqrt{3}\\ 0& 0\end{array}\right|,\left|\begin{array}{cc}2\sqrt{3}& 2\\ 0& 4\end{array}\right|\right)$$=\left(0;0;8\sqrt{3}\right)$

$\left[\overrightarrow{A^{\prime }{B}^{\prime }},\overrightarrow{A^{\prime }{C}^{\prime }}\right]=\left(\left|\begin{array}{cc}2& -1\\ 4& -2\end{array}\right|,\left|\begin{array}{cc}-1& 2\sqrt{3}\\ -2& 0\end{array}\right|,\left|\begin{array}{cc}2\sqrt{3}& 2\\ 0& 4\end{array}\right|\right)$$=\left(0;4\sqrt{3};8\sqrt{3}\right)$

Mặt phẳng (ABC) có một vectơ pháp tuyến là $\frac{1}{8\sqrt{3}}\left[\overrightarrow{AB},\overrightarrow{AC}\right]=\left(0;0;1\right)$

Mặt phẳng (A'B'C') có một vectơ pháp tuyến là $\frac{1}{4\sqrt{3}}\left[\overrightarrow{A^{\prime }{B}^{\prime }},\overrightarrow{A^{\prime }{C}^{\prime }}\right]=\left(0;1;2\right)$

Do đó $\cos \left(\left(ABC\right),\left(A^{\prime }{B}^{\prime }{C}^{\prime }\right)\right)=\frac{\left|}{2}=\frac{2}{\sqrt{5}}$ => ((ABC), (A'B'C')) ≈ 26,6°.

Suy ra mái nhà nghiêng với mặt sàn nhà một góc khoảng 26,6°.

Bài tập

Bài 5.20: Trong không gian Oxyz, tính góc giữa hai đường thẳng ${\Delta }_1:\{\begin{array}{c}x=1+2t\\ y=1-t\\ z=2+3t\end{array}$ và ${\Delta }_2:\frac{x-2}{-1}=\frac{x+1}{1}=\frac{z-2}{2}$

Lời giải:

Hai đường thẳng  tương ứng có các vectơ chỉ phương là .

Khi đó:  

Vậy 

Bài 5.21: Trong không gian Oxyz, tính góc giữa trục Oz và mặt phẳng (P): x + 2y – z – 1 = 0.

Lời giải:

Bài 5.22: Tính góc giữa đường thẳng $\Delta :\frac{x+1}{-1}=\frac{y-3}{2}=\frac{z+2}{3}$ và mặt phẳng (P): x + y + z + 3 = 0.

Lời giải:

Đường thẳng ∆ có vectơ chỉ phương là $\overrightarrow{u}=\left(-1;2;3\right)$

Mặt phẳng (P) có vectơ pháp tuyến là $\overrightarrow{n}=\left(1;1;1\right)$

Có $\sin \left(\Delta ,\left(P\right)\right)=\frac{\left|}{-1.1+2.1+3.1}=\frac{4}{\sqrt{42}}$

Suy ra (∆, (P)) ≈ 38,1°.

Bài 5.23: Kim tự tháp Kheops ở Ai Cập có dạng hình chóp S.ABCD, có đáy là hình vuông với cạnh dài 230 m, các cạnh bên bằng nhau và dài 219 m (theo britannica.com) (H.5.38). Tính góc giữa hai mặt phẳng (SAB) và (SBC).

Lời giải:

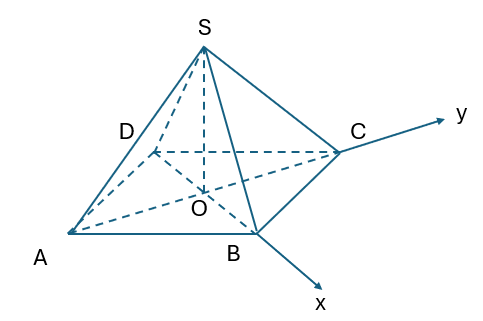
Do  là hình vuông nên  

Xét  vuông tại O nên:

Khi đó:

Ta có: 

Mặt phẳng  nhận  và  làm cặp vectơ chỉ phương nên có vecto pháp tuyến là:

Mặt phẳng  nhận  và  làm cặp vectơ chỉ phương nên có vecto pháp tuyến là:

Khi đó:

Vậy góc giữa hai mặt phẳng  là .

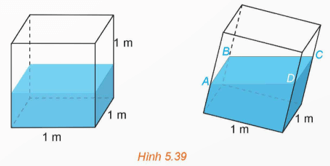
Bài 5.24: (H.5.39) Trong một bể hình lập phương cạnh 1 m có chứa một ít nước. Người ta đặt đáy bể nghiêng so với mặt phẳng nằm ngang. Biết rằng, lúc đó mặt nước có dạng hình bình hành ABCD và khoảng cách từ các điểm A, B, C đến đáy bể tương ứng là 40 cm, 44 cm, 48 cm.

a) Khoảng cách từ điểm D đến đáy bể bằng bao nhiêu centimét? (Tính gần đúng, lấy giá trị nguyên).

b) Đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ?

Lời giải: