Giải SGK Toán 12 Kết nối tri thức Bài 19: Công thức xác suất toàn phần và công thức Bayes

1. Công thức xác suất toàn phần

Hoạt động 1: Hình thành công thức xác suất toàn phần

Gọi A là biến cố “Trời mưa” và B là biến cố “Bán hết vé” trong tình huống mở đầu.

a) Tính P(A), $P\left(\overline{A}\right)$, P(B | A), $P\left(B|\overline{A}\right)$.

b) Trong hai xác suất P(A) và P(B), nhà tổ chức sự kiện quan tâm đến xác suất nào nhất?

Lời giải:

a) Với A là biến cố “Trời mưa” và B là biến cố “Bán hết vé”.

Theo bài ra ta có: P(A) = 0,75. Suy ra P($\overline{A}$) = 1 – P(A) = 1 – 0,75 = 0,25.

Lại có:

+) nếu trời mưa thì xác suất bán hết vé là 0,4. Vậy P(B | A) = 0,4.

+) nếu trời không mưa thì xác suất bán hết vé là 0,9. Vậy $P\left(B|\overline{A}\right)$ = 0,9.

b) Nhà tổ chức quan tâm tới P(B) nhất.

Luyện tập 1: Trở lại tình huống mở đầu Mục 1. Tính xác suất để nhà tổ chức sự kiện bán hết vé.

Lời giải:

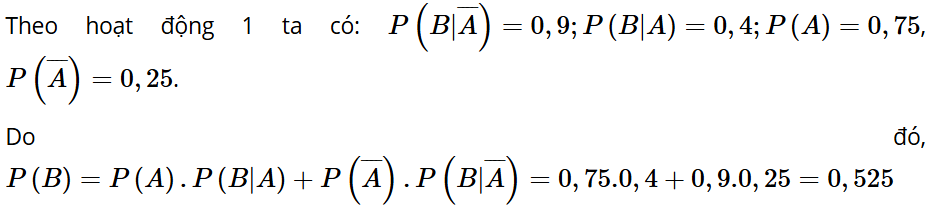
Luyện tập 2: Trở lại Ví dụ 1. Sử dụng sơ đồ hình cây, hãy mô tả cách tính xác suất để thứ Tư, ông An đi làm bằng xe buýt.

Lời giải:

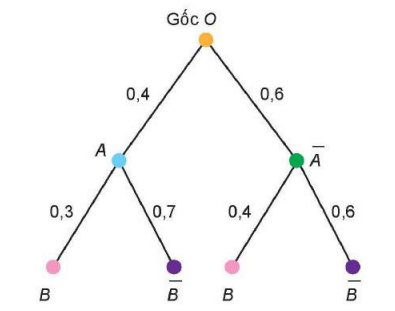
A là biến cố: “Thứ Ba, ông An đi làm bằng xe máy”; B là biến cố: “Thứ Tư, ông An đi làm bằng xe máy”

Khi đó  là biến cố: “Thứ Ba, ông An đi làm bằng xe buýt”; là biến cố: “Thứ Tư, ông An đi làm bằng xe buýt

Ta cần tính  

Có 2 nhánh cây đi tới  là  và 

Vậy: 

Vận dụng: Hình dạng hạt của đậu Hà Lan có hai kiểu hình: hạt trơn và hạt nhăn, có hai gene ứng với hai kiểu hình này là gene trội B và gene lặn b.

Khi cho lai hai cây đậu Hà Lan, cây con lấy ngẫu nhiên một cách độc lập một gene từ cây bố và một gene từ cây mẹ để hình thành một cặp gene. Giả sử cây bố và cây mẹ được chọn ngẫu nhiên từ một quần thể các cây đậu Hà Lan, ở đó tỉ lệ cây mang kiểu gene bb, Bb tương ứng là 40% và 60%. Tính xác suất để cây con có kiểu gene bb.

Lời giải:

Gọi A là biến cố: “Cây bố có kiểu gene bb”;

       M là biến cố: “Cây con lấy gene b từ cây bố”;

       N là biến cố: “Cây con lấy gene b từ cây mẹ”;

       E là biến cố: “Cây con có kiểu gene bb”.

Theo giả thiết, M và N độc lập nên P(E) = P(M) ∙ P(N).

Tính P(M): Ta áp dụng công thức xác suất toàn phần:

P(M) = P(A) ∙ P(M | A) + P($\overline{A}$) ∙ P(M | $\overline{A}$). (*)

Ta có P(A) = 0,4; P($\overline{A}$) = 0,6.

P(M | A) là xác suất để cây con lấy gene b từ cây bố với điều kiện cây bố có kiểu gene bb. Do đó, P(M | A) = 1.

P(M | $\overline{A}$) là xác suất để cây con lấy gene b từ cây bố với điều kiện cây bố có kiểu gene Bb. Do đó, P(M | $\overline{A}$) = 0,5.

Thay vào (*) ta được: P(M) = 0,4 ∙ 1 + 0,6 ∙ 0,5 = 0,7.

Tương tự tính được P(N) = 0,7.

Vậy P(E) = P(M) ∙ P(N) = 0,7 ∙ 0,7 = 0,49.

Từ kết quả trên suy ra trong một quần thể các cây đậu Hà Lan, mà ở đó tỉ lệ cây bố và cây mẹ mang kiểu gene bb, Bb tương ứng là 40% và 60%, thì tỉ lệ cây con có kiểu gene bb là khoảng 49%.

Luyện tập 3: Với giả thiết như phần vận dụng:

Hình dạng hạt của đậu Hà Lan có hai kiểu hình: hạt trơn và hạt nhẵn, có hai gene ứng với hai kiểu hình này là gene trội B và gene lặn b.

Khi cho lai hai cây đậu Hà Lan, cây con lấy ngẫu nhiên một cách độc lập một gene từ cây bố và một gene từ cây mẹ để hình thành một cặp gene. Giả sử cây bố và cây mẹ được chọn ngẫu nhiên từ một quần thể các cây đậu Hà Lan, ở đó tỉ lệ cây mang kiểu gene bb, Bb tương ứng là 40% và 60%.

a) Hãy ước lượng tỉ lệ cây con có kiểu gene BB.

b) Sử dụng kết quả của vận dụng trên và câu a, hãy ước lượng tỉ lệ cây con có kiểu gene Bb.

Lời giải:

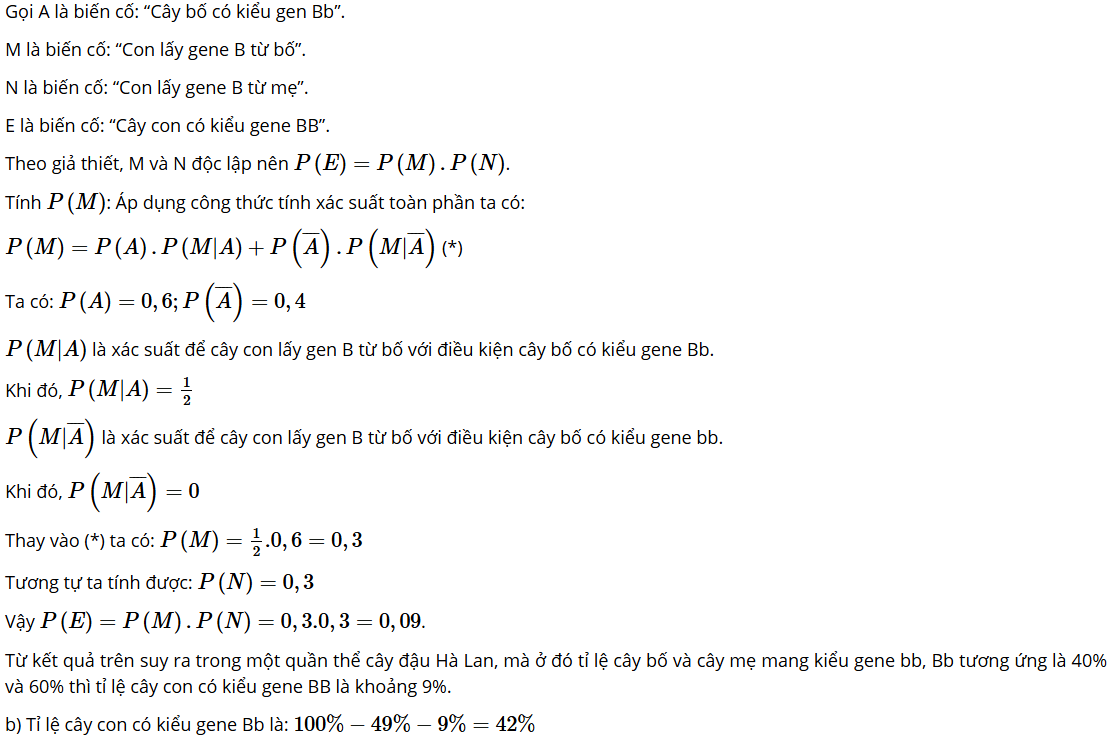
2. Công thức bayer

Hoạt động 2: Phân biệt P(A | B) và P(B | A). Tình huống mở đầu

Trong Y học, để chẩn đoán bệnh X nào đó, người ta thường dùng một xét nghiệm. Xét nghiệm dương tính, tức là xét nghiệm đó kết luận một người mắc bệnh X. Xét nghiệm âm tính, tức là xét nghiệm đó kết luận một người không mắc bệnh X. Vì không có một xét nghiệm nào tuyệt đối đúng nên trên thực tế có thể xảy ra hai sai lầm sau:

– Xét nghiệm dương tính nhưng thực tế người xét nghiệm không mắc bệnh. Ta gọi đây là dương tính giả.

– Xét nghiệm âm tính nhưng thực tế người xét nghiệm lại mắc bệnh. Ta gọi đây là âm tính giả.

Ông M đi xét nghiệm bệnh hiểm nghèo X. Biết rằng, nếu một người mắc bệnh X thì với xác suất 0,95 xét nghiệm cho dương tính; nếu một người không bị bệnh X thì với xác suất 0,01 xét nghiệm cho dương tính.

Xét nghiệm của ông M cho kết quả dương tính. Ông M hoảng hốt khi nghĩ rằng mình có xác suất 0,95 mắc bệnh hiểm nghèo X.

Trong tình huống mở đầu Mục 2, gọi A là biến cố: “Ông M mắc bệnh hiểm nghèo X”; B là biến cố: “Xét nghiệm cho kết quả dương tính”.

a) Nêu các nội dung còn thiếu tương ứng với “(?)” để hoàn thành các câu sau đây:

Ÿ P(A | B) là xác suất để (?) với điều kiện (?);

Ÿ P(B | A) là xác suất để (?) với điều kiện (?).

b) 0,95 là P(A | B) hay P(B | A)? Có phải ông M có xác suất 0,95 mắc bệnh hiểm nghèo X không?

Lời giải:

Luyện tập 4: Trong một kho rượu có 30% là rượu loại I. Chọn ngẫu nhiên một chai rượu đưa cho ông Tùng, một người sành rượu, để nếm thử. Biết rằng, một chai rượu loại I có xác suất 0,9 để ông Tùng xác nhận là loại I; một chai rượu không phải loại I có xác suất 0,95 để ông Tùng xác nhận đây không phải rượu loại I. Sau khi nếm, ông Tùng xác nhận đây là rượu loại I. Tính xác suất để chai rượu đúng là rượu loại I.

Lời giải:

Gọi A là biến cố:”Chai rượu đúng là rượu loại I”;

B là biến cố:”Ông Tùng xác nhận đây là rượu loại I”

Ta cần tính 

Theo công thức Bayes, ta cần biết: 

Ta có: 

 là xác suất để một chai rượu mà ông Tùng xác nhận là loại I với điều kiện đây đúng là rượu loại I 

 là xác suất để một chai rượu mà ông Tùng xác nhận không phải là loại I với điều kiện đây không phải loại rượu loại I 

Thay vào công thức Bayes ta có:

Luyện tập 5: Trở lại tình huống mở đầu Mục 2. Thống kê cho thấy tỉ lệ dân số mắc bệnh hiểm nghèo X là 0,2%.

a) Trước khi tiến hành xét nghiệm, xác suất mắc bệnh hiểm nghèo X của ông M là bao nhiêu?

b) Sau khi xét nghiệm cho kết quả dương tính, xác suất mắc bệnh hiểm nghèo X của ông M là bao nhiêu?

Lời giải:

a) Vì thống kê cho thấy tỉ lệ dân số mắc bệnh hiểm nghèo X là 0,2% nên trước khi tiến hành xét nghiệm, xác suất mắc bệnh hiểm nghèo X của ông M là p = 0,2% = 0,002.

b) Gọi A là biến cố: “Ông M mắc bệnh hiểm nghèo X”; B là biến cố: “Xét nghiệm cho kết quả dương tính”.

Khi đó xác suất mắc bệnh hiểm nghèo X của ông M sau khi xét nghiệm cho kết quả dương tính chính là xác suất P(A | B).

Áp dụng công thức ta có

P(A | B) = $\frac{P\left(A\right)\cdot P\left(B|A\right)}{P\left(A\right)\cdot P\left(B|A\right)+P\left(\overline{A}\right)\cdot P\left(B|\overline{A}\right)}$.

Theo câu a) ta có: P(A) = p = 0,002. Suy ra P($\overline{A}$) = 1 – P(A) = 1 – 0,002 = 0,998.

P(B | A) là xác suất xét nghiệm cho kết quả dương tính nếu ông M mắc bệnh hiểm nghèo X. Theo bài ra ta có P(B | A) = 0,95.

P(B | $\overline{A}$) là xác suất xét nghiệm cho kết quả dương tính nếu ông M không mắc bệnh hiểm nghèo X. Theo bài ra ta có P(B | $\overline{A}$) = 0,01.

Khi đó, thay vào công thức Bayes ta được

$P\left(A\text{|}B\right)=\frac{\mathrm{0,002}\cdot \mathrm{0,95}}{\mathrm{0,002}\cdot \mathrm{0,95}+\mathrm{0,998}\cdot \mathrm{0,01}}\approx \mathrm{0,16}$.

Vậy sau khi xét nghiệm cho kết quả dương tính, xác suất mắc bệnh hiểm nghèo X của ông M là khoảng 0,16.

Bài tập

Bài 6.7: Trong quân sự, một máy bay chiến đấu của đối phương có thể xuất hiện ở vị trí X với xác suất 0,55. Nếu máy bay đó không xuất hiện ở vị trí X thì nó xuất hiện ở vị trí Y. Để phòng thủ, các bệ phóng tên lửa được bố trí tại các vị trí X và Y. Khi máy bay đối phương xuất hiện ở vị trí X hoặc Y thì tên lửa sẽ được phóng để hạ máy bay đó.

Xét phương án tác chiến sau: Nếu máy bay xuất hiện tại X thì bắn 2 quả tên lửa và nếu máy bay xuất hiện tại Y thì bắn 1 quả tên lửa.

Biết rằng, xác suất bắn trúng máy bay của mỗi quả tên lửa là 0,8 và các bệ phóng tên lửa hoạt động độc lập. Máy bay bị bắn hạ nếu nó trúng ít nhất 1 quả tên lửa. Tính xác suất bắn hạ máy bay đối phương trong phương án tác chiến nêu trên.

Lời giải:

Gọi A là biến cố:”Máy bay chiến đấu của đối phương xuất hiện tại X”

B là biến cố:”Máy bay chiến đấu của đối phương bị bắn hạ”

Ta cần tính 

Theo công thức xác suất toàn phần, ta có:

 là xác suất máy bay chiến đấu của đối phương có thể xuất hiện ở vị trí X

 là xác suất máy bay chiến đấu của đối phương bị bắn hạ với điều kiện là nó xuất hiện ở vị trí X

Mà nếu máy bay xuất hiện tại X thì bắn 2 quả tên lửa, xác suất bắn trúng máy bay của mỗi quả tên lửa là 0,8 và máy bay bị bắn hạ nếu nó trúng ít nhất 1 quả tên lửa

 là xác suất máy bay chiến đấu của đối phương bị bắn hạ với điều kiện là nó xuất hiện ở vị trí Y

Thay vào công thức ta có:

Vậy xác suất bắn hạ máy bay đối phương trong phương án tác chiến trên là 0,888

Bài 6.8: Có hai chuồng thỏ. Chuồng I có 5 con thỏ đen và 10 con thỏ trắng. Chuồng II có 7 con thỏ đen và 3 con thỏ trắng. Trước tiên, từ chuồng II lấy ra ngẫu nhiên 1 con thỏ rồi cho vào chuồng I. Sau đó, từ chuồng I lấy ra ngẫu nhiên 1 con thỏ. Tính xác suất để con thỏ được lấy ra là con thỏ trắng.

Lời giải:

Bài 6.9: Tại nhà máy X sản xuất linh kiện điện tử tỉ lệ sản phẩm đạt tiêu chuẩn là 80%. Trước khi xuất xưởng ra thị trường, các linh kiện điện tử đều phải qua khâu kiểm tra chất lượng để đóng dấu OTK. Vì sự kiểm tra không tuyệt đối hoàn hảo nên nếu một linh kiện điện tử đạt tiêu chuẩn thì nó có xác suất 0,99 được đóng dấu OTK; nếu một linh kiện điện tử không đạt tiêu chuẩn thì nó có xác suất 0,95 không được đóng dấu OTK. Chọn ngẫu nhiên một linh kiện điện tử của nhà máy X trên thị trường.

a) Tính xác suất để linh kiện điện tử đó được đóng dấu OTK.

b) Dùng sơ đồ hình cây, hãy mô tả cách tính xác suất để linh kiện điện tử được chọn không được đóng dấu OTK.

Lời giải:

Gọi A là biến cố:”Một linh kiện điện tử đạt tiêu chuẩn”

B là biến cố:”Một linh kiện được đóng dấu OTK”

Ta cần tính 

Theo công thức xác suất toàn phần, ta có:

Tỉ lệ sản phẩm đạt tiêu chuẩn là 80% 

 là xác suất một linh kiện được đóng dấu OTK với điều kiện nó đạt tiêu chuẩn 

là xác suất một linh kiện không được đóng dấu OTK với điều kiện nó không đạt tiêu chuẩn 

Thay vào công thức ta có:

Vậy xác suất để linh kiện điện tử đó được đóng dấu OTK là 0,802

b) Sơ đồ hình cây:

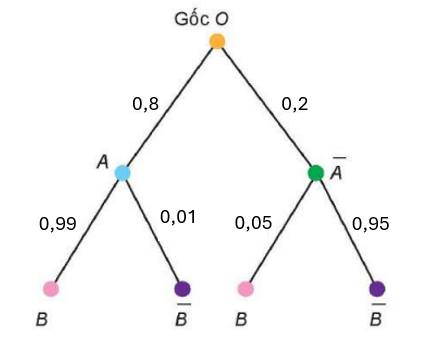
Có 2 nhánh cây đi tới  là  

Vậy xác suất để linh kiện điện tử được chọn không được đóng dấu OTK là:

Bài 6.10: Có hai đội thi đấu môn Bắn súng. Đội I có 5 vận động viên, đội II có 7 vận động viên. Xác suất đạt huy chương vàng của mỗi vận động viên đội I và đội II tương ứng là 0,65 và 0,55. Chọn ngẫu nhiên một vận động viên.

a) Tính xác suất để vận động viên này đạt huy chương vàng;

b) Giả sử vận động viên được chọn đạt huy chương vàng. Tính xác suất để vận động viên này thuộc đội I.

Lời giải:

a) Gọi A là biến cố: “VĐV được chọn thuộc đội I”;

B là biến cố: “VĐV được chọn thuộc đội II”;

E là biến cố: “VĐV được chọn đạt HCV”.

(Với VĐV: vận động viên, HCV: huy chương vàng).

Ta có B = $\overline{A}$.

Ta cần tính P(E). Theo công thức xác suất toàn phần, ta có

P(E) = P(A) ∙ P(E | A) + $P\left(\overline{A}\right)$.$P\left(E|\overline{A}\right)$.

Theo bài ra ta có: $P\left(A\right)=\frac{5}{12}$, $P\left(\overline{A}\right)=P\left(B\right)=\frac{7}{12}$.

P(E | A) là xác suất để VĐV thuộc đội I đoạt HCV. Theo bài ra ta có P(E | A) = 0,65.

$P\left(E|\overline{A}\right)$ là xác suất để VĐV thuộc đội II đoạt HCV. Theo bài ra ta có $P\left(E|\overline{A}\right)$ = 0,55.

Thay vào ta được P(E) = $\frac{5}{12}\cdot \mathrm{0,65}+\frac{7}{12}\cdot \mathrm{0,55}\approx$0,5917.

Vậy xác suất để vận động viên này đạt huy chương vàng là khoảng 0,5917.

b) Ta có xác suất để vận động viên được chọn thuộc đội I, biết rằng vận động viên này đạt huy chương vàng, chính là xác suất P(A | E).

Theo công thức Bayes và kết quả ở câu a) ta có

$P\left(A|E\right)=\frac{P\left(A\right)\cdot P\left(E|A\right)}{P\left(E\right)}\approx \frac{\frac{5}{12}\cdot \mathrm{0,65}}{\mathrm{0,5917}}\approx \mathrm{0,4577}$

Bài 6.11: Một bộ lọc được sử dụng để chặn thư rác trong các tài khoản thư điện tử. Tuy nhiên, vì bộ lọc không tuyệt đối hoàn hảo nên một thư rác bị chặn với xác suất 0,95 và một thư đúng (không phải là thư rác) bị chặn với xác suất 0,01. Thống kê cho thấy tỉ lệ thư rác là 3%.

a) Chọn ngẫu nhiên một thư bị chặn. Tính xác suất để đó là thư rác.

b) Chọn ngẫu nhiên một thư không bị chặn. Tính xác suất để đó là thư đúng.

c) Trong số các thư bị chặn, có bao nhiêu phần trăm là thư đúng? Trong số các thư không bị chặn, có bao nhiêu phần trăm là thư rác?

Lời giải: