Giải SGK Toán 12 Kết nối tri thức Bài 17: Phương trình mặt cầu

Mở đầu: Bằng ứng dụng Google Maps, thực hiện phép đo khoảng cách trên bề mặt Trái Đất từ vị trí 10°N, 15°E đến vị trí 80°N, 70°E ta sẽ được khoảng cách 8271,74 km (H.5.40). Cơ sở toán học cho việc thiết lập phần mềm tính công thức khoảng cách trên bề mặt Trái Đất là gì?

Lời giải:

- Ứng dụng Google Maps cho phép xác định khoảng cách giữa hai vị trí trên bề mặt Trái Đất khi biết vĩ độ và kinh độ của chúng. Khoảng cách giữa hai vị trí P và Q trên bề mặt trái đất là độ dài cung nhỏ PQ của đường tròn tâm O và đi qua hai điểm P, Q. Cung tròn nói trên là đường đi ngắn nhất trên bề mặt Trái Đất từ P đến Q.

1. Phương trình mặt cầu

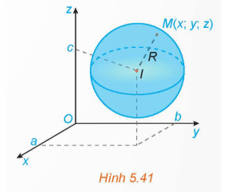
Hoạt động: Trong không gian Oxyz, cho mặt cầu (S) tâm I (a; b; c) bán kính R (H.5.41). Khi đó, một điểm M(x; y; z) thuộc mặt cầu (S) khi và chỉ khi tọa độ của nó thỏa mãn điều kiện gì?

Lời giải:

Điểm  thuộc mặt cầu  khi và chỉ khi: 

Hay 

Luyện tập 1: Trong không gian Oxyz, cho mặt cầu (S) có phương trình ${\left(x+2\right)}^2+y^2+{\left(z+\frac{1}{2}\right)}^2=\frac{9}{4}$.

a) Xác định tâm và bán kính của (S).

b) Hỏi điểm M(2; 0; 1) nằm trong, nằm ngoài hay thuộc mặt cầu (S).

Lời giải:

a) Mặt cầu (S) có tâm $I\left(-2;0;-\frac{1}{2}\right)$ và $R=\frac{3}{2}$

b) Có $IM=\sqrt{4^2+0^2+{\left(\frac{3}{2}\right)}^2}=\frac{\sqrt{73}}{2}>R$

Luyện tập 2: Trong không gian Oxyz, viết phương trình mặt cầu (S) trong các trường hợp sau:

a) Tâm là gốc tọa độ, bán kính R = 1.

b) Đường kính AB, với A(1; −1; 2), B(2; −3; −1).

Lời giải:

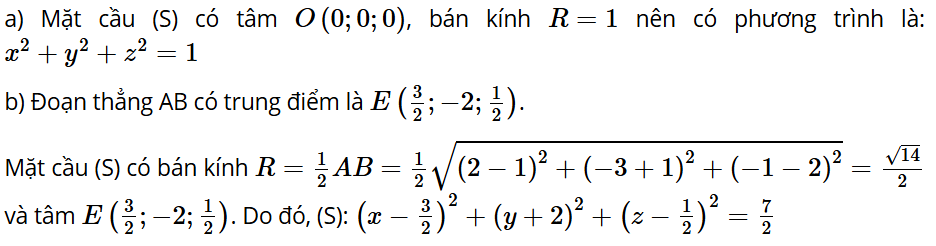
Luyện tập 3: Trong không gian Oxyz, cho (S) là tập hợp các điểm M(x; y; z) có tọa độ thỏa mãn phương trình (S): x2 + y2 + z2 – 4x + 6y – 12 = 0. Chứng minh rằng (S) là một mặt cầu. Xác định tâm và tính bán kính của mặt cầu đó.

Lời giải:

Ta viết lại phương trình đã cho dưới dạng:

Hay

Vậy  là mặt cầu có tâm  và có bán kính 

Luyện tập 4: Trong không gian Oxyz, cho mặt cầu (S) có phương trình $x^2+y^2+z^2+4x-5y+6z+\frac{25}{4}=0$. Xác định tâm, tính bán kính của (S).

Lời giải:

Từ phương trình trên ta có a = −2; $b=\frac{5}{2}$; c = −3 và $d=\frac{25}{4}$

Phương trình mặt cầu (S) có tâm $I\left(-2;\frac{5}{2};-3\right)$, $R=\sqrt{{\left(-2\right)}^2+{\left(\frac{5}{2}\right)}^2+{\left(-3\right)}^2-\frac{25}{4}}=\sqrt{13}.$

$2.\; Một\; số\; ứng\; dụng\; của\; phương\; trình\; mặt\; cầu\; trong\; thực\; tiễn$

Luyện tập 5: Tính khoảng cách trên mặt đất từ vị trí A là giao giữa kinh tuyến gốc với xích đạo đến vị trí B: 45°N, 30°E.

Lời giải:

Trải nghiệm: Trên Google Maps, thực hiện phép đo khoảng cách từ vị trí 0°N, 0°E đến vị trí 45°N, 30°E và so sánh với kết quả tính được ở luyện tập 5.

Lời giải:

Bước 1: Truy cập vào Google Maps.

Bước 2: Trên thanh tìm kiếm nhập 0°N, 0°E. Google Maps chuyển đến vị trí đó.

Bước 3. Nhấp vào vị trí đó và chuột phải chọn “Đo khoảng cách”.

Bước 4: Trên thanh tìm kiếm nhập 45°N, 30°E và nhấn enter. Google Maps đưa đến vị trí này.

Bước 5: Nhấp chuột vào vị trí này. Một đường thẳng hiện ra kèm thêm khoảng cách giữa hai vị trí này.

Kết quả như hình vẽ sau:

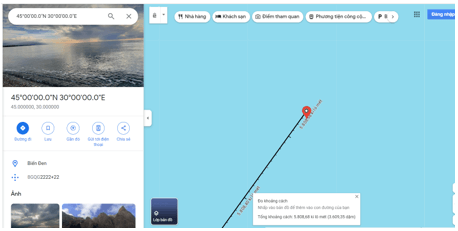
Từ đây ta thấy kết quả đo tương đối chính xác với kết quả tính ở luyện tập 5.

Bài tập

Bài 5.25: Trong không gian Oxyz, cho mặt cầu (S) có phương trình ${\left(x-\frac{1}{2}\right)}^2+{\left(y+1\right)}^2+z^2=9$. Xác định tâm và bán kính của (S).

Lời giải:

Bài 5.26: Trong không gian Oxyz, viết phương trình của mặt cầu (S) có tâm I(−2; 0; 5) và bán kính R = 2.

Lời giải:

- Mặt cầu (S) có tâm I(−2; 0; 5) và bán kính R = 2 có phương trình là: (x + 2)2 + y2 + (z – 5)2 = 4.

Bài 5.27: Trong không gian Oxyz, viết phương trình của mặt cầu (S) có tâm I(0; 3; −1) và có bán kính bằng khoảng cách từ I đến mặt phẳng (P): 3x + 2y – z = 0.

Lời giải:

Ta có $R=d\left(I,\left(P\right)\right)=\frac{\left|}{3.0+2.3+1}=\frac{7}{\sqrt{14}}$

Mặt cầu (S) có tâm I(0; 3; −1) và $R=\frac{7}{\sqrt{14}}$ có phương trình là:

$x^2+{\left(y-3\right)}^2+{\left(z+1\right)}^2=\frac{49}{14}$

Bài 5.28: Trong không gian Oxyz, cho mặt cầu (S): x2 + y2 + z2 + 2x – 2y + 8z – 18 = 0. Xác định tâm, tính bán kính của (S).

Lời giải:

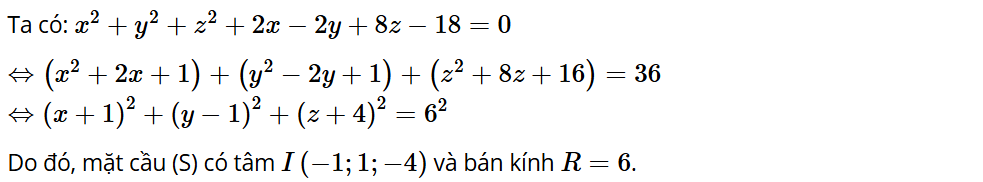
Bài 5.29: Trong không gian Oxyz, phương trình nào trong các phương trình sau là phương trình mặt cầu? Xác định tâm và tính bán kính của mặt cầu đó.

a) x2 + y2 + z2 – 2x – 5z + 30 = 0;

b) x2 + y2 + z2 – 4x + 2y – 2z = 0;

c) x3 + y3 + z3 – 2x + 6y – 9z – 10 = 0;

d) x2 + y2 + z2 + 5 = 0.

Lời giải:

a) Phương trình đã cho tương ứng với . Trong trường hợp này, . Do đó phương trình đã cho không phải là phương trình của một mặt cầu. 

b) Phương trình đã cho tương ứng với . Trong trường hợp này, . Do đó phương trình đã cho là phương trình mặt cầu có tâm  và bán kính . 

c) Phương trình đã cho có bậc của x, y, z là 3 nên đây không phải là phương trình của một mặt cầu.

d) Phương trình đã cho tương ứng với . Trong trường hợp này, . Do đó phương trình đã cho không phải là phương trình của một mặt cầu.

Bài 5.30: Trong không gian Oxyz, một thiết bị phát sóng đặt tại vị trí A(2; 0; 0). Vùng phủ sóng của thiết bị có bán kính bằng 1.Hỏi vị trí M(2; 1; 1) có thuộc vùng phủ sóng của thiết bị nói trên hay không?

Lời giải:

Ta có $AM=\sqrt{{\left(2-2\right)}^2+1^2+1^2}=\sqrt{2}>1$

Do đó vị trí M(2; 1; 1) không thuộc vùng phủ sóng của thiết bị nói trên.