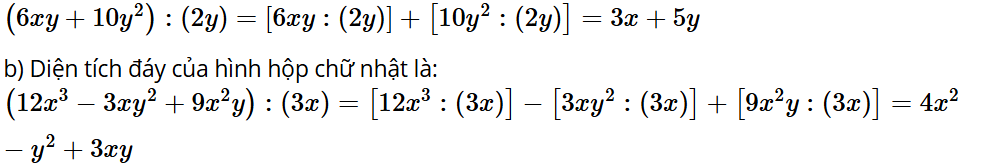Giải SGK Toán 8 Chân trời sáng tạo Bài 2: Các phép toán với đa thức nhiều biến

Khởi động: Trên một đoạn sông thẳng, xuất phát cùng một lúc từ một bến thuyền, thuyền đi xuôi dòng với vận tốc (v + 3) km/h, ca nô đi ngược dòng với tốc độ (2v – 3) km/h. Làm thế nào để tìm được quãng đường của mỗi phương tiện và khoảng cách giữa chúng sau khoảng thời gian t giờ kể từ khi rời bến?

Lời giải:

Sau khoảng thời gian t giờ, thuyền đi xuôi dòng được quãng đường là:

s = (v + 3).t (km).

Sau khoảng thời gian t giờ, ca nô đi ngược dòng được quãng đường là:

s’ = (2v – 3).t (km).

Khoảng cách giữa hai phương tiện sau khoảng thời gian t giờ là:

d = s + s’ = (v + 3).t + (2v – 3).t

= vt + 3t + 2vt – 3t

= (vt + 2vt) + (3t – 3t)

= 3vt (km).

1. Cộng, trừ đa thức

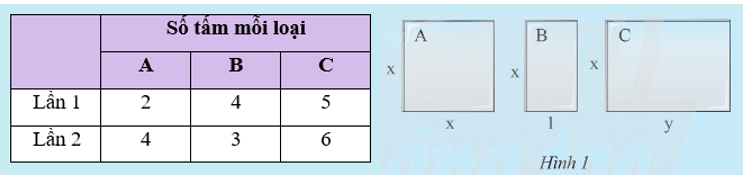
Khám phá 1: Tại một công trình xây dựng, người ta dùng ba loại tấm kính chống nắng A, B và C với kích thước như Hình 1 (tính bằng m). Giá tiền các tấm kính được tính theo diện tích với đơn giá a đồng/m2. Tại đây có hai lần nhập vật liệu như bảng sau:

a) Tính tổng số tiền mua kính của cả hai lần.

b) Số tiền lần 2 nhiều hơn lần 1 bao nhiêu?

Lời giải:

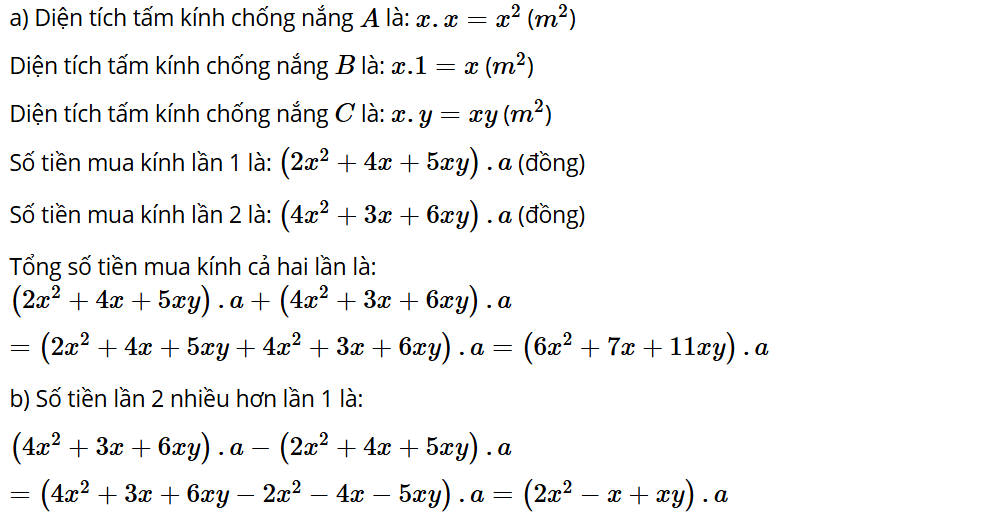
Thực hành 1: Cho hai đa thức M = 1 + 3xy – 2x2y2 và N = x – xy + 2x2y2. Tính M + N và M – N.

Lời giải:

M+N=(1+3xy−2x2y2)+(x−xy+2x2y2)

=1+3xy−2x2y2+x−xy+2x2y2

=1+(3xy−xy)+(2x2y2−2x2y2)+x

=1+2xy+x

M−N=(1+3xy−2x2y2)−(x−xy+2x2y2)

=1+3xy−2x2y2−x+xy−2x2y2

=1+(3xy+xy)−(2x2y2+2x2y2)−x=1+4xy−4x2y2−x

2. Nhân hai đa thức

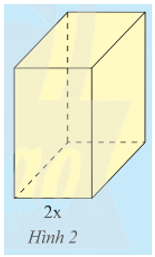
Khám phá 2: Hình hộp chữ nhật A có chiều rộng 2x, chiều dài và chiều cao đều gấp k lần chiều rộng (Hình 2)

a) Tính diện tích đáy của A.

b) Tính thể tích của A.

Lời giải:

a) Chiều dài của hình hộp chữ nhật A là: k.2x = 2kx.

Diện tích đáy của hình hộp chữ nhật A là:

Sđáy = (2x).(2kx) = (2.2).k.(x.x) = 4kx2 (đơn vị diện tích).

Vậy diện tích đáy của hình hộp chữ nhật A là 4kx2 (đơn vị diện tích).

b) Chiều cao của hình hộp chữ nhật A là: k.2x = 2kx.

Thể tích của hình hộp chữ nhật A là:

V = Sđáy.h = (4kx2).(2kx) = (4.2).(k.k).(x2.x) = 8k2x3 (đơn vị thể tích).

Vậy thể tích của hình hộp chữ nhật A là 8k2x3 (đơn vị thể tích).

Thực hành 2: Thực hiện các phép nhân đơn thức sau:

a) (4x3).(–6x3y);

b) (–2y).(–5xy2);

c) (–2a)3.(2ab)2.

Lời giải:

a) (4x3)×(−6x3y)=[4×(−6)]×(x3×x3)×y=−24x6y

b) (−2y)×(−5xy2)=[(−2)×(−5)]×(y×y2)×x=10xy3

c) (−2z)3×(2ab)2=[(−2)3×22]×a3×a2×b2=−32a5b2

Khám phá 3: 

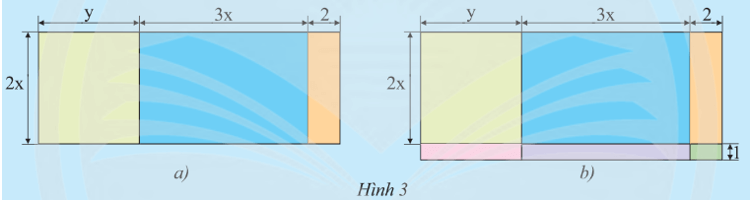
a) Hình 3a là bản vẽ sơ lược sàn của một căn hộ (các kích thước tính theo m). Tính diện tích sàn này bằng những cách khác nhau.

b) Nếu vẽ cả ban công thì được sơ đồ như Hình 3b. Hãy tính tổng diện tích của sàn bao gồm cả ban công.

Lời giải:

a) Cách 1: Diện tích sàn là:

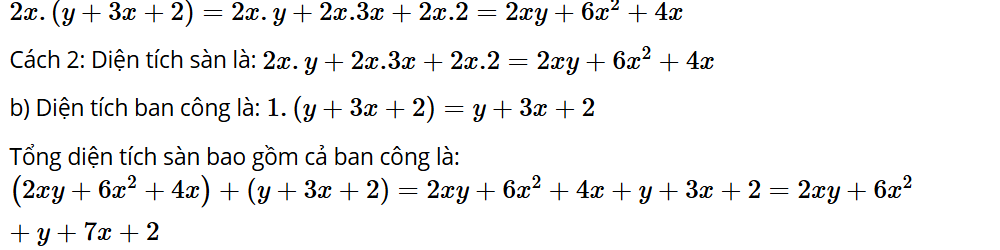
Thực hành 3: Viết các biểu thức sau thành đa thức:

a) (–5a4)(a2b – ab2);

b) (x + 2y)(xy2 – 2y3).

Lời giải:

a) (–5a4)(a2b – ab2)

= (–5a4).(a2b) – (–5a4).(ab2)

= –5.(a4.a2).b + 5.(a4.a).b2

= –5a6b + 5a5b2.

b) (x + 2y)(xy2 – 2y3)

= x.(xy2 – 2y3) + 2y.(xy2 – 2y3)

= x.xy2 – x.2y3 + 2y.xy2 – 2y.2y3

= x2y2 – 2xy3 + 2xy3 – 4y4

= x2y2 + (– 2xy3 + 2xy3) – 4y4

= x2y2 – 4y4.

Vận dụng 1: Viết biểu thức tính khoảng cách giữa hai phương tiện trong tình huống ở Hoạt động khởi động (trang 12).

Lời giải:

Quãng đường thuyền đi được sau t giờ: (v+3)t = vt + 3t (km)

Quãng đường ca nô đi được sau t giờ: (2v-3)t = 2vt - 3t (km)

Khoảng cách hai phương tiện sau t giờ: vt +3t + 2vt - 3t = 3vt (km

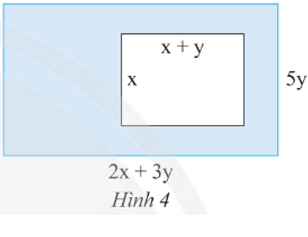
Vận dụng 2: Tính diện tích phần tô màu trong Hình 4.

Lời giải:

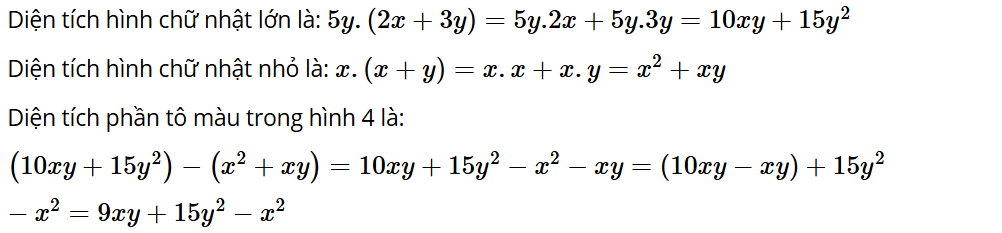
3. Chia đa thức cho đơn thức

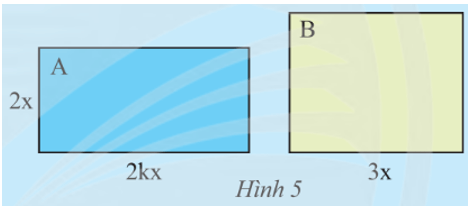
Khám phá 4: Hình chữ nhật A có chiều rộng 2x (cm), chiều dài gấp k (k > 1) lần chiều rộng. Hình chữ nhật B có chiều dài 3x (cm). Muốn hai hình chữ nhật này có diện tích bằng nhau thì B phải có chiều rộng bằng bao nhiêu?

Lời giải:

Diện tích hình chữ nhật A là: SA = 2x.2kx = 4kx2 (cm2).

Gọi chiều rộng của hình chữ nhật B là R (cm).

Khi đó diện tích của hình chữ nhật B là: SB = R.3x (cm2).

Để hai hình chữ nhật này có diện tích bằng nhau thì SA = SB

Do đó 4kx2 = R.3x

Suy ra R = (4kx2) : (3x)

           R = (4 : 3).k.(x2 : x) = $\frac{4}{3}$kx (cm).

Vậy để hai hình chữ nhật này có diện tích bằng nhau thì chiều rộng của hình chữ nhật B là $\frac{4}{3}$kx cm.

Thực hành 4: Thực hiện phép chia 8x4y5z3 cho 2x3y4z

Lời giải:

(8x4y5z3):(2x3y4z)=(8:2)(x4:x3)(y5:y4)(z3:z)=4xyz2

Vận dụng 3: Tính diện tích đáy của hình hộp chữ nhật có thể tích V = 12x2y và chiều cao bằng 3y.

Lời giải:

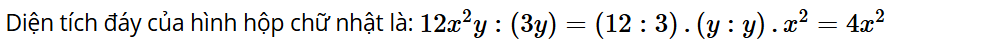
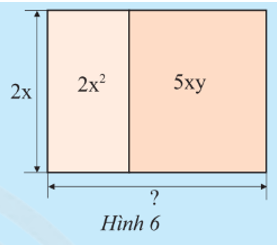
Khám phá 5: Một bức tường được trang trí bởi hai tấm giấy dán có cùng chiều cao 2x (m) và có diện tích lần lượt là 2x2 (m2) và 5xy (m2).

a) Tính chiều rộng của mỗi tấm giấy, từ đó tìm chiều rộng của bức tường.

b) Từ kết quả trên, có thể biết được kết quả của phép chia đa thức A = 2x2 + 5xy cho đơn thức B = 2x không? Hãy giải thích.

Lời giải:

a) Chiều rộng của tấm giấy dán thứ nhất là:

(2x2) : (2x) = (2 : 2).(x2 : x) = x (m).

Chiều rộng của tấm giấy dán thứ hai là:

(5xy) : (2x) = (5 : 2).(x : x).y = $\frac{5}{2}$y (m).

Chiều rộng của bức tường là: $\frac{5}{2}$(m).

b) Diện tích bức tường chính là tổng diện tích hai tấm giấy dán, và bằng:

2x2 + 5xy (m2).

Bức tường có chiều cao là 2x (m), do đó chiều rộng của bức tường là kết quả của phép chia đa thức A = 2x2 + 5xy cho đơn thức B = 2x.

Mà theo câu a, chiều rộng của bức tường là: $\frac{5}{2}$(m).

Vậy từ kết quả ở câu a, ta có thể biết được kết quả của phép chia đa thức A = 2x2 + 5xy cho đơn thức B = 2x là bằng $\frac{5}{2}$.

Thực hành 5: Thực hiện các phép chia:

a) (5ab – 2a2) : a;

b) (6x2y2 – xy2 + 3x2y) : (–3xy).

Lời giải:

a) (5ab−2a2):a=(5ab:a)−(2a2:a)=5b−2a

b) (6x2y2−xy2+3x2y):(−3xy)

=[6x2y2:(−3xy)]−[xy2:(−3xy)]+[3x2y:(−3xy)]

=−2xy+13y−x

Vận dụng 4: Tính chiều cao của hình hộp chữ nhật có thể tích V = 6x2y – 8xy2 và diện tích đáy S = 2xy.

Lời giải:

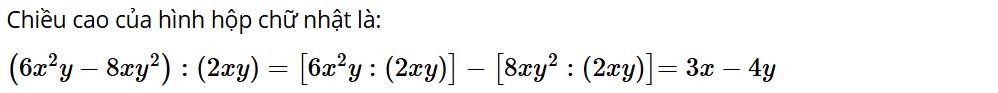
Bài tập

Bài tập 1: Tính:

a) x + 2y + (x – y);

b) 2x – y – (3x – 5y);

c) 3x2 – 4y2 + 6xy + 7 + (–x2 + y2 – 8xy + 9x + 1);

d) 4x2y – 2xy2 + 8 – (3x2y + 9xy2 – 12xy + 6).

Lời giải:

a) x + 2y + (x – y)

= x + 2y + x – y

= (x + x) + (2y – y)

= 2x + y.

b) 2x – y – (3x – 5y)

= 2x – y – 3x + 5y

= (2x – 3x) + (–y + 5y)

= –x + 4y.

c) 3x2 – 4y2 + 6xy + 7 + (–x2 + y2 – 8xy + 9x + 1)

= 3x2 – 4y2 + 6xy + 7 – x2 + y2 – 8xy + 9x + 1

= (3x2 – x2) + (– 4y2 + y2) + (6xy – 8xy) + 9x + (7 + 1)

= 2x2 – 3y2 – 2xy + 9x + 8 .

d) 4x2y – 2xy2 + 8 – (3x2y + 9xy2 – 12xy + 6).

= 4x2y – 2xy2 + 8 – 3x2y – 9xy2 + 12xy – 6

= (4x2y – 3x2y) + (– 2xy2 – 9xy2) + 12xy + (8 – 6)

= x2y – 11xy2 + 12xy + 2 .

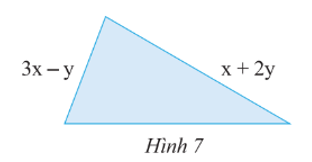
Bài tập 2: Tìm độ dài cạnh còn thiếu của tam giác ở Hình 7, biết rằng tam giác có chu vi bằng 7x + 5y.

Lời giải:

Độ dài cạnh còn lại là: 7x + 5y - (3x - y + x + 2y) = 7x + 5y - 3x + y - x - 2y = 3x + 4y

Bài tập 3: Thực hiện phép nhân:

a) 3x(2xy – 5x2y);

b) 2x2y(xy – 4xy2 + 7y);

c) $\left(-\frac{2}{3}x{y}^2+6y{z}^2\right).\left(-\frac{1}{2}xy\right)$.

Lời giải:

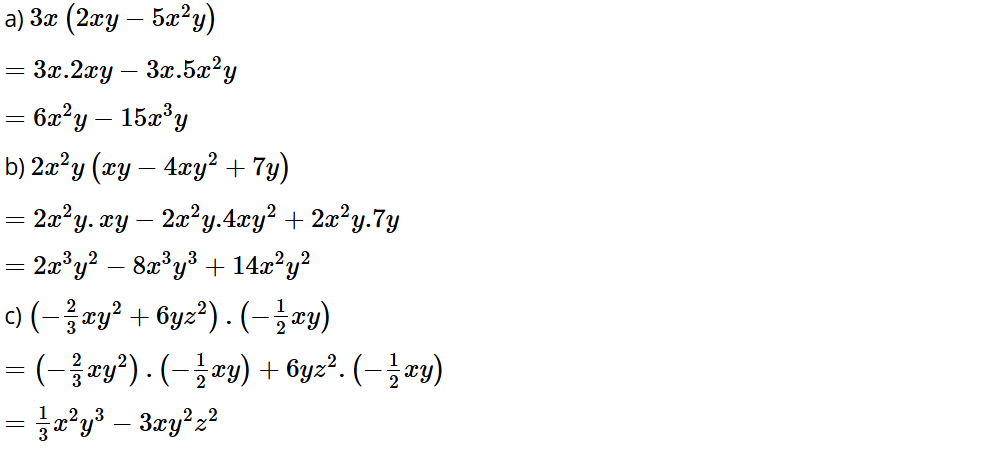
Bài tập 4: Thực hiện phép nhân:

a) (x – y)(x – 5y);

b) (2x + y)(4x2 – 2xy + y2).

Lời giải:

a) (x – y)(x – 5y)

= x.(x – 5y) – y.(x – 5y)

= x.x – x.5y – y.x + y.5y

= x2 – 5xy – xy + 5y2

= x2 – 6xy + 5y2.

b) (2x + y)(4x2 – 2xy + y2)

= 2x.(4x2 – 2xy + y2) + y.(4x2 – 2xy + y2)

= 2x.4x2 – 2x.2xy + 2x.y2 + y.4x2 – y.2xy + y.y2

= 8x3 – 4x2y + 2xy2 + 4x2y – 2xy2 + y3

= 8x3 + (– 4x2y + 4x2y) + (2xy2 – 2xy2) + y3

= 8x3 + y3.

Bài tập 5: Thực hiện phép chia:

a) 20x3y5 : (5x2y2);

b) 18x3y5 : [3(–x)3y2].

Lời giải:

a) 20x3y5:(5x2y2)=4xy3

b) 18x3y5:[3(−x)3y2]=−6y3

Bài tập 6: Thực hiện phép chia:

a) (4x3y2 – 8x2y + 10xy) : (2xy);

b) (7x4y2 – 2x2y2 – 5x3y4) : (3x2y).

Lời giải:

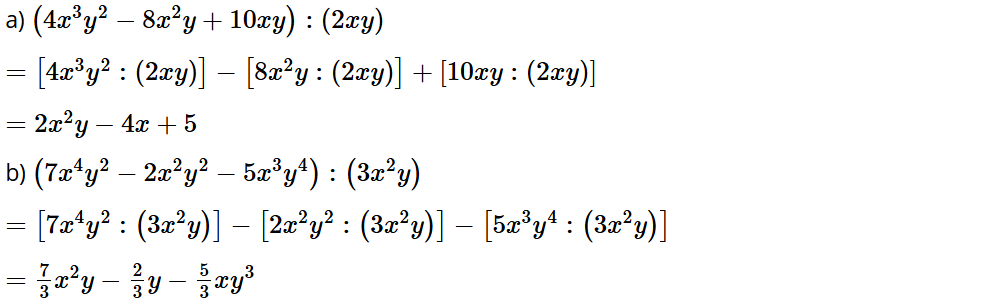
Bài tập 7: Tính giá trị của biểu thức:

a) 3x2y – (3xy – 6x2y) + (5xy – 9x2y) tại x = $\frac{2}{3}$, y = - $\frac{3}{4}$;

b) x(x – 2y) – y(y2 – 2x) tại x = 5, y = 3.

Lời giải:

a) Thu gọn biểu thức:

3x2y – (3xy – 6x2y) + (5xy – 9x2y)

= 3x2y – 3xy + 6x2y + 5xy – 9x2y

= (3x2y + 6x2y – 9x2y) + (– 3xy + 5xy)

= 2xy

 Thay x = $\frac{2}{3}$ và y = - $\frac{3}{4}$ vào biểu thức đã thu gọn ta có:

$2.\frac{2}{3}.\left(-\frac{3}{4}\right)=-1$.

b) Thu gọn biểu thức:

x(x – 2y) – y(y2 – 2x)

= x.x – x.2y – y.y2 + y.2x

= x2 – 2xy – y3 + 2xy

= x2 + (– 2xy + 2xy) – y3

= x2 – y3

Thay x = 5 và y = 3 vào biểu thức đã thu gọn ta có:

52 – 33 = 25 – 27 = –2.

Bài tập 1: Trên một dòng sông, để đi được 10 km, một chiếc xuồng tiêu tốn a lít dầu khi xuôi dòng và tiêu tốn (a + 2) lít dầu khi ngược dòng. Viết biểu thức biểu thị số lít dầu mà xuồng tiêu tốn để đi từ bến A ngược dòng đến bến B, rồi quay lại bến A. Biết khoảng cách giữa hai bến là b km

Lời giải:

Để đi được 1 km khi ngược dòng tốn 110(a+2) lít dầu và khi xuôi dòng tốn a10

Ta có: Biểu thức biểu thị số lít dầu mà xuồng tiêu tốn để đi từ bến A ngược dòng đến bến B, rồi quay lại bến A là:

[110(a+2)]b+(a10)b=ab10+2b10+ab10=ab5+b5 (lít dầu)

Bài tập 9:

a) Tính chiều dài của hình chữ nhật có diện tích bằng 6xy + 10y2 và chiều rộng bằng 2y.

b) Tính diện tích đáy của hình hộp chữ nhật có thể tích bằng 12x3 – 3xy2 + 9x2y và chiều cao bằng 3x.

Lời giải:

a) Chiều dài hình chữ nhật là: