Giải SGK Toán 8 Chân trời sáng tạo Bài 2: Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều

Khởi động: 

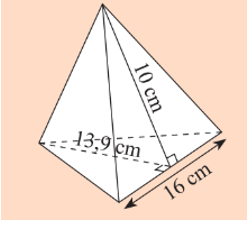
a) Bạn Mai cần dán giấy bóng kính màu xung quanh một chiếc lồng đèn hình chóp tam giác đều với kích thước như hình bên. Hỏi diện tích giấy mà Mai cần là bao nhiêu?

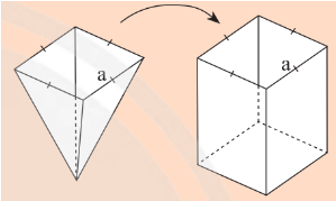
b) Bạn Hùng dùng một cái gàu hình chóp tứ giác đều để múc nước đổ vào một thùng chứa hình lăng trụ có cùng diện tích đáy và chiều cao như hình bên. Hãy dự đoán xem bạn Hùng phải đổ bao nhiêu gàu thì nước đầy thùng.

Lời giải:

a) Diện tích giấy bạn Mai cần dán là: 12×16×13.9+3×12×16×10=351.2(cm2)

b) Gọi chiều cao của cái gàu là h

Thể tích của gàu nước là: V1=13×Sđáy×h

Thể tích của thành nước là: V2=Sđáy×h

Bạn Hùng phải đổ số gàu nước là: V2V1=3 

1. Diện tích xung quanh của hình chóp tam giác đều và hình chóp tứ giác đều

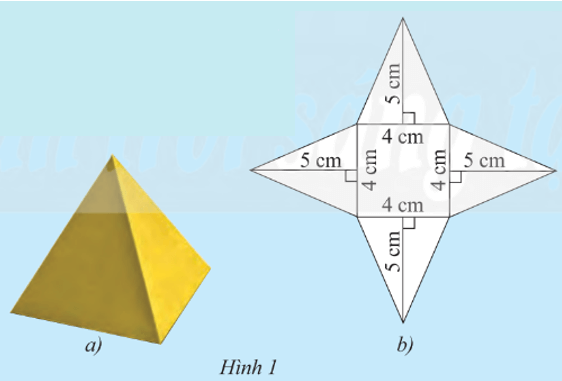
Khám phá 1: Nam làm một chiếc hộp hình chóp tứ giác đều như Hình 1a, sau đó Nam trải các mặt của chiếc hộp với các số đo đã cho như Hình 1b. Hãy cho biết:

a) Hình này có bao nhiêu mặt bên.

b) Diện tích của mỗi mặt bên.

c) Diện tích của tất cả mặt các bên.

d) Diện tích đáy của hình này.

Lời giải:

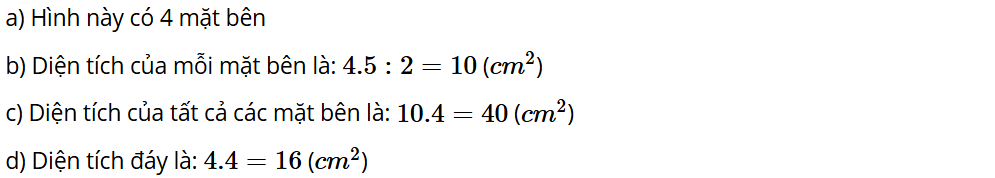
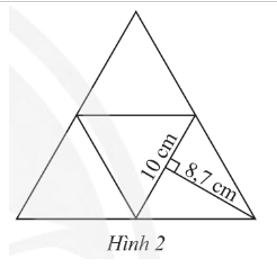
Thực hành 1: Một tấm bìa (Hình 2) gấp thành hình chóp tam giác đều với các mặt đều là hình tam giác đều. Với số đo trên hình vẽ, hãy tính diện tích xung quanh và diện tích toàn phần của hình này.

Lời giải:

Diện tích xung quanh của hình chóp: Sxq=3×12×10×8.7=130.5(cm2)

Diện tích toàn phần của hình chóp: Stp=Sxq+Sđáy=130.5+12×10×8.7=174(cm2)

2. Thể tích của hình chóp tam giác đều và hình chóp tứ giác đều

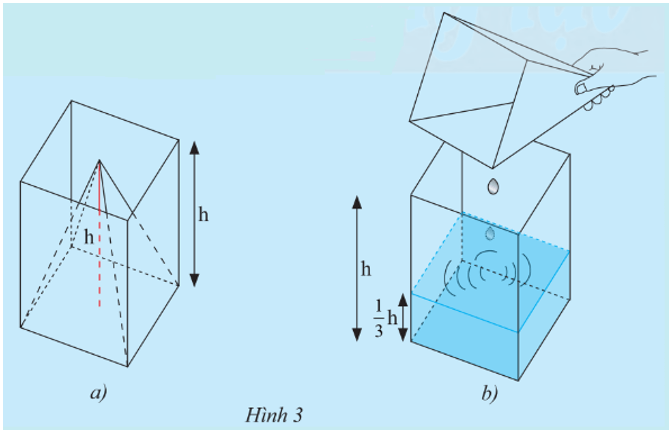
Khám phá 2: Bạn Hùng có một cái gàu có dạng hình chóp tứ giác đều và một cái thùng (không chứa nước) có dạng hình lăng trụ đứng. Hai vật này có cùng diện tích đáy và chiều cao (Hình 3a). Hùng múc đầy một gàu nước và đổ vào thùng thì thấy chiều cao của cột nước bằng 

$\frac{1}{3}$ chiều cao của thùng (Hình 3b). Gọi Sđáy­ là diện tích đáy và h là chiều cao của cái gàu.

a) Tính thể tích V của phần nước đổ vào theo Sđáy và h.

b) Từ câu a), hãy dự đoán thể tích của cái gàu.

Lời giải:

a) Thể tích của phần nước đổ vào là: $V=S_{đáy}.\frac{1}{3}h=\frac{1}{3}.S_{đáy}.h$.

b) Dự đoán: Thể tích của cái gàu là: $V=\frac{1}{3}.S_{đáy}.h$.

Thực hành 2: Tính thể tích của một chiếc hộp bánh ít có dạng hình chóp tứ giác đều, có độ dài cạnh đáy là 3 cm và chiều cao là 2,5 cm.

Lời giải:

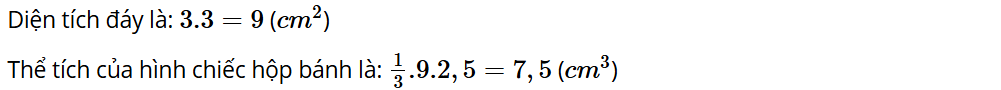
Thực hành 3: Hãy giải bài toán ở phần Hoạt động khởi động (trang 49).

Lời giải:

a) Diện tích giấy bạn Mai cần dán là: 12×16×13.9+3×12×16×10=351.2(cm2)

b) Gọi chiều cao của cái gàu là h

Thể tích của gàu nước là: V1=13×Sđáy×h

Thể tích của thành nước là: V2=Sđáy×h

Bạn Hùng phải đổ số gàu nước là: V2V1=3 

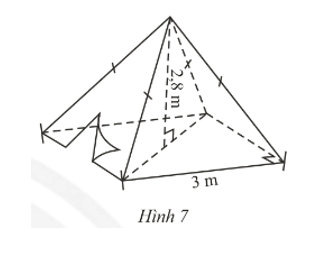
Vận dụng 1: Một chiếc lều có dạng hình chóp tứ giác đều ở trại hè của học sinh có kích thước như Hình 7.

a) Tính thể tích không khí trong chiếc lều.

b) Tính diện tích vải lều (không tính các mép dán), biết chiều cao của mặt bên xuất phát từ đỉnh của chiếc lều là 3,18 m và lều này không có đáy.

Lời giải:

a) Thể tích không khí trong chiếc lều là:

$V=\frac{1}{3}.S_{đáy}.h=\frac{1}{3}{.3}^2.2,8=8,4$ (m3).

Vậy thể tích không khí trong chiếc lều là 8,4 m3.

b) Diện tích vải lều (diện tích xung quanh của chiếc lều) không tính các mép dán là:

$S_{xq}=4.\frac{1}{2}.3,18.3=19,08$ (m2).

Vậy diện tích vải lều không tính các mép dán là 19,08 m2.

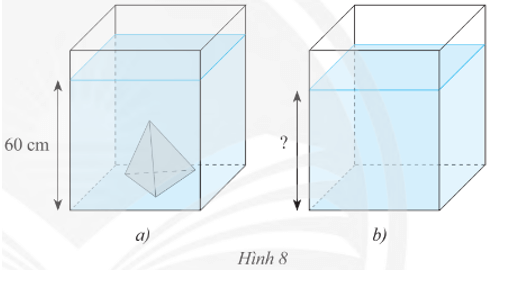
Vận dụng 2: Một bể kính hình hộp chữ nhật có hai cạnh đáy là 60 cm và 30 cm. Trong bể có một khối đá hình chóp tam giác đều với diện tích đáy là 270 cm2, chiều cao 30 cm. Người ta đổ nước vào bể sao cho nước ngập khối đá và đo được mực nước là 60 cm. Khi lấy khối đá ra thì mực nước của bể là bao nhiêu? Biết rằng bề dày của bể và thành bể không đáng kể.

Lời giải:

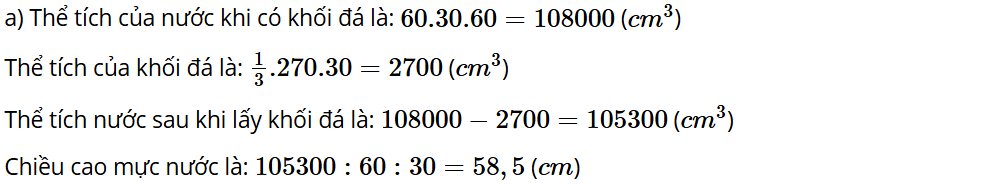
Bài tập

Bài tập 1: 

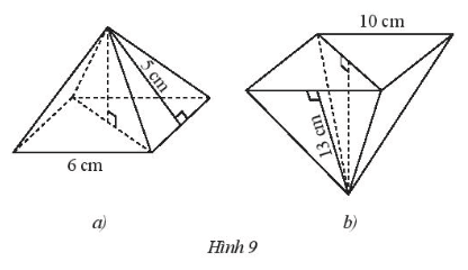
a) Tính diện tích xung quanh của mỗi hình chóp tứ giác đều dưới đây.

b) Cho biết chiều cao của hình chóp tứ giác đều trong Hình 9a và Hình 9b lần lượt là 4 cm và 12 cm. Tính thể tích của mỗi hình.

Lời giải:

a)

Diện tích xung quanh của hình 9a: 4×12×5×6=60(cm2)

Diện tích xung quanh của hình 9b: 4×12×13×10=260(cm2)

b) Thể tích hình 9a là: 13×62×4=72(cm3)

Thể tích hình 9b là: 13×102×12=400(cm3)

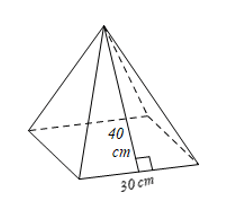
Bài tập 2: Nhân dịp Tết Trung thu, Nam dự định làm một chiếc lồng đèn hình chóp tứ giác đều có độ dài cạnh đáy và đường cao của mặt bên tương ứng với cạnh đáy lần lượt là 30 cm và 40 cm. Em hãy giúp Nam tính xem phải cần bao nhiêu mét vuông giấy vừa đủ để dán tất cả các mặt của chiếc lồng đèn. Biết rằng nếp gấp không đáng kể.

Lời giải:

Diện tích giấy dán bốn mặt bên (diện tích xung quanh) của chiếc lồng đèn hình chóp tứ giác đều là:

$S_{xq}=4.\frac{1}{2}\mathrm{.40.30}=2400$ (cm2).

Diện tích giấy dán mặt đáy của chiếc lồng đèn hình chóp tứ giác đều là:

Sđáy = 302 = 600 (cm2).

Diện tích giấy dán tất cả các mặt (diện tích toàn phần) của chiếc lồng đèn là:

Stp = S­xq + Sđáy = 2 400 + 600 = 3 000 (cm2) = 0,33 m2.

Vậy cần 0,33 mét vuông giấy vừa đủ để dán tất cả các mặt của chiếc lồng đèn.

Bài tập 3:

a) Tính diện tích xung quanh của hình chóp tam giác đều có độ dài cạnh đáy là 10 cm, chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tam giác đều là 12 cm.

b) Tính diện tích toàn phần và thể tích của hình chóp tứ giác đều có độ dài cạnh đáy là 72 dm, chiều cao là 68,1 dm, chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tứ giác đều là 77 dm.

Lời giải:

Bài tập 4: Bảo tàng Louvre (Pháp) có một kim tự tháp hình chóp tứ giác đều bằng kính (gọi là kim tự tháp Louvre) có chiều cao 21,3 m và cạnh đáy 34 m. Tính thể tích của kim tự tháp này.

(Nguồn: https://www.pariscityvision.com/en/paris/museums)

Lời giải:

Thể tích của kim tự tháp: 13×342×21.3=8207.6(m3)