Giải SGK Toán 8 Chân trời sáng tạo Bài 7: Nhân, chia phân thức

Khởi động: Ô tô A tiêu tốn a lít xăng để đi hết quãng đường x (km). Ô tô B tiêu tốn b lít xăng để đi hết quãng đường y (km). Để đi được 100 km,

a) Mỗi ô tô tiêu tốn bao nhiêu lít xăng?

b) Ô tô A tiêu tốn lượng xăng gấp bao nhiêu lần ô tô B?

Lời giải:

Để đi được 1 km thì ô tô A tiêu tốn lượng xăng là: $\frac{a}{x}$ (lít).

Để đi được 1 km thì ô tô B tiêu tốn lượng xăng là: $\frac{b}{y}$ (lít).

a) Để đi được 100 km thì ô tô A tiêu tốn lượng xăng là: 100.$\frac{a}{x}$ (lít).

Để đi được 100 km thì ô tô B tiêu tốn lượng xăng là: 100.$\frac{b}{y}$ (lít).

b) Để đi được 100 km, ô tô A tiêu tốn lượng xăng gấp số lần ô tô B là:

$\frac{100a}{x}:\frac{100b}{y}$ = $\frac{100a}{x}.\frac{y}{100b}$ = $\frac{ay}{bx}$ (lần).

Vậy ô tô A tốn lượng xăng gấp $\frac{ay}{bx}$ lần ô tô B.

1. Nhân hai phân thức

Khám phá 1: Một tấm bạt lớn hình chữ nhật có chiều dài a (m), chiều rộng b (m) được ghép bởi các tấm bạt bé hình chữ nhật có chiều dài và chiều rộng đều bằng $\frac{1}{\mathrm{k}}$ chiều dài, chiều rộng của tấm bạt lớn.

Tính diện tích của mỗi tấm bạt bé theo a, b và k

Lời giải:

Chiều dài của tấm bạt bé là: $\frac{1}{k}.a=\frac{a}{k}$ (m).

Chiều rộng của tấm bạt bé là: $\frac{1}{k}.b=\frac{b}{k}$ (m).

Diện tích của mỗi tấm bạt bé là: $\frac{a}{k}.\frac{b}{k}=\frac{ab}{k^2}$ (m2).

Vậy diện tích của mỗi tấm bạt bé theo a, b và k là $\frac{ab}{k^2}$ (m2).

Thực hành 1: Tính:

a) $\frac{3a^2}{10b^3}.\frac{15b}{9a^4}$

b) $\frac{x-3}{x^2}.\frac{4x}{x^2-9}$

c) $\frac{a^2-6a+9}{a^2+3a}.\frac{2a+6}{a-3}$

d) $\frac{x+1}{x}.\left(x+\frac{2-x^2}{x^2-1}\right)$

Lời giải:

a) 3a210b3×15b9a4=3a2×15b10b3×9a4=45a2b90a4b3=12a2b2

b) x−3x2×4xx2−9=(x−3)4xx2(x2−9)=4x(x−3)x2(x−3)(x+3)=4xx2(x+3)=4x(x+3)

c) a2−6a+9a2+3a×2a+6a−3=(a−3)2×2(a+3)a(a+3)(a−3)=2(a−3)a

d) x+1x×(x+2−x2x2−1)=x+1x×x+x+1x×2−x2x2−1=x+1+2−x2x(x−1)

=(x2−1)x+2−x2x(x−1)=x3−x+2−x2x(x−1)

2. Chia hai phân thức

Khám phá 2: Máy A xát được x tấn gạo trong a giờ; máy B xát được y tấn gạo trong b giờ.

a) Viết các biểu thức biểu thị số tấn gạo mỗi máy xát được trong 1 giờ (gọi là công suất của máy).

b) Công suất của máy A gấp bao nhiêu lần máy B? Viết biểu thức biểu thị số lần này.

c) Tính giá trị của biểu thức ở câu b) khi x = 3, a = 5, y = 2, b = 4

Lời giải:

Thực hành 2: Thực hiện các phép tính sau:

a) $\frac{x^2-9}{x-2}:\frac{x-3}{x}$

b) $\frac{x}{z^2}.\frac{xz}{y^3}:\frac{x^3}{yz}$

c) $\frac{2}{x}-\frac{2}{x}:\frac{1}{x}+\frac{4}{x}.\frac{x^2}{2}$

Lời giải:

a) $\frac{x^2-9}{x-2}:\frac{x-3}{x}=\frac{\left(x+3\right)\left(x-3\right)}{x-2}.\frac{x}{x-3}$

$=\frac{\left(x+3\right)\left(x-3\right).x}{\left(x-2\right).\left(x-3\right)}=\frac{x\left(x+3\right)}{x-2}$

b) $\frac{x}{z^2}.\frac{xz}{y^3}:\frac{x^3}{yz}=\left(\frac{x}{z^2}.\frac{xz}{y^3}\right):\frac{x^3}{yz}=\frac{x^{2}z}{y^3{z}^2}.\frac{yz}{x^3}=\frac{1}{x{y}^2}$

c) $\frac{2}{x}-\frac{2}{x}:\frac{1}{x}+\frac{4}{x}.\frac{x^2}{2}=\frac{2}{x}-\frac{2}{x}.\frac{x}{1}+2x$

$=\frac{2}{x}-2+2x=\frac{2-2x+2x^2}{x}$

Vận dụng: Đường sắt và đường bộ từ thành phố A đến thành phố B có độ dài bằng nhau và bằng s (km). Thời gian để đi từ A đến B của tàu hoả là a (giờ), của ô tô khách là b (giờ) (a < b). Tốc độ của tàu hoả gấp bao nhiêu lần tốc độ của ô tô? Tính giá trị này khi s = 350, a = 5, b = 7

Lời giải:

Tốc độ của tàu hỏa: sa (km/h)

Tốc độ của ô tô: sb (km/h)

Tốc độ của tàu hỏa gấp sa:sb=ba lần tốc độ của ô tô

Khi s = 350, a = 5, b = 7, tốc độ của tàu hỏa gấp 75 lần tốc độ của ô tô

Bài tập

Bài tập 1: Thực hiện các phép nhân phân thức sau:

a) $\frac{4y}{3x^2}.\frac{5x^3}{2y^3}$

b) $\frac{x^2-2x+1}{x^2-1}.\frac{x^2+x}{x-1}$

c) $\frac{2x+x^2}{x^2-x+1}.\frac{3x^3+3}{3x+6}$

Lời giải:

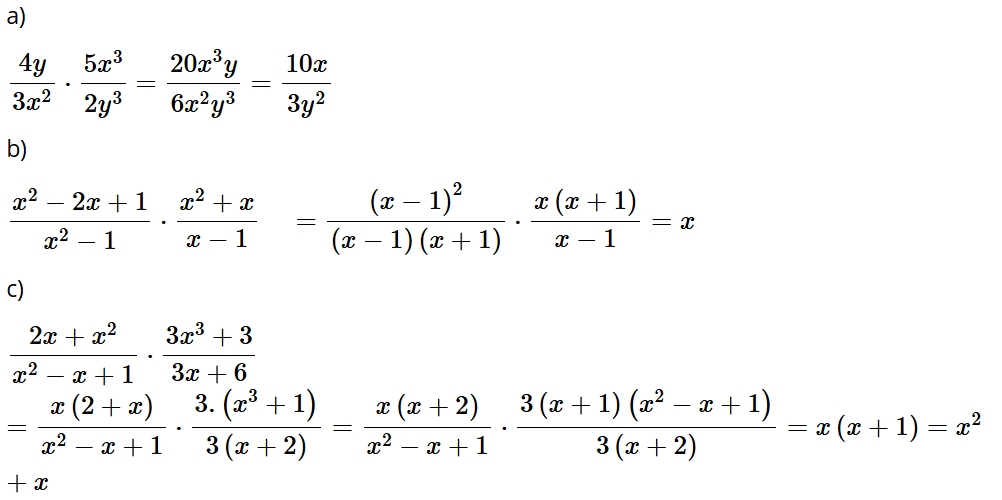
Bài tập 2: Thực hiện các phép chia phân thức sau:

a) $\frac{5x}{4y^3}:\left(-\frac{x^4}{20y}\right)$

b) $\frac{x^2-16}{x+4}:\frac{2x-8}{x}$

c) $\frac{2x+6}{x^3-8}:\frac{{\left(x+3\right)}^3}{2x-4}$

Lời giải:

a) $\frac{5x}{4y^3}:\left(-\frac{x^4}{20y}\right)=\frac{5x}{4y^3}.\frac{-20y}{x^4}=\frac{-25}{x^3{y}^2}$

b) $\frac{x^2-16}{x+4}:\frac{2x-8}{x}=\frac{\left(x+4\right)\left(x-4\right)}{x+4}.\frac{x}{2\left(x-4\right)}=\frac{\left(x-4\right).x}{2\left(x-4\right)}=\frac{x}{2}$

c) $\frac{2x+6}{x^3-8}:\frac{{\left(x+3\right)}^3}{2x-4}=\frac{2\left(x+3\right)}{\left(x-2\right)\left(x^2+2x+4\right)}.\frac{2\left(x-2\right)}{{\left(x+3\right)}^3}$

$=\frac{2\left(x+3\right).2\left(x-2\right)}{\left(x-2\right)\left(x^2+2x+4\right).{\left(x+3\right)}^3}=\frac{4}{\left(x^2+2x+4\right){\left(x+3\right)}^2}$

Bài tập 3: Tính:

a) $\frac{4x^2+2}{x-2}.\frac{3x+2}{x-4}.\frac{4-2x}{2x^2+1}$;

b) $\frac{x+3}{x}.\frac{x+2}{x^2+6x+9}:\frac{x^2-4}{x^2+3x}$.

Lời giải:

a) 4x2+2x−23x+2x−44−2x2x2+1=2(2x2+1)(3x+2)2(2−x)−(2−x)(x−4)(2x2+1)=−4(3x+2)x−4

b) x+3xx+2x2+6x+9:x2−4x2+3x=(x+3)(x+2)x(x+3)x(x+3)2(x−2)(x+2)=1x−2

Bài tập 4: Tính:

a) $\left(\frac{1-x}{x}+x^2-1\right):\frac{x-1}{x};$

b) $\left(\frac{1}{x^2}-\frac{1}{x}\right).\frac{x^2}{y}+\frac{x}{y};$

c) $\frac{3}{x}-\frac{2}{x}:\frac{1}{x}+\frac{1}{x}.\frac{x^2}{3};$

Lời giải:

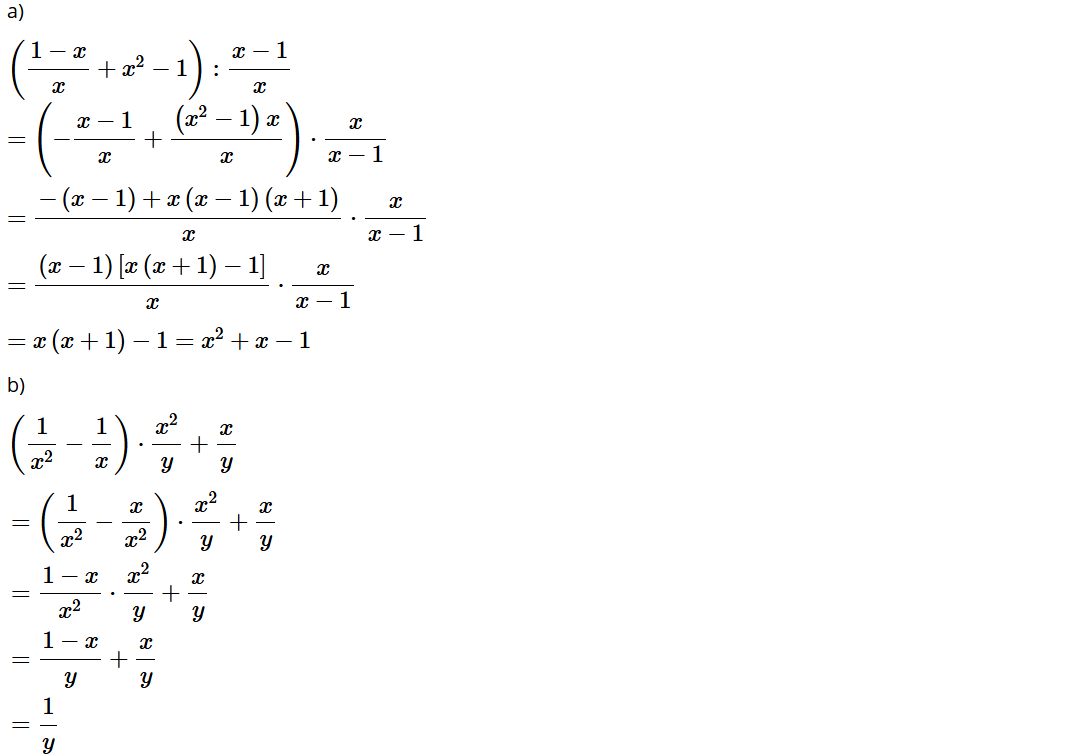
Bài tập 5: Tâm đạp xe từ nhà tới câu lạc bộ câu cá có quãng đường dài 15 km với tốc độ x (km/h). Lượt về thuận chiều gió nên tốc độ nhanh hơn lượt đi 4 km/h

a) Viết biểu thức T biểu thị tổng thời gian hai lượt đi và về.

b) Viết biểu thức t biểu thị hiệu thời gian lượt đi đối với lượt về.

c) Tính T và t với x = 10.

Lời giải:

a) Thời gian lượt đi là: $\frac{15}{x}$ (giờ).

Tốc độ lượt về là: x + 4 (km/h).

Thời gian lượt về là: $\frac{15}{\mathrm{x\; +\; 4}}$ (giờ).

Biểu thức biểu thị tổng thời gian T hai lượt đi và về là:

$T=\frac{15}{x}+\frac{15}{x+4}=\frac{15\left(x+4\right)}{x\left(x+4\right)}+\frac{15.x}{x\left(x+4\right)}$

$=\frac{15x+60+15x}{x\left(x+4\right)}$ = $\frac{30x+60}{x\left(x+4\right)}$ = $\frac{15\left(2x+4\right)}{x\left(x+4\right)}$ (giờ).

b) Biểu thức biểu thị hiệu thời gian t lượt đi đối với lượt về là:

$t=\frac{15}{x}-\frac{15}{x+4}=\frac{15\left(x+4\right)}{x\left(x+4\right)}-\frac{15.x}{x\left(x+4\right)}$

$=\frac{15x+60-15x}{x\left(x+4\right)}=\frac{60}{x\left(x+4\right)}$ (giờ).

c) Xét hai phân thức $T=\frac{30x+60}{x\left(x+4\right)}$ và $t=\frac{60}{x\left(x+4\right)}$.

Điều kiện xác định của hai phân thức trên là x(x + 4) ≠ 0.

Khi x = 10 thì x(x + 4) = 140 ≠ 0 nên điều kiện xác định được thỏa mãn.

Do đó ta có:

$T=\frac{30.10+60}{10.\left(10+4\right)}=\frac{300+60}{10.14}=\frac{360}{140}=\frac{18}{7}$ (giờ).

$t=\frac{60}{10.\left(10+4\right)}=\frac{60}{10.14}=\frac{60}{140}=\frac{3}{7}$ (giờ).