Giải SGK Toán 8 Chân trời sáng tạo Bài 4: Phân tích đa thức thành nhân tử

Khởi động: 

Lời giải:

Ta có: 993 – 99 = 99.(992 – 1)

                          = 99.(992 – 12)

                          = 99.(99 – 1).(99 + 1)

                          = 99.98.100

Do đó 993 – 99 chia hết cho cả ba số 98, 99 và 100.

Ta có: n3 – n = n(n2 – 1)

                     = n.(n – 1).(n + 1)

Do đó n3 – n chia hết cho n, n – 1 và n + 1.

Vậy phát biểu của cả hai bạn đều đúng.

1. Phương pháp đặt nhân tử chung

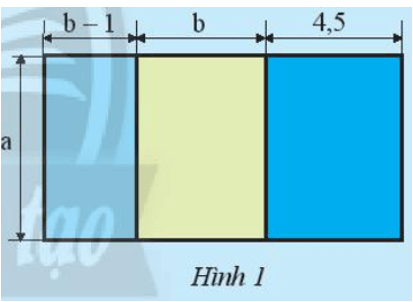
Khám phá 1: Tính diện tích của nền nhà có bản vẽ sơ lược như Hình 1 theo những cách khác nhau, biết a = 5; b = 3,5 (các kích thước tính theo mét).

Tính theo cách nào nhanh hơn?

Lời giải:

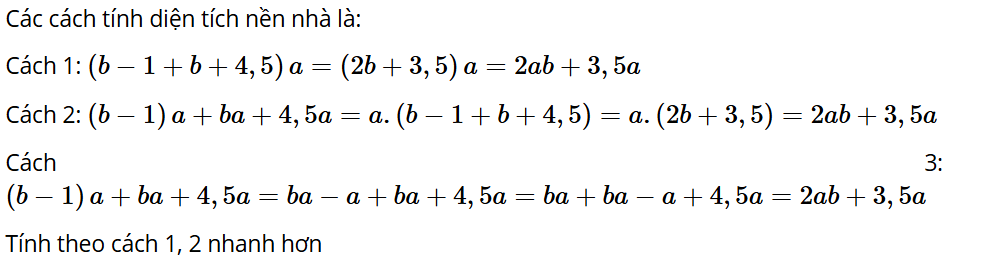
Thực hành 1: Phân tích các đa thức sau thành nhân tử:

a) P = 6x – 2x3;

b) Q = 5x3 – 15x2y;

c) R = 3x3y3 – 6xy3z + xy.

Lời giải:

a) P=6x−2x3=2x×3−2x×x2=2x(3−x2)

b) Q=5x3−15x2y=5x2×x−5x2×3y=5x2(x−3y)

c) R=3x3y3−6xy3z+xy=xy×3x2y2−xy×6y2z+xy=xy(3x2y2−6y2z+1)

2. Phương pháp sử dụng hằng đẳng thức

Khám phá 2: Tìm biểu thức thích hợp thay vào mỗi chỗ , từ đó hoàn thành biến đổi sau vào vở để phân tích đa thức sau thành nhân tử:....

a) $4x^2-9={\left(?\right)}^2-{\left(?\right)}^2=\mathrm{...}$

b) $x^2{y}^2-\frac{1}{4}{y}^2={\left(?\right)}^2-{\left(?\right)}^2=\mathrm{...}$

Lời giải:

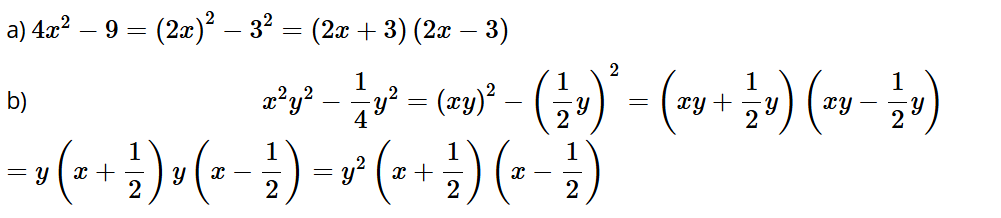
Thực hành 2: Phân tích các đa thức sau thành nhân tử:

a) 9x2 – 16;

b) 4x2 – 12xy + 9y2;

c) t3 – 8;

d) 2ax3y3 + 2a.

Lời giải:

a) 9x2 – 16 = (3x)2 – 42

                  = (3x – 4)(3x + 4).

b) 4x2 – 12xy + 9y2

= (2x)2 – 2.2x.3y + (3y)2

= (2x – 3y)2.

c) t3 – 8 = t3 – 23

              = (t – 2)(t2 + t.2 + 22)

             = (t – 2)(t2 – 2t + 4).

d) 2ax3y3 + 2a

= 2a.(x3y3 + 1)

= 2a.[(xy)3 + 13]

= 2a(xy + 1)[(xy)2 – xy.1 + 12]

= 2a(xy + 1)(x2y2 – xy + 1).

Vận dụng 1: Tìm một hình hộp chữ nhật có thể tích 2x3 – 18x (với x > 3) mà độ dài các cạnh đều là biểu thức chứa x

Lời giải:

Ta có: 2x3−18x=2x(x2−9)=2x(x−3)(x+3)

Độ dài các cạnh của hình hộp chữ nhật cần tìm lần lượt là: 2x, x - 3, x + 3

Vận dụng 2: Giải đáp câu hỏi ở Hoạt động khởi động (trang 23)

Lời giải:

Ta có: 993 – 99 = 99.(992 – 1)

                          = 99.(992 – 12)

                          = 99.(99 – 1).(99 + 1)

                          = 99.98.100

Do đó 993 – 99 chia hết cho cả ba số 98, 99 và 100.

Ta có: n3 – n = n(n2 – 1)

                     = n.(n – 1).(n + 1)

Do đó n3 – n chia hết cho n, n – 1 và n + 1.

Vậy phát biểu của cả hai bạn đều đúng.

3. Phương pháp nhóm hạng tử

Khám phá 3: Hãy hoàn thành biến đổi sau vào vở để phân tích đa thức thành nhân tử:

a2 + ab + 2a + 2b = (a2 + ab) + (2a + 2b) = …

Em có thể biến đổi theo cách khác để phân tích đa thức trên thành nhân tử không?

Lời giải:

Thực hành 3: Phân tích các đa thức sau thành nhân tử:

a) a3 – a2b + a – b;

b) x2 – y2 + 2y – 1.

Lời giải:

a) a3 – a2b + a – b

= (a3 – a2b) + (a – b)

= a2(a – b) + (a – b)

= (a – b)(a2 + 1).

b) x2 – y2 + 2y – 1

= x2 – (y2 – 2y + 1)

= x2 – (y – 1)2

= (x + y – 1).[x – (y – 1)]

= (x + y – 1)(x – y + 1).

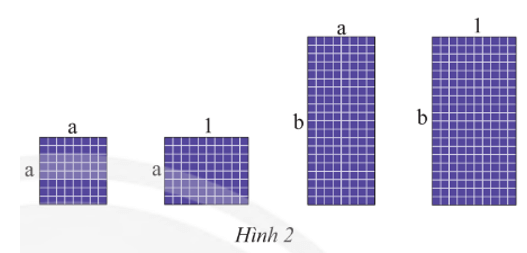
Vận dụng 3: Có thể ghép bốn tấm pin mặt trời với kích thước như Hình 2 thành một hình chữ nhật không? Nếu có, tính độ dài các cạnh và diện tích hình chữ nhật đó. Biết a = 0,8; b = 2 (các kích thước tính theo mét).

Lời giải:

Có thể ghép bốn tấm pin mặt trời thành một hình chữ nhật

Ta có hình chữ nhật có kích thước các cạnh là: a + 1, a + b

Khi a = 0,8, b = 2, kích thước các cạnh là: 1,8 m và 2,8 m

Diện tích hình chữ nhật là: 1,8 x 2,8 = 5,04 (m2)

Bài tập

Bài tập 1: Phân tích các đa thức sau thành nhân tử:

a) x3 + 4x;

b) 6ab – 9ab2;

c) 2a(x – 1) + 3b(1 – x);

d) (x – y)2 – x(y – x).

Lời giải:

a) x3 + 4x = x.x2 + x.4 = x(x2 + 4).

b) 6ab – 9ab2 = 3ab.2 – 3ab.3b = 3ab(2 – 3b).

c) 2a(x – 1) + 3b(1 – x)

= 2a(x – 1) + 3b[– (x – 1)]

= 2a(x – 1) – 3b(x – 1)

= (x – 1)(2a – 3b).

d) (x – y)2 – x(y – x)

= (x – y)2 + x(x – y)

= (x – y)(x – y + x)

= (x – y)(2x – y).

Bài tập 2: Phân tích các đa thức sau thành nhân tử:

a) 4x2 – 1;

b) (x + 2)2 – 9;

c) (a + b)2 – (a – 2b)2.

Lời giải:

a) 4x2−1=(2x)2−1=(2x−1)(2x+1)

b) (x+2)2−9=(x+2)2−32=(x+2−3)(x+2+3)=(x−1)(x+5)

c) (a+b)2−(a−2b)2=(a+b−a+2b)(a+b+a−2b)=3b(2a−b)

Bài tập 3: Phân tích các đa thức sau thành nhân tử:

a) 4a2 + 4a + 1;

b) –3x2 + 6xy – 3y2;

c) (x + y)2 – 2(x + y)z + z2.

Lời giải:

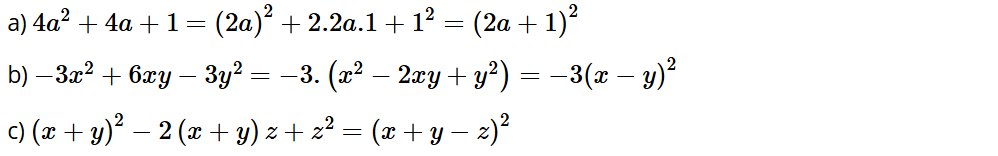
Bài tập 4: Phân tích các đa thức sau thành nhân tử:

a) 8x3 – 1;

b) x3 + 27y3;

c) x3 – y6.

Lời giải:

a) 8x3 – 1

= (2x)3 – 13

= (2x – 1)[(2x)2 + 2x.1 + 12]

= (2x – 1)(4x2 + 2x + 1).

b) x3 + 27y3

= x3 + (3y)3

= (x + 3y)[x2 – x.3y + (3y)2]

= (x + 3y)(x2 – 3xy + 9y2).

c) x3 – y6

= x3 – (y2)3

= (x – y2)[x2 + x.y2 + (y2)2]

= (x – y2)(x2 + xy2 + y4).

Bài tập 5: Phân tích các đa thức sau thành nhân tử:

a) 4x3 – 16x;

b) x4 – y4;

c) xy2 + x2y + $\frac{1}{4}$y3;

d) x2 + 2x – y2 + 1.

Lời giải:

a) 4x3−16x=4x(x2−4)=4x(x−2)(x+2)

b) x4−y4=(x2−y2)(x2+y2)=(x−y)(x+y)(x2+y2)

c) xy2+x2y+14y3=y(xy+x2+14y2)=y(x+12y)2

d) x2+2x−y2+1=(x2+2x+1)−y2=(x+1)2−y2=(x+1−y)(x+1+y)

Bài tập 6: Phân tích các đa thức sau thành nhân tử:

a) x2 – xy + x – y;

b) x2 + 2xy – 4x – 8y;

c) x3 – x2 – x + 1.

Lời giải:

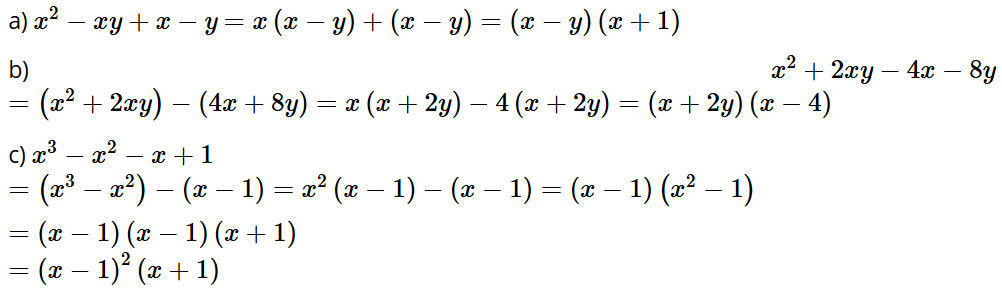
Bài tập 7: Cho y > 0. Tìm độ dài cạnh của hình vuông có diện tích bằng 49y2 + 28y + 4.

Lời giải:

Giả sử hình vuông có độ dài cạnh bằng a (a > 0), khi đó diện tích của hình vuông là a2.

Tức là 49y2 + 28y + 4 = a2.

Ta phân tích đa thức 49y2 + 28y + 4 thành nhân tử có dạng a2.

49y2 + 28y + 4

= (7y)2 + 2.7y.2 + 22

= (7y + 2)2

Vậy độ dài cạnh của hình vuông có diện tích bằng 49y2 + 28y + 4 là 7y + 2.