Giải SGK Toán 11 Kết nối tri thức Bài 19: Lôgarit - Giải SGK Toán 11 - Kết nối tri thức

Mở đầu: Bác An gửi tiết kiệm ngân hàng 100 triệu đồng kì hạn 12 tháng, với lãi suất không đổi là 6% một năm. Khi đó sau n năm gửi thì tổng số tiền bác An thu được (cả vốn lẫn lãi) cho bởi công thức sau:

A = 100 ∙ (1 + 0,06)n (triệu đồng).

Hỏi sau ít nhất bao nhiêu năm, tổng số tiền bác An thu được không dưới 150 triệu đồng?

Lời giải:

Ta có: A = 100 ∙ (1 + 0,06)n = 100 ∙ 1,06n.

Với A = 150, ta có: 100 ∙ 1,06n = 150 hay 1,06n = 1,5, tức là n = log1,06 1,5 ≈ 6,96.

Vì gửi tiết kiệm kì hạn 12 tháng (tức là 1 năm) nên n phải là số nguyên. Do đó ta chọn n = 7.

Vậy sau ít nhất 7 năm thì bác An nhận được số tiền ít nhất là 150 triệu đồng.

1. Khái niệm Lôgarit

Hoạt động 1: Nhận biết khái niệm lôgarit

Tìm x, biết:

a) 2x = 8;

b) $2^{x} = \frac{1}{4}$ ;

c) $2^{x} = \sqrt{2}$ .

Lời giải:

a)log28=3

b)log214=−2.

c)log22–√=12

Luyện tập 1: Tính:

a) $\log_{3} 3 \sqrt{3}$ ;

b) $\log_{\frac{1}{2}} 32$ .

Lời giải:

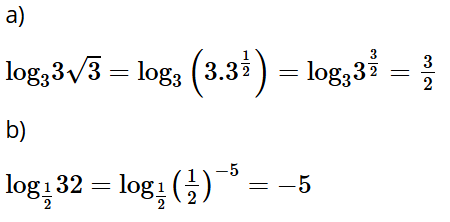
2. Tính chất của Lôgarit

Hoạt động 2: Nhận biết quy tắc tính lôgarit

Cho M = 25, N = 23. Tính và so sánh:

a) log2(MN) và log2M + log2N;

b) $\log_{2} (\frac{M}{N})$ và log2M – log2N.

Lời giải:

a) Ta có log2(MN) = log2(25 ∙ 23) = log2(25 + 3) = log228 = 8

và log2M + log2N = log225 + log223 = 5 + 3 = 8.

Vậy log2(MN) = log2M + log2N.

b) Ta có $\log_{2} (\frac{M}{N}) = \log_{2} (\frac{2^{5}}{2^{3}}) = \log_{2} 2^{5 - 3} = \log_{2} 2^{2} = 2$

và log2M – log2N = log225 – log223 = 5 – 3 = 2.

Vậy $\log_{2} (\frac{M}{N})$ = log2M – log2N.

Luyện tập 2: Rút gọn biểu thức:

A = log2(x3 – x) – log2(x + 1) – log2(x – 1) (x > 1).

Lời giải:

A=log2(x2−x)−log2(x+1)−log2(x−1)=log2x2−x(x+1)(x−1)=xx+1

Biểu thức được rút gọn thành

A=log2xx+1=log2x−log2(x+1)

Hoạt động 3: Xây dựng công thức đổi cơ số của lôgarit

Giả sử đã cho logaM và ta muốn tính logbM. Để tìm mối liên hệ giữa logaM và logbM, hãy thực hiện các yêu cầu sau:

a) Đặt y = logaM, tính M theo y;

b) Lấy lôgarit theo cơ số b cả hai vế của kết quả nhận được trong câu a, từ đó suy ra
công thức mới để tính y.

Lời giải:

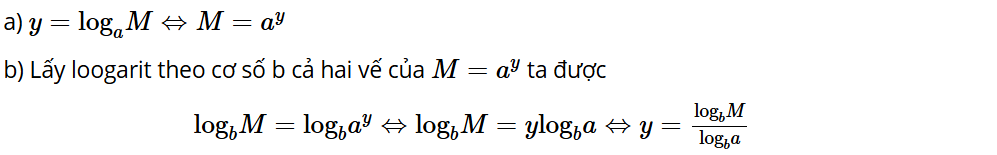
Luyện tập 3: Không dùng máy tính cầm tay, hãy tính $\log_{9} \frac{1}{27}$ .

Lời giải:

Ta có $\log_{9} \frac{1}{27} = \log_{3^{2}} 3^{- 3} = \frac{\log_{3} 3^{- 3}}{\log_{3} 3^{2}} = \frac{- 3}{2}$ .

3. Lôgarit thập phân và Loogarit tự nhiên

Vận dụng: Cô Hương gửi tiết kiệm 100 triệu đồng với lãi suất 6% một năm.

a) Tính số tiền cô Hương thu được (cả vốn lẫn lãi) sau 1 năm, nếu lãi suất được tính theo một trong các thể thức sau:

- Lãi kép kì hạn 12 tháng;

- Lãi kép kì hạn 1 tháng;

- Lãi kép liên tục.

b) Tính thời gian cần thiết để cô Hương thu được số tiền (cả vốn lẫn lãi) là 150 triệu đồng nếu gửi theo thể thức lãi kép liên tục (làm tròn kết quả đến chữ số thập phân thứ nhất).

Lời giải:

Bài tập

Bài 6.9: Tính:

a) log22– 13;

b) $\ln e^{\sqrt{2}}$ ;

c) log816 – log82;

d) log26 ∙ log68.

Lời giải:

a) log22−12=−12log22=−12.

b) lne2√=2–√ln(e)=2–√×1=2–√.

c) log816−log82=log8162=log88=1.

d) log26.log68=log26log26.log68log62=log22.log24log22.log23=log24log23=log34≈1.26186

Bài 6.10: Viết mỗi biểu thức sau thành lôgarit của một biểu thức (giả thiết các biểu thức đều có nghĩa):

a) $A = \ln (\frac{x}{x - 1}) + \ln (\frac{x + 1}{x}) - \ln (x^{2} - 1)$ ;

b) $B = 21 \log_{3} \sqrt[3]{x} + \log_{3} (9 x^{2}) - \log_{3} 9$ .

Lời giải:

a) $A = \ln (\frac{x}{x - 1}) + \ln (\frac{x + 1}{x}) - \ln (x^{2} - 1)$

$= \ln (\frac{x}{x - 1} \cdot \frac{x + 1}{x}) - \ln (x^{2} - 1)$

$= \ln \frac{x + 1}{x - 1} - \ln (x^{2} - 1)$

$= \ln \frac{x + 1}{(x - 1) (x^{2} - 1)}$

$= \ln \frac{x + 1}{(x - 1) (x - 1) (x + 1)}$

$= \ln \frac{1}{{(x - 1)}^{2}} = - \ln {(x - 1)}^{2}$ .

b) $B = 21 \log_{3} \sqrt[3]{x} + \log_{3} (9 x^{2}) - \log_{3} 9$

$= 21 \log_{3} x^{\frac{1}{3}} + \log_{3} (9 x^{2}) - \log_{3} 9$

$= \log_{3} x^{\frac{21}{3}} + \log_{3} (9 x^{2}) - \log_{3} 9$

$= \log_{3} x^{7} + \log_{3} (9 x^{2}) - \log_{3} 9$

$= \log_{3} \frac{x^{7} \cdot 9 x^{2}}{9} = \log_{3} x^{9}$ .

Bài 6.11: Rút gọn các biểu thức sau:

a) $A = \log_{\frac{1}{3}} 5 + 2 \log_{9} 25 - \log_{\sqrt{3}} \frac{1}{5}$ ;

b) $B = \log_{a} M^{2} + \log_{a^{2}} M^{4}$ .

Lời giải:

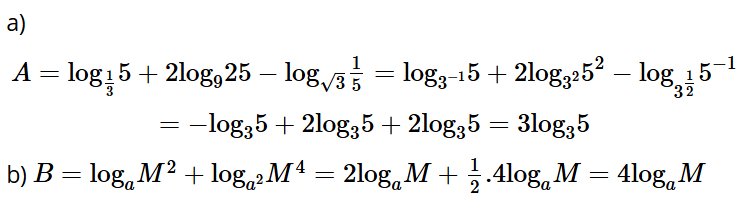
Bài 6.12: Tính giá trị của các biểu thức sau:

a) A = log23 ∙ log34 ∙ log45 ∙ log56 ∙ log67 ∙ log78;

b) B = log22 ∙ log24 ∙∙∙ log22n.

Lời giải:

a) Áp dụng công thức đổi cơ số, ta có:

A = log23 ∙ log34 ∙ log45 ∙ log56 ∙ log67 ∙ log78

$= \frac{\log 3}{\log 2} \cdot \frac{\log 4}{\log 3} \cdot \frac{\log 5}{\log 4} \cdot \frac{\log 6}{\log 5} \cdot \frac{\log 7}{\log 6} \cdot \frac{\log 8}{\log 7}$

$= \frac{\log 8}{\log 2} = \log_{2} 8 = \log_{2} 2^{3} = 3$ .

b) B = log22 ∙ log24 ∙∙∙ log22n

= log22 ∙ log222 ∙∙∙ log22n

= 1 ∙ 2 ∙ … ∙ n = n!.

Bài 6.13: Biết rằng khi độ cao tăng lên, áp suất không khí sẽ giảm và công thức tính áp suất dựa trên độ cao là

a = 15 500(5 – log p),

trong đó a là độ cao so với mực nước biển (tính bằng mét) và p là áp suất không khí (tính bằng pascal).

Tính áp suất không khí ở đỉnh Everest có độ cao 8 850 m so với mực nước biển.

Lời giải:

Để tính áp suất không khí ở độ cao 8.850m, ta thay a = 8.850 vào công thức và giải phương trình để tìm giá trị của p.

Ta có:

a = 15.500(5 - log p)

8.850 = 15.500(5 - log p)

5 - log p = 8.85015.500

log p =5−8.85015.500

log p = 3.407

p=103.407≈245,37Pa

Vậy áp suất không khí ở độ cao 8.850m so với mực nước biển là khoảng 245,37 Pa.

Bài 6.14: Mức cường độ âm L đo bằng decibel (dB) của âm thanh có cường độ I (đo bằng oát trên mét vuông, kí hiệu là W/m2) được định nghĩa như sau:

$L (I) = 10 \log \frac{I}{I_{0}}$ ,

trong đó I0 = 10– 12 W/m2 là cường độ âm thanh nhỏ nhất mà tai người có thể phát hiện được (gọi là ngưỡng nghe).

Xác định mức cường độ âm của mỗi âm sau:

a) Cuộc trò chuyện bình thường có cường độ I = 10– 7 W/m2.

b) Giao thông thành phố đông đúc có cường độ I = 10– 3 W/m2.

Lời giải: