Giải SGK Toán 11 Kết nối tri thức Bài 22: Hai đường thẳng vuông góc - Giải SGK Toán 11 - Kết nối tri thức

1. Góc giữa hai đường thẳng

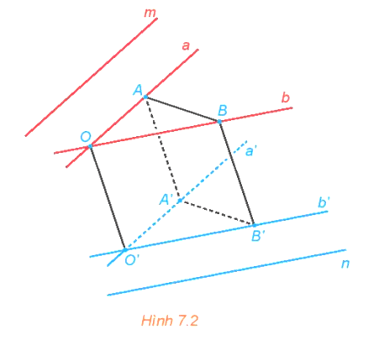
Hoạt động 1: Trong không gian, cho hai đường thẳng chéo nhau m và n. Từ hai điểm phân biệt O, O' tuỳ ý lần lượt kẻ các cặp đường thẳng a, b và a', b' tương ứng song song với m, n (H.7.2).

a) Mỗi cặp đường thẳng a, a' và b, b' có cùng thuộc một mặt phẳng hay không?

b) Lấy các điểm A, B (khác O) tương ứng thuộc a, b. Đường thẳng qua A song song với OO' cắt a' tại A', đường thẳng qua B song song với OO' cắt b' tại B'. Giải thích vì sao OAA'O'; OBB'O'; ABB'A' là các hình bình hành.

c) So sánh góc giữa hai đường thẳng a, b và góc giữa hai đường thẳng a', b'.

(Gợi ý: Áp dụng định lí côsin cho các tam giác OAB, O'A'B' ).

HĐ1 trang 28 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

Lời giải:

Câu hỏi: Nếu a song song hoặc trùng với a' và b song song hoặc trùng với b' thì (a, b) và (a', b') có mối quan hệ gì?

Lời giải:

- Nếu a song song hoặc trùng với a' và b song song hoặc trùng với b' thì (a, b) = (a', b').

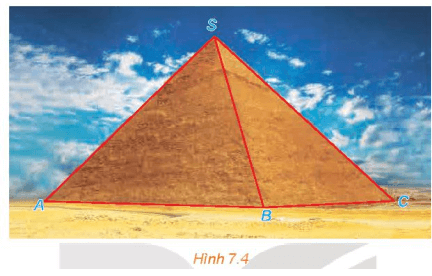
Vận dụng: Kim tự tháp Kheops là kim tự tháp lớn nhất trong các kim tự tháp ở Ai Cập, được xây dựng vào thế kỉ thứ 26 trước Công nguyên và là một trong bảy kì quan của thế giới cổ đại. Kim tự tháp có dạng hình chóp với đáy là hình vuông có cạnh dài khoảng 230 m, các cạnh bên bằng nhau và dài khoảng 219 m (kích thước hiện nay).

(Theo britannica.com).

Tính (gần đúng) góc tạo bởi cạnh bên SC và cạnh đáy AB của kim tự tháp

Vận dụng trang 29 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

Lời giải:

Xét tam giác vuông ASC

Với AC là độ dài đường chéo của đáy kim tự tháp, ta có:

AC=AB2–√≈325.27m

Theo pytago ta có:

AS2=AC2−SC2≈325.272−2192≈124108,44

AS=124108.44−−−−−−−−√≈352.24m

Góc tạo bởi cạnh bên SC và cạnh đáy AB bằng cách sử dụng định lý sin trong tam giác vuông ASC:

sin(ASC^)=SCAC=219325.27≈0.6736

⇒ASC^≈arcsin(0.6736)≈42,79∘

Vậy góc tạo bởi cạnh bên SC và cạnh đáy AB của kim tự tháp Cheops là khoảng 42.79∘ .

2. Hai đường thẳng vuông góc

Hoạt động 2: Đối với hai cánh cửa trong Hình 7.5, tính góc giữa hai đường mép cửa BC và MN.

HĐ2 trang 29 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

Lời giải:

Vì BC // PN nên (BC, MN) = (PN, MN)

Mà PN vuông góc với MN nên góc giữa hai đường mép này bằng 90⁰

Câu hỏi: Nếu đường thẳng a vuông góc với đường thẳng b thì a có vuông góc với các đường thẳng song song với b hay không?

Lời giải:

Vì a ⊥ b nên (a, b) = 90° mà b // c nên (a, b) = (a, c) = 90°. Vậy a ^ c.

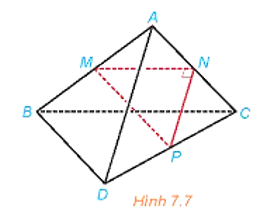
Luyện tập: Cho tam giác MNP vuông tại N và một điểm A nằm ngoài mặt phẳng (MNP). Lần lượt lấy các điểm B, C, D sao cho M, N, P tương ứng là trung điểm của AB, AC, CD (H.7.7). Chứng minh rằng AD và BC vuông góc với nhau và chéo nhau.

Luyện tập trang 30 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

Lời giải:

Xét tam giác ABC có M là trung điểm của AB, N là trung điểm của AC nên MN là đường trung bình của tam giác ABC, suy ra MN // BC.

Xét tam giác ACD có N là trung điểm của AC, P là trung điểm của CD nên NP là đường trung bình của tam giác ACD, suy ra NP // AD.

Khi đó (AD, BC) = (NP, MN) = $\hat{M N P}$ .

Do tam giác MNP vuông tại N nên $\hat{M N P} = 90 °$ .

Vậy AD và BC vuông góc với nhau.

Nếu D ∈ (ABC) thì A ∈ (MNP) (vô lí).

Do đó D ∉ (ABC) nên AD và BC chéo nhau.

Bài tập

Bài 7.1: Cho hình lăng trụ ABC.A'B'C' có đáy là các tam giác đều. Tính góc (AB, B'C').

Lời giải:

Bài 7.2: Cho hình hộp ABCD.A'B'C'D' có các cạnh bằng nhau. Chứng minh rằng tứ diện ACB'D' có các cặp cạnh đối diện vuông góc với nhau.

Lời giải:

Gọi O là trung điểm của AC, khi đó ta có:

AB' = AO + OB'

CD' = CO + OD'

Vì AB' và CD' có cùng độ dài và vuông góc với AC nên chúng cũng cùng vuông góc với nhau nếu và chỉ nếu:

AB' · CD' = 0

Ta có:

AB' · CD' = (AO + OB') · (CO + OD')
= AO · CO + AO · OD' + OB' · CO + OB' · OD'
Vì AO = CO, OB' = OD' và AB' // CD', nên ta có: AO · OD' = CO · OB' = 0
=> AB' · CD' = 0

Vậy ta đã chứng minh được rằng tứ diện ACB'D' có các cặp cạnh đối diện vuông góc với nhau.

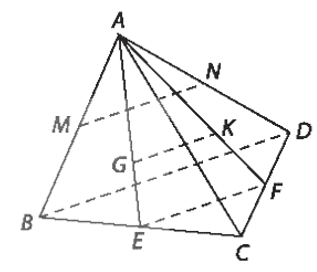
Bài 7.3: Cho tứ diện ABCD có $\hat{C B D} = 90 °$ .

a) Gọi M, N tương ứng là trung điểm của AB, AD. Chứng minh rằng MN vuông góc với BC.

b) Gọi G, K tương ứng là trọng tâm của các tam giác ABC, ACD. Chứng minh rằng GK vuông góc với BC.

Lời giải:

Bài 7.3 trang 30 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

a) Xét tam giác ABD, có M là trung điểm của AB, N là trung điểm của AD nên MN là đường trung bình của tam giác ABD, suy ra MN // BD.

Khi đó (MN, BC) = (BD, BC) = $\hat{C B D} = 90 °$ .

Vậy MN vuông góc với BC.

b) Gọi AG cắt BC tại E, suy ra E là trung điểm BC, AK cắt CD tại F, suy ra F là trung điểm CD.

Vì G là trọng tâm tam giác ABC nên $\frac{A G}{A E} = \frac{2}{3}$ , K là trọng tâm tam giác ACD nên $\frac{A K}{A F} = \frac{2}{3}$ .

Xét tam giác AEF có $\frac{A G}{A E} = \frac{A K}{A F} = \frac{2}{3}$ nên GK // EF.

Xét tam giác BCD có E, F lần lượt là trung điểm của BC, CD nên EF là đường trung bình, suy ra EF // BD.

Vì GK // EF và EF // BD nên GK // BD mà BD ⊥ BC nên GK ⊥ BC.

Bài 7.4: Đối với nhà gỗ truyền thống, trong các cấu kiện: hoành, quá giang, xà cái, rui, cột tương ứng được đánh số 1, 2, 3, 4, 5 như trong Hình 7.8, những cặp cấu kiện nào vuông góc với nhau?

Bài 7.4 trang 30 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

Lời giải:

Trong nhà gỗ truyền thống, các cấu kiện thường được lắp ráp với nhau bằng các mối ghép chéo, do đó các cặp cấu kiện vuông góc với nhau là:

+ Hoành (1) và quá giang (2).

+ Xà cái (3) và cột (5).

+ Quá giang (2) và rui (4).