Giải SGK Toán 11 Kết nối tri thức Bài 27: Thể tích

Hoạt động 1: Khi mua máy điều hòa, bác An được hướng dẫn rằng mỗi mét khối của phòng cần công suất điều hòa 200 BTU. Căn phòng bác An cần lắp máy có dạng hình hộp chữ nhật, rộng 4m, dài 5m và cao 3m. Hỏi bác An cần mua loại điều hòa có công suất bao nhiêu BTU?

Lời giải:

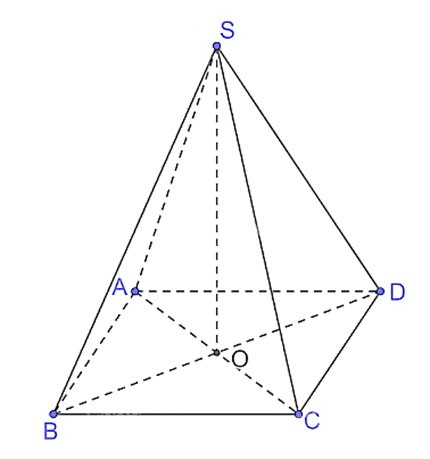
Luyện tập 1: Cho khối chóp đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng b. Tính thể tích của khối chóp.

Lời giải:

Gọi O là giao điểm của AC và BD. Vì S.ABCD là hình chóp đều nên SO $\perp$ (ABCD).

Xét tam giác BCD vuông tại C, có BD = $\sqrt{B{C}^2+C{D}^2}=\sqrt{a^2+a^2}=a\sqrt{2}$ .

Vì ABCD là hình vuông nên O là trung điểm của BD, suy ra BO = $\frac{BD}{2}=\frac{a\sqrt{2}}{2}$ .

Xét tam giác SOB vuông tại O, có SO = $\sqrt{S{B}^2-O{B}^2}=\sqrt{b^2-\frac{a^2}{2}}$ .

Ta có $V_{S.ABCD}=\frac{1}{3}\cdot S_{ABCD}\cdot SO$$=\frac{1}{3}\cdot a^2\cdot \sqrt{b^2-\frac{a^2}{2}}$$=\frac{1}{3}\cdot a^2\cdot \sqrt{\frac{2b^2-a^2}{2}}$

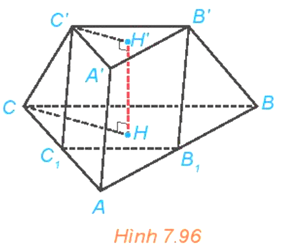
Luyện tập 2: Cho khối chóp cụt đều ABC.A'B'C' có đường cao HH' = h, hai mặt đáy ABC, A'B'C' có cạnh tương ứng bằng 2a, a.

a)Tính thể tích khối chóp cụt.

b) Gọi B1, C1 tương ứng là trung điểm AB, AC. Chứng minh rằng AB1C1.A'B'C' là một hình lăng trụ. Tính thể tích khối lăng trụ AB1C1.A'B'C'.

Lời giải:

a) Thể tích của khối chóp cụt là:

V=13⋅2a2⋅h=23a2h

b) Ta có B1C1−→−−=12AB−→−+12AC−→−=12BC−→− 

Để tính thể tích của khối lăng trụ, ta sử dụng công thức:

V=Sđáy⋅h

Trong đó, Sđáy là diện tích đáy của lăng trụ. Ta có:

Sđáy =12⋅2a⋅2a=2a2

Chiều cao của lăng trụ bằng chiều cao của khối chóp cụt, do đó thể tích của khối lăng trụ là:

V=2a2⋅h

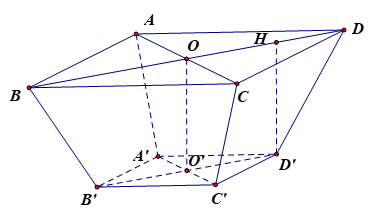
Vận dụng: Một sọt đựng đồ có dạng hình chóp cụt đều (H.7.98). Đáy và miệng sọt là các hình vuông tương ứng có cạnh bằng 30 cm, 60 cm, cạnh bên của sọt dài 50 cm. Tính thể tích của sọt.

Lời giải:

Sọt đựng đồ có dạng hình chóp cụt đều ABCD.A'B'C'D'.

Ta có S1 = SABCD = 602 = 3 600(cm2), S2 = SA'B'C'D' = 302 = 900 (cm2).

Kẻ D'H $\perp$ BD tại H.

Gọi O và O' lần lượt là tâm của hình vuông ABCD và A'B'C'D'.

Vì OO' $\perp$ (ABCD) nên OO' $\perp$ OH, OO' $\perp$ (A'B'C'D') nên OO' ^ B'D'.

Do đó OHD'O' là hình chữ nhật, suy ra O'D' = OH, OO' = HD'.

Xét tam giác B'C'D' vuông tại C', có

B'D' = $\sqrt{B^{\prime }{C^{\prime }}^2+C^{\prime }{D^{\prime }}^2}=\sqrt{{30}^2+{30}^2}=30\sqrt{2}$ (cm).

Vì O' là trung điểm của B'D' nên D'O' = $\frac{D\text{'}B\text{'}}{2}$ = 15$\sqrt{2}$ (cm).

Xét tam giác BCD vuông tại C, có

BD = $\sqrt{B{C}^2+C{D}^2}=\sqrt{{60}^2+{60}^2}=60\sqrt{2}$ (cm).

Mà O là trung điểm của BD nên DO = $\frac{DB}{2}$= 30$\sqrt{2}$ (cm).

Có HD = DO – OH = 30$\sqrt{2}$-15$\sqrt{2}$ = 15$\sqrt{2}$ (cm).

Xét tam giác DHD' vuông tại H, có

D'H = $\sqrt{2^{}-H{D}^2}=\sqrt{{50}^2-{\left(15\sqrt{2}\right)}^2}=5\sqrt{82}$ (cm).

Do đó OO' = 5$\sqrt{82}$ (cm).

$V_{ABCD.A^{\prime }{B}^{\prime }{C}^{\prime }D}=\frac{1}{3}\left(S_1+S_2+\sqrt{S_1\cdot S_2}\right)\cdot$

$=\frac{1}{3}\left(3600+900+\sqrt{3600\cdot 900}\right)\cdot 5\sqrt{82}$ = 10500$\sqrt{82}$ (cm3).

Bài tập

Bài 7.28: Cho khối chóp đều S.ABC, đáy có cạnh bằng a, cạnh bên bằng b. Tính thể tích của khối chóp đó. Từ đó suy ra thể tích của khối tứ diện đều có cạnh bằng a.

Lời giải:

Bài 7.29: Cho khối lăng trụ đứng ABC.A'B'C' có AA' = 5 cm, AB = 6 cm, BC = 2 cm, ${\mathrm{ABC^\backslash widehat\{ABC\}ABC}}^{}=150°$ . Tính thể tích của khối lăng trụ.

Lời giải:

Vì ABC.A'B'C' là khối lăng trụ đứng nên A'A $\perp$ (ABC).

Có SABC = $\frac{1}{2}$.AB.AC.sin${\mathrm{ABC^\backslash widehat\{ABC\}ABC}}^{}$ = $\frac{1}{2}$.6.2.sin150o = 3 (cm2).

$V_{ABC.A^{\prime }{B}^{\prime }{C}^{\prime }}=S_{ABC}$.AA' = 3 . 5 = 15 (cm3).

Bài 7.30: Cho khối chóp đều S.ABCD, đáy có cạnh 6 cm. Tính thể tích của khối chóp đó trong các trường hợp sau:

a) Cạnh bên tạo với mặt đáy một góc bằng 60°.

b) Mặt bên tạo với mặt đáy một góc bằng 45°.

Lời giải:

a) Thể tích của khối chóp theo công thức :

V=13Sday.h=13.3√4.2.6=363–√cm3

b) Công thức tính thể tích của khối chóp, ta có:

V=13Sday.h=13.14.62.h=3hcm3

Mà Trong đó BDCˆ=45∘ và b=c, do đó b=623−−√

Ta sẽ tính chiều cao h bằng cách sử dụng định lí Pytago trong tam giác BDC:

h2=BD2−(b2)2=(62√23√)2=6

Vậy thể tích của khối chóp là 3h=36–√ cm3.

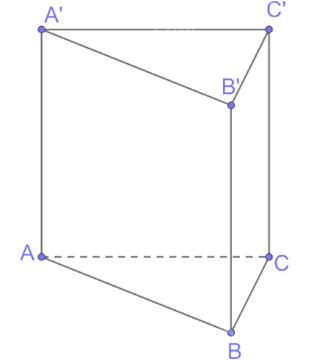
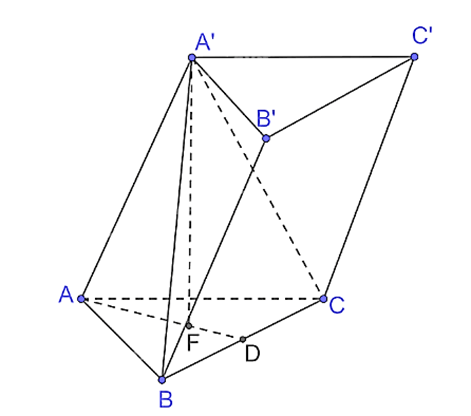
Bài 7.31: Cho khối lăng trụ ABC.A'B'C' có đáy là các tam giác đều cạnh a, A'A = A'B = A'C = b. Tính thể tích của khối lăng trụ.

Lời giải:

Vì hình chóp A'.ABC có A'A = A'B = A'C, ABC là tam giác đều nên hình chóp A'.ABC là hình chóp đều.

Gọi F là hình chiếu của A' trên mặt phẳng (ABC), khi đó F là trọng tâm tam giác ABC. Khi đó A'F $\perp$ (ABC) hay A'F là đường cao của hình lăng trụ ABC.A'B'C'.

Giả sử AF $\cap$ CB tại D, suy ra D là trung điểm của BC, AD $\perp$ BC.

Vì ABC là tam giác đều cạnh a, đường cao AD nên AD = $\frac{a\sqrt{3}}{2}$ và SABC = $\frac{a^2\sqrt{3}}{4}$ .

Có AF = $\frac{2}{3}$AD = $\frac{2}{3}$.$\frac{a\sqrt{3}}{2}$=$\frac{a\sqrt{3}}{3}$.

Xét tam giác A'FA vuông tại F, có

A'F = $\sqrt{A{A^{\prime }}^2-A{F}^2}=\sqrt{b^2-\frac{a^2}{3}}=\sqrt{\frac{3b^2-a^2}{3}}$.

Khi đó $V_{ABC.A^{\prime }{B}^{\prime }{C}^{\prime }}=S_{ABC}\cdot A^{\prime }F$$=\frac{a^2\sqrt{3}}{4}\cdot \sqrt{\frac{3b^2-a^2}{3}}$$=\frac{a^2\sqrt{3b^2-a^2}}{4}$ .

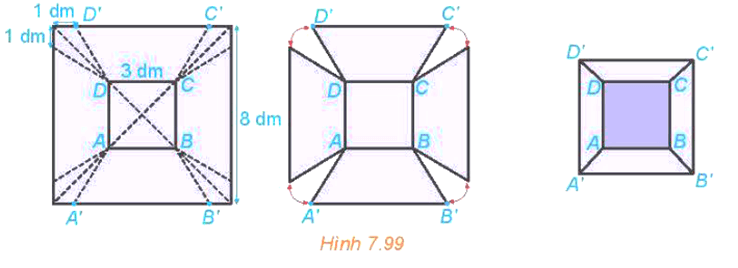
Bài 7.32: Từ một tấm tôn hình vuông có cạnh 8 dm, bác Hùng cắt bỏ bốn phần như nhau ở bốn góc, sau đó bác hàn các mép lại để được một chiếc thùng (không có nắp) như Hình 7.99.

a) Giải thích vì sao chiếc thùng có dạng hình chóp cụt.

b) Tính cạnh bên của thùng.

c) Hỏi thùng có thể chứa được nhiều nhất bao nhiêu lít nước?

Lời giải: